Случайные величины и их характеристики
Внезапные отказы определяются случайными неблагоприятными сочетаниями нескольких факторов. Случайность связана с тем, что причины события остаются для нас скрытыми.
Разброс ресурсов по критерию усталости (оценивается отношением наибольшего ресурса к наименьшему его значению) для подшипников достигает 40, для зубчатых передач от 10 до 15. Разброс ресурсов по износу также весьма значительно. Существенный разброс имеют действующие нагрузки, механические характеристики материалов и деталей, зазоры и натяги, которые при изготовлении получаются как разности сопрягаемых размеров.
Поэтому в расчетах надежности многие параметры должны рассматриваться случайными величинами, которые могут принять то или иное значение, неизвестное заранее. Они могут быть непрерывного или дискретного типа.
Для каждого числа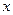 
в диапазоне изменения случайной величины 
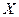существует определенная вероятность 
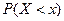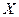, что не превосходит 
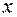. Эта зависимость 
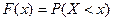называется функцией распределения или функцией вероятности случайной величины .
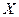Функция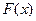 
является неубывающей функцией 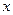. В пределах изменения случайной величины 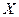она изменяется от 0 до 1.
Производная от функции распределения по текущей переменной
,
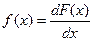называется плотностью распределения. Она характеризует частоту повторения данного значения случайной величины. В задачах надежности она широко используется как плотность вероятности.
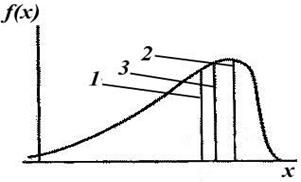
Рисунок 1.3 - Плотность вероятности и числовые характеристики центра группирования случайной величины: 1 – медиана; 2 – мода;
3 – математическое ожидание
В ряде случаев достаточно характеризовать распределение случайной величины некоторыми числовыми величинами (рисунок 1.3):
- математическим ожиданием (средним значением),
- модой и медианой, которые характеризуют положение центров группирования случайных величин по числовой оси,
- дисперсией, средним квадратичным отклонением, коэффициентом вариации, которые характеризуют рассеяние случайной величины.
Характеристики распределений используются в статистической трактовке (для обработки результатов наблюдений) и в вероятностной трактовке (для прогнозирования надежности).
Математическое ожидание (среднее значение)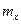 
– основная и простейшая характеристика случайной величины 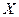. Значение математического ожидания, определяемое по результатам наблюдений, как для дискретных, так и для непрерывных величин, называют оценкой математического ожидания или оценкой среднего значения 
:
,
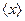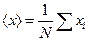где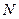 
– общее число наблюдений; 
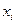– значение случайной величины.
При достаточно большом числе наблюдений (испытаний) полагают, что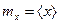 
.
В вероятностных задачах математическое ожидание определяют в зависимости от плотности распределения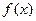 
:
.
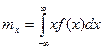Дисперсия случайной величины – математическое ожидание квадрата отклонения этой величины от ее математического ожидания. Оценка дисперсии случайной величины – среднее значение квадрата разности между значениями случайной величины и ее средним значением:
.
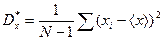Слово «дисперсия» означает рассеяние и характеризует разброс случайной величины.
Для случайных непрерывных величин
.
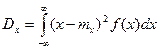Дисперсия имеет размерность квадрата случайной величины. Так как удобнее пользоваться характеристикой разброса, имеющей ту же размерность, что и случайная величина, то была введена характеристика – среднее квадратичное отклонение, представляющее собой корень квадратный из дисперсии:
.
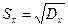Для оценки рассеяния с помощью безразмерной (относительной) величины используют коэффициент вариации, равный отношению среднего квадратичного отклонения к математическому ожиданию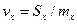 
.
Квантилю называют значение случайной величины, соответствующее заданной вероятности.
Квантиль, соответствующая вероятности 0,5, называется медианой. Медиана характеризует расположение центра группирования случайной величины. Площадь под графиком функции плотности распределения делится медианой пополам.
Модой случайной величины называется ее наиболее вероятное значение, то ее значение, при котором плотность вероятности максимальна.
Для симметричного модального (т. е. имеющего один максимум) распределения математическое ожидание, мода и медиана совпадают.
Оценки. Характеристики распределений, параметры надежности используются в статистической трактовке для оценки состояния и в математической теории надежности называют оценками. При достаточно большом количестве испытаний они принимаются за истинные характеристики надежности.
В вероятностной трактовке для прогнозирования.
Рассмотрим проведенные для оценки надежности испытания или эксплуатацию значительного числа 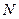элементов в течение времени 
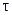. Пусть к концу испытания или срока эксплуатации останется 
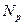работоспособных (не отказавших) элементов и 
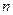отказавших.
Тогда относительное количество отказов
.
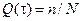Если испытание проводится как выборочное, то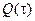 
можно рассматривать как статистическую оценку вероятности отказа или, если 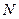достаточно велико, как вероятность отказа.
Вероятность безотказной работы оценивается относительным количеством работоспособных элементов
.
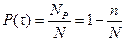Так как безотказная работа и отказ – взаимно противоположные события, то сумма их вероятностей равна 1:
.
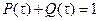Это же следует из приведенных выше зависимостей.
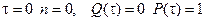При 
. При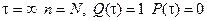 
.
Распределение отказов по времени характеризуется функцией плотности распределения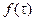 
наработки до отказа
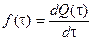
Вероятности отказов и безотказной работы в функции плотность 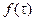выражаются зависимостями
;
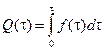при условии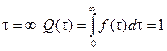 
; 
.
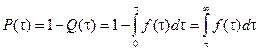Интенсивность отказов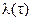 
в отличие от плотности распределения относится к числу объектов 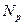, оставшихся работоспособными, а не к общему числу объектов. Учитывая, что 
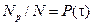, получим
.
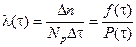Если в данное выражение подставим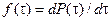 
, разделим переменные и произведем интегрирование Выражение для вероятности безотказной работы в зависимости от интенсивности отказов получим,:
; 
; 
.
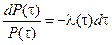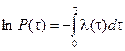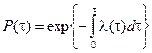Это соотношение является одним из основных уравнений теории надежности.
Вероятность безотказной работы нужно уметь определять для любого промежутка времени. По теореме умножения вероятностей
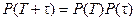или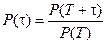 
,
где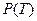 
и 
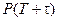– вероятности безотказной работы за время 
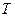и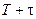 
соответственно; 
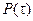– условная вероятность безотказной работы за время 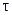. Термин «условная» здесь введен, поскольку вероятность определяется в предположении, что изделия не имели отказа до начала интервала времени или наработки.