Электродвижущая сила. Закон Ома для неоднородного участка цепи. Закон Кирхгофа

Мы рассматривали закон Ома (98.1) для однородного участка цепи, т. е. такого, в котором не действует ЭДС (не действуют сторонние силы). Теперь рассмотрим неоднородный участок цепи.

Если ток проходит по неподвижным проводникам, образующим участок 1—2,то работа А₁₂ всех сил (сторонних и электростатических), совершаемая над носителями тока, по закону сохранения и превращения энергии равна теплоте, выделяющейся на участке. Работа сил, совершаемая при перемещении заряда Q₀ на участке 1—2, согласно (97.4), А₁₂=Q₀ E₀+Q₀( )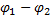

ЭДС E₁₂, как и сила тока /, — величина скалярная. Ее необходимо брать либо с положительным, либо с отрицательным знаком в зависимости от знака работы, совершаемой сторонними силами. Если ЭДС способствует движению положительных зарядов в выбранном направлении (в направлении 1 — 2), то E₁₂ > 0. Если ЭДС препятствует движению положительных зарядов в данном направлении, то E₁₂ < 0.

За время t в проводнике выделяется теплота Q = pRt = IR(It) = IRQ₀.

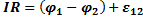(1) откуда 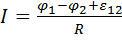(4)

Выражение (1) или (2) представляет собой закон Ома для неоднородного участка цепи в интегральной форме, который является обобщенным законом Ома.

Если на данном участке цепи источник тока отсутствует (E₁₂=0), то из (4) приходим к закону Ома для однородного участка цепи (98.1): I = Ф1-Ф2/R = U/R

Если же электрическая цепь замкнута, то выбранные точки 1 и 2 совпадают, ф₁ = ф₂

тогда из (4) получаем закон Ома для замкнутой цепи: I=E/r + R₁

Расчет разветвленных цепей значительно упрощается, если пользоваться правилами, сформулированными немецким физиком Г. Р. Кирхгофом. Этих правил два.

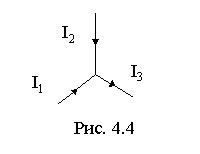
Первое из них относится к узлам цепи. Узлом называется точка, в которой сходится более чем два проводника (рис. 4.4). Ток, текущий к узлу, считается положительным, текущий от узла имеет противоположный знак. Первое правило Кирхгофа гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю: .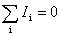

Это правило вытекает из уравнения непрерывности, т. е., в конечном счете, из закона сохранения заряда. Число уравнений, составленных по первому правилу Кирхгофа, должно быть на одно меньше, чем число узлов в исследуемой цепи. Этим обеспечивается линейная независимость получаемых уравнений.

Второе правило относится к любому выделенному в разветвленной цепи замкнутому контуру (например, 1-3-2) (см. рис. 4.5). Зададим направление обхода, изобразив его стрелкой. Применим к каждому из неразветвленных участков контура закон Ома: ; .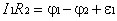

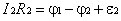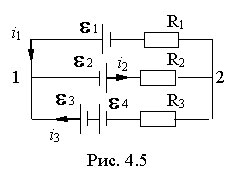При сложении этих выражений получается одно из уравнений ;
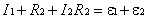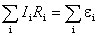
которое выражает второе правило Кирхгофа: для любого замкнутого контура алгебраическая сумма всех падений напряжения равна сумме всех ЭДС в этом контуре.

Подобные уравнения могут быть составлены для всех замкнутых контуров, сущ. в данной разветвленной цепи, однако их число должно быть ограничено уравнениями для независимых контуров, в которых встречается хотя бы один ток, не входящий в остальные.
При составлении уравнений согласно 2-му правилу Кирхгофа токам и ЭДС нужно приписывать знаки в соответствии с выбранным направлением обхода.
Например, ток 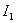нужно считать «+», он течет по направлению обхода. ЭДС 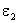также нужно приписать знак "плюс", так как она действует в направлении обхода. Току 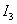и ЭДС 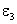приписывается знак "минус".
На практике, при решении задач, при составлении уравнений направления токов выбирают произвольно и в соответствии с этим применяют правило знаков.
Действительное направление токов определится решением задачи: если какой-либо ток окажется положительным, то его направление выбрано правильно, если отрицательным, то в действительности он течет противоположно выбранному направлению. Число независимых уравнений, составленных в соответствии с первым и вторым правилами Кирхгофа, равно числу различных токов, текущих в разветвленной цепи. Поэтому, если заданы ЭДС и сопротивления, то могут быть вычислены все токи.

Если в цепи на носители тока действуют только силы электростатического поля, то происходит перемещение носителей (они предполагаются положительными) от точек с большим потенциалом к точкам с меньшим потенциалом. Это приводит к выравниванию потенциалов во всех точках цепи и к исчезновению электрического поля. Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками тока. Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними.

Природа сторонних сил может быть различной. Например, в гальванических элементах они возникают за счет энергии химических реакций между электродами и электролитами; в генераторе — за счет механической энергии вращения ротора генератора и т. п. Роль источника тока в электрической цепи,

образно говоря, такая же, как роль насоса, который необходим для перекачивания жидкости в гидравлической системе. Под действием создаваемого поля сторонних сил электрические за ряды движутся внутри источника тока против сил электростатического поля, благодаря чему на концах цепи поддер-

живается разность потенциалов и в цепи течет постоянный электрический ток.

Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (ЭДС), действующей в цепи: (97.1)

Эта работа производится за счет энергии, затрачиваемой в источнике тока, поэтому величину E можно также называть электродвижущей силой источника тока, включенного в цепь. Часто, вместо того чтобы сказать: «в цепи действуют сторонние силы», говорят: «в цепи действует ЭДС», т.е. термин «электродвижущая сила» употребляется как характеристика сторонних сил. ЭДС, как и потенциал, выражается в вольтах. Сторонняя сила F_CT, действующая на заряд Q_o, может быть выражена как где Ест — напряженность поля сторонних сил. Работа сторонних сил по перемещению заряда Q_o на замкнутом участке цепи

Разделив (97.2) на Qo, получим выражение для ЭДС, действующей в цепи:

т.е. ЭДС, действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности поля сторонних сил. ЭДС, действующая на участке 1 — 2, равна (97.3)

На заряд Q₀ помимо сторонних сил действуют также силы электростатического поля Fe = Q₀E. Таким образом, результирующая сила, действующая в цепи на заряд Qo, равна F = F_CT + F_c = Q₀(E_CT + Е).

Работа, совершаемая результирующей силой над зарядом Q₀ на участке 1 — 2, равна

Используя выражения (97.3) и(84.8), можем записать

Для замкнутой цепи работа электростатических сил равна нулю (см. §83), поэтому в данном случае А₁₂=Q₀E₁₂ .

Напряжением U на участке 1 — 2 называется физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) исторонних сил при перемещении единичного положительного заряда на данном участке цепи. Таким образом, согласно (97.4),

Понятие напряжения является обобщением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов в том случае, если наэтом участке не действует ЭДС, т.е. сторонние силы отсутствуют.