Вычислить определитель Δ3:3х3 разложением по любому столбцу

Вычислить определитель Δ3 : 3х3 "звездочкой", предварительно упростив.

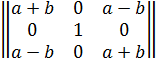
Решение:

Метод «звездочкой».

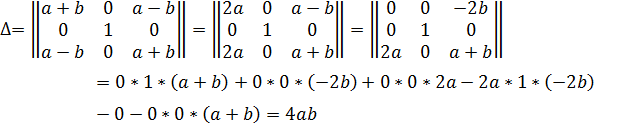
Ответ: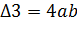

Задание №2.

Вычислить определитель Δ3: 3х3 дописыванием столбцов или строк. Предварительно упростив.

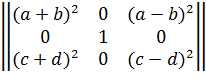
Решение:

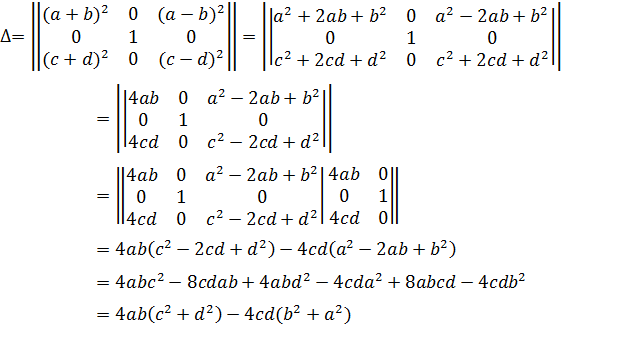
Задание №3.

Вычислить определитель Δ3:3х3 разложением по любому столбцу

Решение:

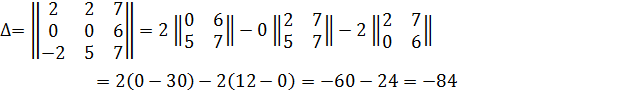
Задание №6.

Решить систему линейных уравнений A*X= F 3x4 методом Крамера. Проверить подстановкой.

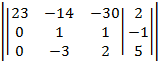
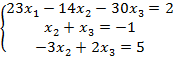
Решение:

1. Найдем главный определитель.

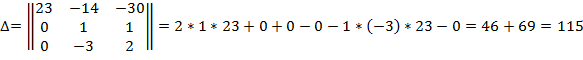
2. Вычислим 1-ый определитель, для нахождения :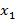

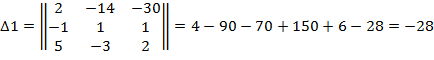
3. Вычислим 2-ой определитель, для нахождения :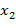

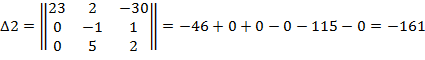
4. Вычислим 3-ий определитель, для нахождения :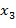

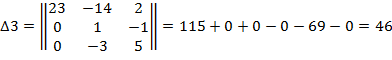
5. Найдем решения системы:

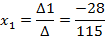
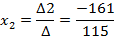
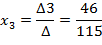
Проверка:

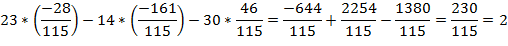
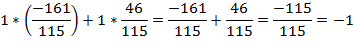
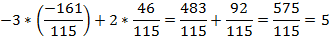
Задание №7.

Решить систему линейных уравнений A*X= F 3x4 методом Гаусса. Проверить подстановкой.

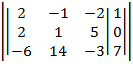
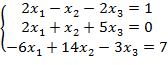
Решение:

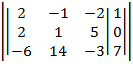
1. В 1-м столбце находим главный (максимальный) элемент: 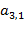= -6

2. Меняем строки 1 и 3 местами.

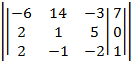
3. Разделили 1-ю строку на главный элемент

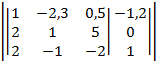
4. Находим коэффициенты, чтобы получить нули в 1-м столбце:

k[2] = -2

k[3] = -2

5. Умножаем строку с главным элементом на коэффициент и прибавляем эту строку к остальным строкам.

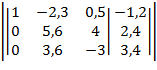
6. В 2-м столбце находим главный (максимальный) элемент: 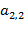= 5,6

Т.к. главный элемент находится в 2-й строке, то строку не изменяем.

7. Разделили 2-ю строку на главный элемент

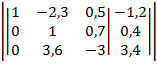
8. Находим коэффициенты, чтобы получить нули в 2-м столбце:

k[3] = -3,6

Умножаем строку с главным элементом на коэффициент и прибавляем эту строку к остальным строкам.

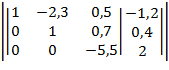
Теперь из полученной расширенной матрицы составляем систему уравнений:

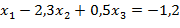
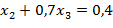
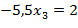
Из системы находим:

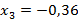
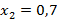
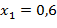
Проверка:

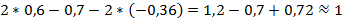
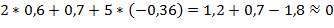
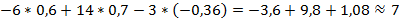
Задание №9.

Найти обратную матрицу М3^обрдля M3:3х3. Проверить умножением М3*М3^обр

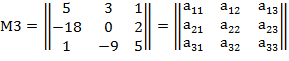
Решение:

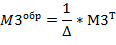
1. Найдем определитель матрицы.

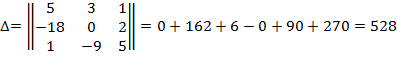
2. Найдем транспонированную матрицу.

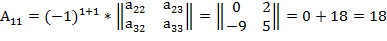
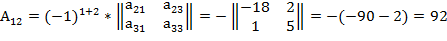
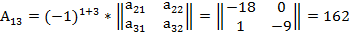
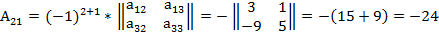
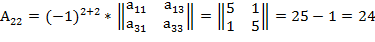
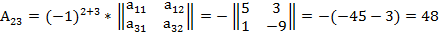
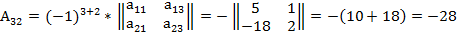
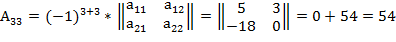
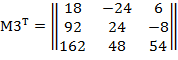
3. Вычислим обратную матрицу.

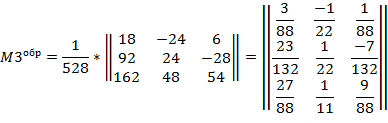
Проверка:

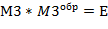
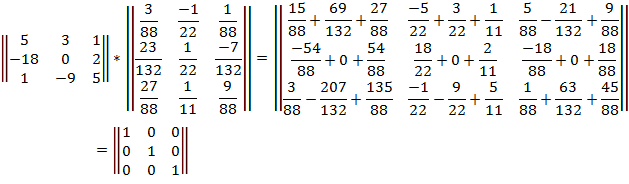
Задание №10.

Найти обратную матрицу М3 ^обр для M3:3х3 методом Гаусса. Проверить умножением М3*М3 ^обр

Решение:

Найдем матрицу М3 ^обр обратную к матрице М3.

Для этого напишем расширенную матрицу , в левой части которой находится наша исходная матрица М3, а в правой единичная. Применяя метод Гаусса, последовательно будем приводить нашу исходную матрицу ( левую часть расширенной матрицы ) к единичной матрице. Причем совершенные преобразование мы будем применять ко всей расширенной матрице. Приведя левую часть расширенной матрицы к единичной, правая часть будет являться обратной матрицей к нашей исходной.

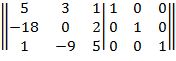
Поменяем местами строки 1 и 3 .

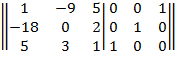
Из элементов строки 2 вычитаем соответствующие элементы строки 1, умноженные на -18

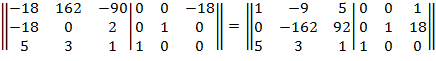
Из элементов строки 3 вычитаем соответствующие элементы строки 1, умноженные на 5 .

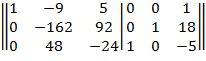
Поменяем местами строки 2 и 3 .

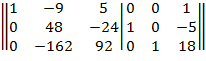
Из элементов строки 1 вычитаем соответствующие элементы строки 2, умноженные на -3/16 .

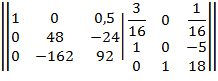
Из элементов строки 3 вычитаем соответствующие элементы строки 2, умноженные на -27/8 .

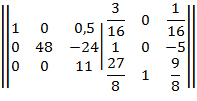
Из элементов строки 1 вычитаем соответствующие элементы строки 3, умноженные на 1/22

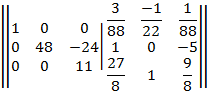
Из элементов строки 2 вычитаем соответствующие элементы строки 3, умноженные на -24/11

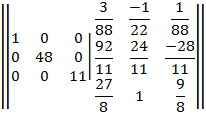
Элементы строки 2 разделим на 48 .

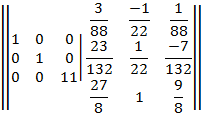
Элементы строки 3 разделим на 11 .

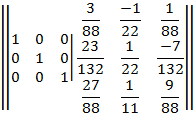
Проверка.

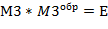
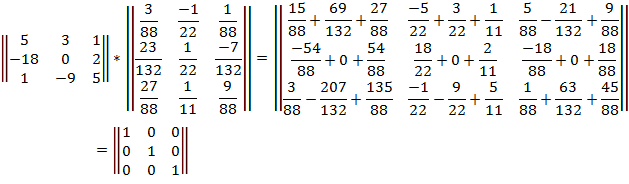
Задание №14