Инерционное (апериодическое) звено
Одним из самых распространенных звеньев систем автоматического управления является инерционное звено. Оно описывается дифференциальным уравнением
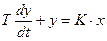 , (3.32)
, (3.32)
Передаточная функция инерционного звена
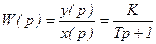 , (3.33)
, (3.33)
Такую передаточную функцию можно получить, если охватить отрицательной обратной связью идеальное интегрирующее звено так, как это показано на рисунке 3.4, а.
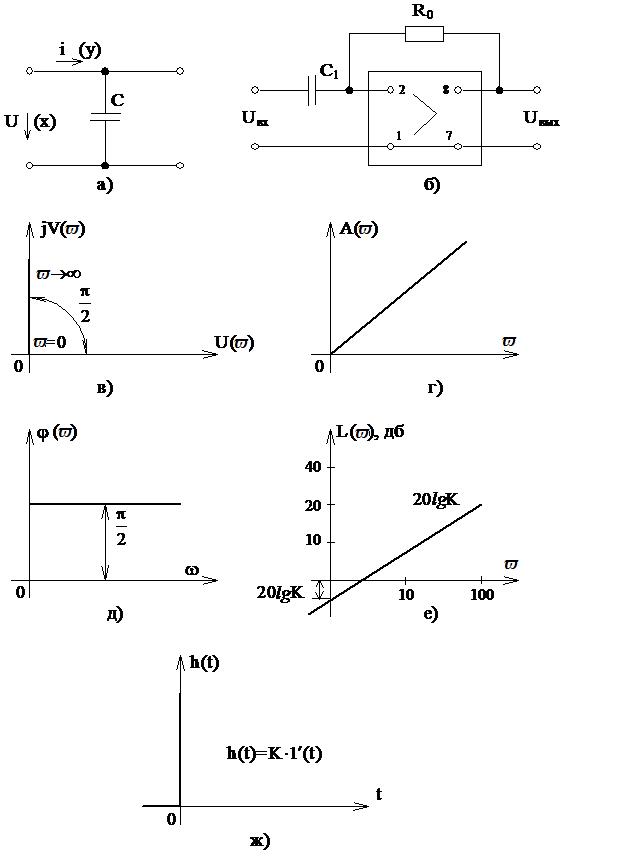
Рисунок 3.3 Характеристики идеального дифференцирующего звена
Ранее мы уже обращались несколько раз к такому звену. В рассматриваемом примере генератор и тиристорный преобразователь являются апериодическими звеньями. Апериодическое звено можно реализовать посредством операционного усилителя, если в обратную связь последнего включить параллельно емкость и сопротивление. В этом случае (рисунок 3.4,б)
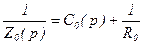 , (3.34)
, (3.34)
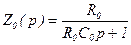 , (3.35)
, (3.35)
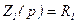 , (3.36)
, (3.36)
Тогда
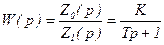 , (3.37)
, (3.37)
где 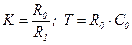 .
.
Апериодическое звено можно реализовать так же включением емкости и сопротивления так, как это показано на рисунке 3.4,в. Передаточная функция полученного звена определятся, как отношение выходного комплексного сопротивления к входному:
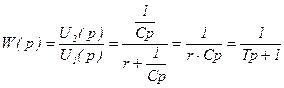 , (3.38)
, (3.38)
Подставляя в (3.33) p=jϖ, получим частотную передаточную функцию
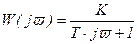 , (3.39)
, (3.39)
Для построения АФХ найдем вещественную и мнимую части, умножив числитель на комплексное выражение, сопряженное знаменателю
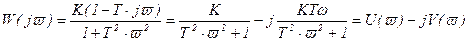 , (3.40)
, (3.40)
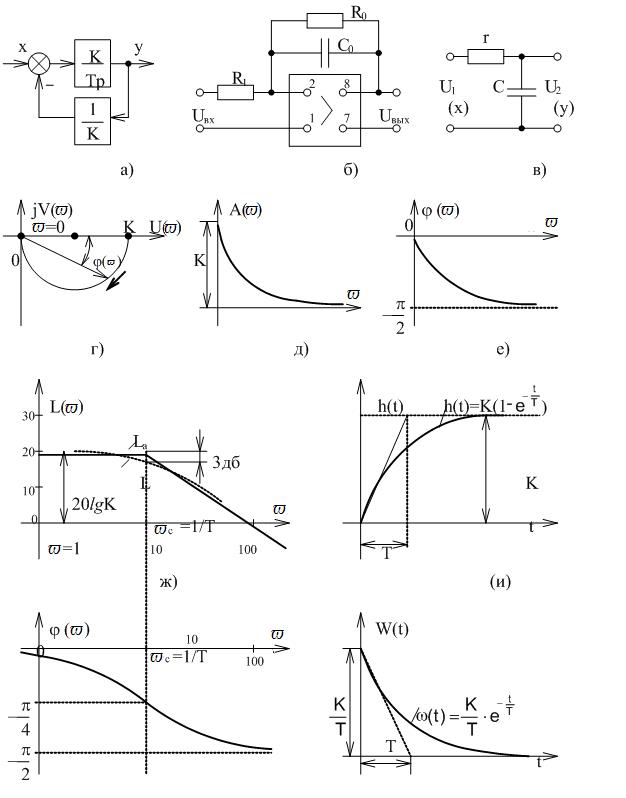
Рисунок 3.4 Характеристики апериодического звена
Нетрудно показать, что АФХ апериодического звена представляет собой полуокружность (рисунок 3.4,г) с центром на вещественной оси, находящимся на расстоянии 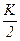 от начала координат. Значению ϖ=0 на АФХ соответствует точка с координатами (K, j0), а ϖ=¥ точка в начале координат.
от начала координат. Значению ϖ=0 на АФХ соответствует точка с координатами (K, j0), а ϖ=¥ точка в начале координат.
Амплитудно-частотная характеристика
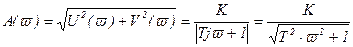 , (3.41)
, (3.41)
Фазовая частотная характеристика
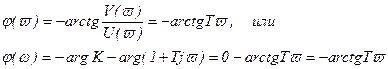 , (3.42)
, (3.42)
АЧХ и ФЧХ апериодического звена показаны на рисунке 3.4,д,е.
Логарифмическая амплитудная частотная характеристика
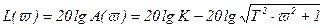 , (3.43)
, (3.43)
показана на рисунке 3.4,ж штриховой линией L.
Построение ЛАХ можно значительно упростить, найдя ее асимптоты.
Если 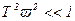 , то
, то 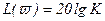 , (3.44)
, (3.44)
Если 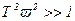 , то
, то 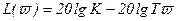 , (3.45)
, (3.45)
Выражение (3.45) представляет собой уравнение прямой линии. Определим угол наклона этой прямой к оси абсцисс, для чего найдем ординату при изменении частоты в 10 раз, то есть ϖ 1=10ϖ. Тогда
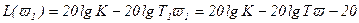 , (3.46)
, (3.46)
Выражение (3.44) показывает, что изменение ϖ в 10 раз соответствует уменьшению ординаты ЛАХ на -20 дб. Найдем частоту, при которой происходит пересечение горизонтальной и наклонной асимптот. Эта частота называется частотой сопряжения ϖс и определяется из совместного решения уравнений асимптот.
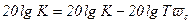 , (3.47)
, (3.47)
откуда
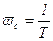 , (3.48)
, (3.48)
Учитывая (3.44), (3.45) и (3.48), составим уравнение для асимптотической ЛАХ.
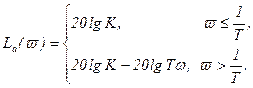 , (3.49)
, (3.49)
График характеристики La(ϖ) представлен на рис.3.1.3.1,ж сплошной линией.
Наибольшая разница ординат асимптотической и точной ЛАХ имеет место при ϖ=ϖ с и равна примерно 3 дб, что во многих практических расчетах оказывается допустимым, чтобы ограничиться построением асимптотической ЛАХ.
ЛФХ апериодического звена представлена на рисунке 3.4,з. Следует отметить, что особенностью ЛФХ является ее асимметрия относительно частоты сопряжения ϖс и сдвиг фазы на этой частоте j=-45°.
Для переходной функции, используя таблицу соответствий изображений и оригиналов, получим
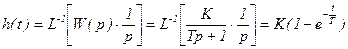 , (3.50)
, (3.50)
Весовая функция
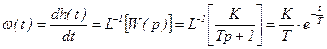 , (3.51)
, (3.51)
Временные характеристики апериодического звена показаны на рисунке 3.4, и,к.
