Инерционное звено 2-го порядка
Такие звенья описываются дифференциальным уравнением вида
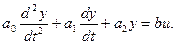
Преобразуем по Лапласу это уравнение:
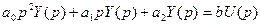 или
или 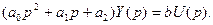
Определим передаточную функцию звена
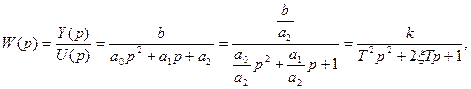
где 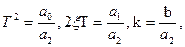
T – постоянная времени, с;
x – коэффициент затухания (безразмерная величина);
k – передаточный коэффициент.
В зависимости от величины x классифицируются звенья второго порядка по видам:
(1) (2) (3) (4) (5)



 x
x
-1 0 1
1-неустойчивое апериодическое звено;
2-неустойчивое колебательное звено;
3-консервативное звено;
4-колебательное звено;
5-апериодическое звено II порядка.
1. x>1 – апериодическое звено II-го порядка.
Характеристическое уравнение звена 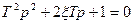 имеет корни действительные и отрицательные
имеет корни действительные и отрицательные 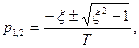 данное звено можно представить в виде двух последовательно соединенных звеньев с различными постоянными времени:
данное звено можно представить в виде двух последовательно соединенных звеньев с различными постоянными времени:
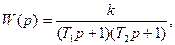 тогда при T1>T2 переходная функция звена имеет вид
тогда при T1>T2 переходная функция звена имеет вид
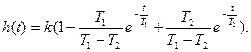
Переходная характеристика:
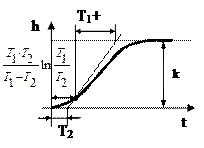 |
2. x=1, 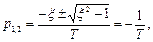 оба корня одинаковые и отрицательные.
оба корня одинаковые и отрицательные.
Передаточная функция преобразуема к двум последовательно соединенным апериодическим звеньям с одинаковыми постоянными времени.
W(p)= 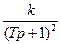 ,переходная функция h(t)=1-(1+at)e-at ,где a=1/T.
,переходная функция h(t)=1-(1+at)e-at ,где a=1/T.
3. 0<x<1, 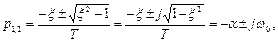 корни разные, комплексно-сопряженные, с отрицательной вещественной частью; КОЛЕБАТЕЛЬНОЕ ЗВЕНО.
корни разные, комплексно-сопряженные, с отрицательной вещественной частью; КОЛЕБАТЕЛЬНОЕ ЗВЕНО.
Переходная функция звена имеет вид
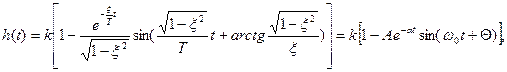
где 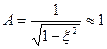 при малых x,
при малых x, 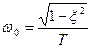 - имеет физический смысл собственной частоты колебаний,
- имеет физический смысл собственной частоты колебаний, 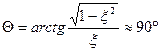 при малых x.
при малых x.
Период собственных колебаний 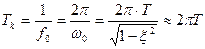 при малых x.
при малых x.
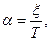
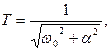
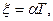
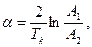
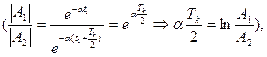
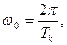
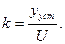
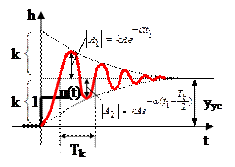
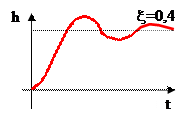
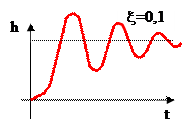 Чем меньше x, тем выше колебательность процесса:
Чем меньше x, тем выше колебательность процесса:
 |
4. x=0, 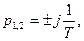 такое звено имеет специальное название – КОНСЕРВАТИВНОЕ ЗВЕНО.
такое звено имеет специальное название – КОНСЕРВАТИВНОЕ ЗВЕНО.
Передаточная функция звена: 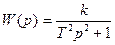 .
.
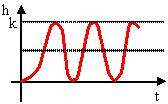
Решение дифференциального уравнения имеет вид
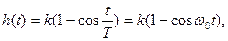 где
где 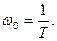
5. 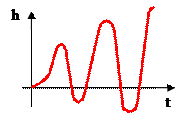 -1<x<0,
-1<x<0, 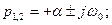
Это неустойчивое колебательное звено.
6. x<-1.

7. x=-1; отличается от случая 6 лишь тем, что корни одинаковые.
Критерий Найквиста, сформулированный Я.З.Цыпкиным. Формулировка критерия Найквиста для ЛЧХ.
Критерий устойчивости Найквиста
Формулировка Я.З. Цыпкина
| Замкнутая система устойчива, если при изменении w от нуля в сторону положительных значений до ¥ разность числа положительных и отрицательных переходов АФХ разомкнутой системы через полупрямую (-¥, -1) равна m/2. |
Критерий Найквиста для ЛЧХ
| Для того чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы при всех значениях w, где L(w)>0, разность числа положительных и отрицательных переходов фазовой характеристики разомкнутой системы через линии ±(2k+1)p (k=0,1,2,…) равнялась m/2, где m - число полюсов с положительной вещественной частью в передаточной функции разомкнутой цепи системы. |
Примечание: фазовая характеристика ЛЧХ астатических систем дополняется монотонным участком +np/2 при w®0.
Принцип аргумента
В основе частотных методов лежит принцип аргумента.
Проведем анализ свойств многочлена вида:
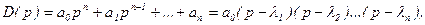 где li - корни уравнения
где li - корни уравнения
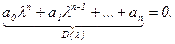
На комплексной плоскости каждому корню соответствует вполне определенная точка. Геометрически каждый корень li можно изобразить в виде вектора, проведенного из начала координат в точку li: |li| - длина вектора, argli - угол между вектором и положительным направлением оси абсцисс. Отобразим D(p) в пространство Фурье, тогда 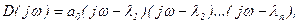 где jw-li - элементарный вектор.
где jw-li - элементарный вектор.
Концы элементарных векторов находятся на мнимой оси.
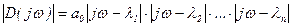 - модуль вектора, а аргумент (фаза)
- модуль вектора, а аргумент (фаза) 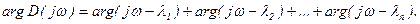
Направление вращения вектора против часовой стрелки принимают за ПОЛОЖИТЕЛЬНОЕ. Тогда при изменении w от 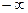 до
до 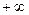 каждый элементарный вектор (jw-li) повернется на угол +p, если li лежит в левой полуплоскости.
каждый элементарный вектор (jw-li) повернется на угол +p, если li лежит в левой полуплоскости.
Пусть D(l)=0 имеет m корней в правой полуплоскости и n-m корней в левой, тогда при возрастании w от 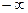 до
до 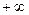 изменение аргумента вектора D(jw) (угол поворота D(jw), равный сумме изменений аргументов элементарных векторов) будет
изменение аргумента вектора D(jw) (угол поворота D(jw), равный сумме изменений аргументов элементарных векторов) будет 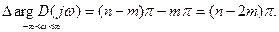

   Изменение аргумента вектора D(jw) при возрастании w от Изменение аргумента вектора D(jw) при возрастании w от 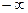 до до 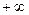 равно разности (n-m) корней уравнения D(l)=0, лежащих в левой части плоскости, и числом m корней уравнения, лежащих в правой части плоскости, умноженной на p. равно разности (n-m) корней уравнения D(l)=0, лежащих в левой части плоскости, и числом m корней уравнения, лежащих в правой части плоскости, умноженной на p. |
Принцип аргумента:
Экзаменационный билет №14
1. Логарифмические частотные характеристики колебательного звена
Частотная передаточная функция колебательного звена имеет вид
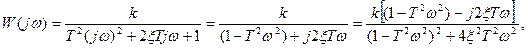 откуда
откуда 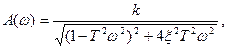
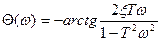 , при
, при 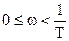
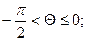
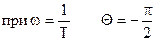 ; при
; при 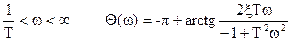 .
.
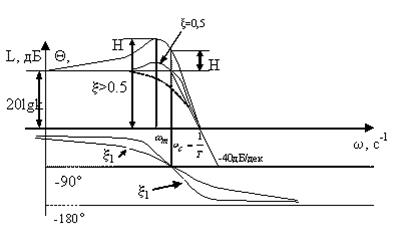
Логарифмическая амплитудно-частотная функция имеет вид
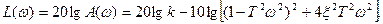
1. 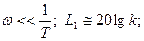 низкочастотная асимптота имеет наклон 0 дБ/дек;
низкочастотная асимптота имеет наклон 0 дБ/дек;
2. 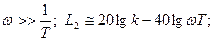 высокочастотная асимптота имеет наклон – 40дБ/дек.
высокочастотная асимптота имеет наклон – 40дБ/дек.
3. 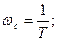 обе асимптоты пересекаются на сопрягающей частоте.
обе асимптоты пересекаются на сопрягающей частоте.
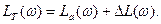
щщ
При значениях 0,5 < x<1 характеристика близка к ломаной. Если же x<0,5, то получается заметный выступ в окрестности ωс. Здесь необходимо вычислять превышение 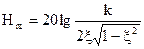 на частоте
на частоте 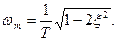 В упрощенных расчетах достаточно находить
В упрощенных расчетах достаточно находить 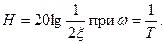
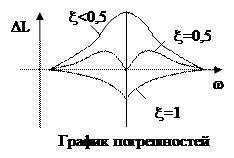
Величина погрешности на сопрягающей частоте для различных x: 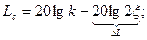
при x=1 DL= -6,
x=0,5 DL=0,
x=0,1 DL=14.
Если x от 1 до 0,3, то можно не строить точную ЛАЧХ, а довериться асимптотической.
Примеры колебательных звеньев: двигатели постоянного тока, LRC-цепи, регуляторы Уатта и др.
2. Критерий Найквиста: причины широкого применения в инженерной практике, критерий Найквиста для систем, устойчивых в разомкнутом состоянии.
Критерий Найквиста базируется на частотных характеристиках разомкнутой цепи САУ, так как по виду частотных характеристик разомкнутой цепи можно судить об устойчивости замкнутой системы.
Критерий Найквиста нашел широкое применение в инженерной практике по следующим причинам:
1. Устойчивость системы в замкнутом состоянии исследуют по частотной передаточной функции ее разомкнутой цепи, а эта функция, чаще всего состоит из простых сомножителей. Коэффициентами являются реальные параметры системы, что позволяет выбирать их из условий устойчивости.
2. Для исследования устойчивости можно использовать экспериментально полученные частотные характеристики наиболее сложных элементов системы (объект регулирования, исполнительный орган), что повышает точность полученных результатов.
3. Исследовать устойчивость можно по ЛЧХ, построение которых несложно.
4. Удобно определять запасы устойчивости.
