Методы получения математических моделей

Математическая модель

Математическая модель — это математическое представление реальности, представляющее собой частный случай понятия модели, как системы, исследование которой позволяет получать информацию о некоторой другой системе.

Процесс построения и изучения математических моделей называется математическим моделированием.

Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют объект его математической моделью и затем изучают последнюю. Связь математической модели с реальностью осуществляется с помощью цепочки гипотез, идеализаций и упрощений.

Математическую модель объекта удобно представить в виде блок-схемы, т.е. параметрической схемы, в которой прямоугольник соответствует объекту или системе, стрелки X, Х(t) означают вход­ные параметры (факторы) или воздействия на систему, а стрелки У, У(t) — выходные параметры. На схеме внутри прямоугольника вписывают оператор или динамическую характеристику.

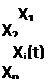A{ }

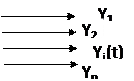Рис. 1 Блок-схема математической модели

Зная математическую модель процесса или объекта, можно спрогнозировать свойства выходящего продукта, оценить степень влияния входных факторов с целью разработки схемы контроля и стабилизации наиболее сильно влияющих факторов, а также осу­ществить оптимизацию процесса.

Математическая модель считается адекватной объекту, если с достаточной точностью отражает ее поведение, т.е. изменения вы­ходных параметров при варьировании (изменении) входных пара­метров (факторов) в заранее заданном диапазоне.

В основу классификации математических моделей положены следующие признаки:

1. Число и характеристика аргументов :

а) если входные параметры процесса или оператор не зависят от аргументов, то математическая модель называется статической. Этот вид модели обычно описывается алгебраическим уравнением:

Y = f(X₁,…, X_n)

б) если входные параметры процесса или оператор зависят от аргументов, то такая модель называется динамической. Если пара­метр процесса или оператор зависит только от одного аргумента, например, от времени Х==Х(t), модель называется динамической мо­делью с сосредоточенными параметрами, т.е.

Y(t) = A(t){X(t)}

Эти модели описываются обыкновенными дифференциальны­ми уравнениями;

в) если число независимых аргументов более одного (например, время и пространственные координаты), то такая модель называется математической моделью с распределенными параметрами, т.е.

У(t,x,y,z)=А(t,x,y,z){Х(t,x,y,z)}.

Эти модели описываются дифференциальными уравнениями в частных производных.

2. Природа исследуемого процесса или объекта. По этому признаку модели делятся на вероятностные и детерминированные.

В вероятностной модели учитывается случайная природа входных параметров или оператора. Вероятностные модели могут быть нескольких видов:

а) если выходной параметр процесса представляет случайную величину, а факторы (входные параметры) являются не случайными, то математическая модель называется регрессионной (регрессия — движение назад). Случайные значения выходного параметра могут быть обусловлены, например, воздействием части неучтенных факто­ров. Эта модель позволяет предполагать, что причина изменения вы­ходного параметра содержит в себе две части: одна неслучайная, яв­ляется функцией факторов; другая случайная, не связана с факторами.

При построении регрессионных моделей используются раз­личные виды алгебраических уравнений;

б) если выходной параметр процесса и факторы представляют случайные величины с определенным законом распределения, то взаимосвязь между ними или математическая модель процесса назы­вается корреляционной (корреляция — соотношение). В этом случае к вопросам выяснения зависимости между случайными величинами параметров процесса еще добавляются вопросы исследования степе­ни связи между ними, и при построении этих моделей используется корреляционный анализ случайных величин;

в) в детерминированной модели не учитывается случайная природа входных параметров процесса или оператора, а выходные параметры процесса однозначно определяются факторами и опера­тором процесса. В этом случае не требуются математико-статистические методы анализа процесса.

3. Свойство линейности модели. Математическая модель на­зывается линейной, если линеен оператор системы. Оператор А{ } называется линейным, если выполняется равенство

A{X+DX}=A{X}+A{DX}

где DХ — символ произвольного приращения входных параметров.

Это свойство линейного оператора называется также свой­ством суперпозиции, или наложения. Если это равенство не выпол­няется, то оператор и соответственно модель называется нелинейной.

Методы получения математических моделей

Методы получения математических моделей подразделяются на теоретические и экспериментальные.

Теоретический метод заключается в аналитическом исследова­нии физической сущности процесса с использованием общих законов физики, или процессов с использованием уравнений материального и энергетического баланса.

Применение чисто теоретического метода представляет боль­шую трудность вследствие сложности явлений, происходящих в про­цессах, или недостаточной степени изученности их.

Экспериментальный метод математического описания заклю­чается в обработке экспериментальных данных, полученных непо­средственно на действующих объектах производства, или на полу­промышленной лабораторной машине, или физической модели про­цесса — стенде.

Наиболее эффективным методом получения математической модели является сочетание теоретического и экспериментальных ме­тодов. При этом на долю теоретического метода приходится анализ в основном структурных свойств объекта и продуктов и получение общего вида уравнений, а на долю экспериментального — количе­ственный анализ и проверка теоретических выводов.