Определение отношения теплоемкостей газа методом адиабатического расширения

Цель работы: определить отношение теплоемкостей газа методом адиабатического расширения.

Приборы и принадлежности: закрытый стеклянный баллон, 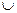- образный водяной манометр, насос.

Теоретические сведения

Состояния газа определяются тремя величинами - параметрами состояния: давлением Р, объемом V и термодинамической температурой Т. Уравнение, связывающее эти параметры, называется уравнением состояния газа. Для идеального газа уравнением состояния является уравнение Менделеева-Клапейрона, которое для одного моля имеет вид

PV₀=RT, (9.1)

где R -универсальная газовая постоянная; V₀ - объем одного моля газа.

Идеальный газ - газ, взаимодействие между молекулами которого равно нулю, столкновения абсолютно упругие, объем молекул бесконечно мал по сравнению с объемом, занимаемым газом.

Реальные газы при нормальных условиях могут быть с достаточной степенью точности описаны с помощью уравнений для идеального газа.

Удельной теплоемкостью вещества С_уд называется физическая величина, численно равная количеству тепла, которое надо сообщить единице массы этого вещества, чтобы увеличить его температуру на 1°С.

Для газов удобно пользоваться молярной теплоемкостью С, кото­рая характеризуется количеством тепла, необходимым для нагревания одного моля вещества на 1°С.

Очевидно,

,

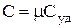где μ - молярная масса данного вещества; С_уд - удельная теплоемкость. Величина теплоемкости газов зависит от условий нагревания. Выясним эту зависимость с помощью уравнения состояния идеального газа (9.1) и первого начала термодинамики, которое формулируется следующим образом: dQ -количество теплоты, переданное системе (газу), затрачивается на увеличение ее внутренней энергии (нагревание) dU и на работу dA, совершаемую системой (газом) при расширении, т.е.

dQ=dU+dA (9.2)

Работа газа против внешних сил при его расширении dA=PdV где dV - изменение объема газа.

Предварительно рассмотрим основные процессы, которые могут происходить в идеальном газе, когда количество вещества газа остается постоянным и равным 1 молю.

Изохорический процесс - процесс, при котором нагревание газа происходит без изменения его объема, т.е. V=const. Работы газ не совершает, следовательно, согласно первому началу термодинамики (9.2), все тепло, подводимое к газу, идет на увеличение его внутренней энергии. Тогда молярная теплоемкость газа при постоянном объеме, ис­ходя из уравнения (9.2),

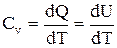(9.3)

Изобарический процесс - процесс, протекающий при постоянном давлении, т.е. P=const. При нагревании газа при постоянном давлении его объем возрастает, сообщаемое газу тепло идет не только на увеличение его внутренней энергии dU, но и на совершение работы против внешних сил dA. Тогда молярная теплоемкость газа при постоянном давлении:

,

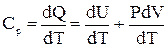т.е. C_p=C_v+R, (9.4)

где 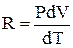-универсальная газовая постоянная.

Физический смысл универсальной газовой постоянной состоит в том, что она численно равна работе, которую совершает 1 моль газа в результате его расширения при постоянном давлении с повышением температуры на 1°С. Выражение (9.4) носит название уравнения Майера.

Изотермический процесс - процесс, протекающий при постоянной температуре, т.е. T=const В этом случае внутренняя энергия газа не изменяется (dU=0), и все подводимое к газу тепло идет на совершение работы, т.е.

dQ=dA=PdV . (9.5)

Адиабатический процесс - процесс, протекающий без теплообме­на с окружающей средой, т.е. dQ=0. Тогда

dA=-dU. (9.6)

Отсюда следует, что в адиабатическом процессе работа может производиться лишь за счет изменения внутренней энергии системы.

Для протекания адиабатического процесса система должна быть окружена абсолютно нетеплопроводящими стенками. Но так как этого до­стичь нельзя, то всякий реальный процесс может происходить лишь как более или менее точное приближение к адиабатическому. Практически близкими к адиабатическому оказываются процессы, протекающие на­столько быстро, что теплообмен с внешней средой не успевает произой­ти.

Адиабатические процессы описываются уравнением Пуассона:

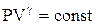,(9.7)

где 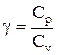- показатель адиабаты.

Непосредственное экспериментальное определение теплоемкостей газа С_р и C_v затруднительно, т.к. они составят ничтожную долю теплоемкостей сосуда, заключающего газ, и поэтому измерение будет неточным. Обычно измеряют γ=C_p/C_v, которое входит в уравнение Пуассона. Поэтому в настоящей работе для определения γ предлагается метод адиабатического расширения газа.

Описание установки

Используемая установка (рис. 9.1) состоит из стеклянного баллона А, соединенного с манометром М и насосом. Если при помощи насоса накачать в баллон некоторое количество воздуха, то его давление и температура повысятся. Вследствие теплообмена с окружающей средой температура воздуха в баллоне через некоторое время сравняется с температурой окружающей среды. Давление Р, установившееся в баллоне, больше атмосферного на величину давления столба h₁ определяемую разностью уровней жидкостей в коленах манометра (рис. 9.1).

Если обозначить через m массу воздуха в баллоне при атмосферном давлении, то при давлении Р₁ воздух займет меньший объем, чем объем сосуда. Обозначим этот объем через V₁; тогда состояние воздуха массой m внутри баллона будет характеризоваться параметрами Р_{1 ,} V_{1 ,} Т₁ = Т_комн

На рис. 9.2 данному состоянию соответствует точка M₁. Если открыть на короткое время кран В, то воздух в баллоне расширится. Давление внутри баллона в конце расширения равно атмосферному Р₀, объем рассматриваемой массы воздуха равен объему сосуда V.

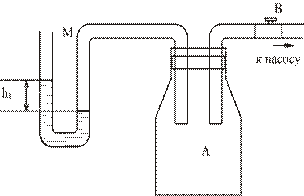
Рис. 9.1

Так как процесс быстрого расширения воздуха можно считать адиабатическим, то температура Т₂ станет ниже комнатной. Следовательно, в конце адиабатического расширения (точка М₂ на рис. 9.2) параметры будут Р₀, V₂, Т₂.

Применяя к этим состояниям уравнение Пуассона, получим

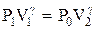(9.8)

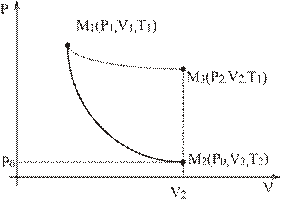
Рис. 9.2

Закроем кран В. Охладившийся при расширении воздух в баллоне через некоторое время вследствие теплообмена нагреется до комнатной температуры (процесс нагревания является изохорическим). Это приведет к возрастанию давления воздуха до некоторой величины Р₂. Поэтому давление будет больше атмосферного на величину давлениястолба h₂, определяемую разностью уровней жидкости в коленах мано­метра. Параметры этого состояния (точка М₃) - Р₂, V₂ Т₁=Т_комн

Начальное и конечное состояния газа наблюдаются при одинако­вой температуре, поэтому на основании закона Бойля-Мариотта можно записать:

P₁V₁=P₂V₂ . (9.9)

На графике (рис. 9.2) показаны процессы перехода газа из одного состояния в другое. Линия М₁М₂ - адиабата, М₂М₃ - изохора, М₁М₃ -изотерма.

Найдем значение γ. Для этого обе части уравнения (9.9) возведем в степень γ:

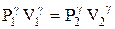. (9.10)

Затем разделим уравнение (9.10) на уравнение (9.8) и полученное выраже­ние прологарифмируем.

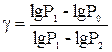(9.11)

Учитывая, что давления P₀,P_1,P₂ отличаются друг от друга не­значительно, в формуле (9.11) разности логарифмов можно заменить разностями самих чисел:

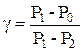(9.12)

Зная, что Р₀ - атмосферное давление, а давления Р₁ и Р₂ превы­шают атмосферное соответственно на величину давления столбов жид­кости в манометре высотой h₁ и h₂, т.е.

P₁ = P₀+ρgh₁; P₂ = P₀+ρgh₂,

где р - плотность жидкости; g - ускорение свободного падения,

получим: 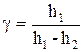(9.13)

Формула (9.13) является расчетной для определения γ. Разности уровней жидкости h₁ и h₂ измеряются непосредственно из опыта.

Порядок выполнения работы

1.Ознакомиться c устройством зажима.

2. Осторожно накачать в баллон воздух так, чтобы разность уровней
жидкостей в коленах манометра составляла 15-20 см. Пережать шланг зажимом и отсоединить насос. Выждать (1-2мин), когда положение
уровней жидкости в манометре перестанет изменяться. (При накачива­нии воздух, сжимаемый под поршнем насоса, нагревается. Вследствие
теплообмена с окружающей средой с течением времени происходит понижение температуры воздуха в баллоне и вместе с этим понижение уровней жидкости). Измерить h₁ - разность высот жидкости в коленах манометра.

3. Открыть зажим; как только уровни жидкости в манометре сравняют­ся, закрыть его. Тогда охлажденный при адиабатическом расширении воздух в баллоне будет нагреваться до комнатной температуры, что приведет к изменению уровней жидкости в манометре. Выждав 1-2мин, когда положение уровней жидкости в манометре перестанет изменять­ся, измерить h₂ - разность высот жидкости в коленах манометра. Результаты измерений записать в таблицу. Опыт повторить 5 раз.

Таблица

h1	h2	γ	Δγ=|γср-γ|
		γср	Δ γср

4. По формуле (9.13) вычислить γ для каждого опыта.

5. Найти для каждого опыта Δγ по формуле Δγ=|γ_ср-γ_i|, где γ_i значение
для каждого опыта.

6. Определить Δγ_ср как среднее арифметическое значение Δγ_i , взятых
по абсолютному значению.

7. Результат записать в виде γ= γ_ср ± Δγ_ср

Контрольные вопросы

1.Что такое моль? Как связаны моль и число Авогадро?

2. Какой газ называют идеальным? При каких условиях для реальных
газов можно применять формулы, полученные для идеального газа?

3. Что называют степенью свободы? Как подсчитать их число?

4. Чем отличаются удельная и молярная теплоемкости? Укажите их
размерности и связь друг с другом.

5. Почему теплоемкость газа зависит от условий нагревания? Какая из теплоемкостей C_v и С_р больше и почему?

6. Как будет выглядеть уравнение Майера для удельных теплоемкостей?

7 . Объяснить физический смысл постоянной R в уравнении Майера и указать ее размерность.

8 . Написать уравнение состояния идеального газа. Получить из него уравнения
изопроцессов.

9. Применить первое начало термодинамики для изопроцессов.

10. Какой процесс называют адиабатическим? При каких условиях реальные про­цессы можно считать адиабатическими? Выполняются ли эти условия в данной работе?

ЛАБОРАТОРНАЯ РАБОТА №10