Относительная ошибка аппроксимации

Оценивает отклонение теоретических оценок от реальных. Ошибка аппроксимации ε. Формула 17.

Значение этой ошибки, не превышающее 8-10% говорит о хорошем качестве уравнения регрессии.

Εср=2,6²/30*100%=8,7%.

В регрессионном анализе общая колеблемость результата представляется следующим образом:

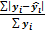∑= *100%

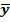∑(y- 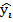)²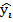=∑(y_i- )²+∑( -y_i)²

∑(y- 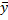)²-общая колеблемость результата, ∑(y- 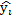)²–от фактических данных отнимаем теоретические = остаточная колеблемость, ∑( 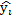-y_i)² –колеблемость результата, объясненная уравнением регрессии

Это разложение вариации зависимой переменной лежит в основе качества полученного уравнения регрессии, т.е. чем бОльшая часть вариации у объясняется уравнением регрессии, тем лучше качество уравнения, т.е. правильно выбран тип функции для описания зависимости результата и фактора y=f(x) и правильно выбрана сама объясняющая переменная х. отношение объясненной вариации к общей позволяет найти индекс детерминации η².

η²=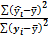

Он определяет степень детерминации регрессией вариации у. Корень квадратный из индекса детерминации называется теоретическим корреляционным отношением, оно показывает тесноту связи между результатом и фактором, как при линейной, так и при нелинейной связи. Измеряется η[0,1].

В нашем примере∑( 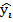- 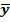)²=∑(y_i- 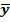))²+∑( 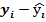)² = 7,5-1,094=6,064,

η²=6,406/7,5=0,85 (85%)

Оценка значимости производится на основе F-критерия Фишера, которому предшествует дисперсионный анализ, применяемый как вспомогательное средство для изучения качества регрессионной модели. Схему дисперсионного анализа представим в таблице, где n-число наблюдений, а m-число параметров при х.

Таблица дисперсионного анализа

Компоненты дисперсии	Сумма квадратов (SS)	Число степеней свободы (df)	Дисперсия на одну степень свободы (MS)
Общая дисперсия		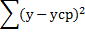n-1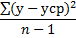
Факторная		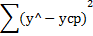m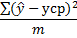
Остаточная		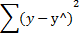n-m-1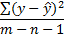

Дисперсия на одну степень свободы приводит дисперсии к сопоставимому виду. Поэтому, сопоставляя факторную и остаточную дисперсии, получают фактическое значение F-критерия Фишера.

F=MS_ФАКТ/MS_ОСТ

Фактическое значение F-критерия Фишера сравнивается с табличным значением F-критерия Фишера F_табл(α,k₁,k₂), которое зависит от уровня значимости α и степеней свободы k₁ (факторная), k₂(остаточная).

Если фактическое значение F-критерия Фишера больше табличного, то уравнение регрессии является статистически значимым в целом

Для парной линейной регрессии этот пример может быть записан следующим образом:

F_факт= 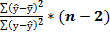, F_факт=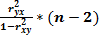

F-критерий Фишера говорит о статистической значимости уравнения. В парной линейной регрессии оценивается значимость отдельных параметров уравнения регрессии aи b. С этой целью определяется его стандартная ошибка:

m_b=MS_ост/σ_x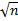

t-критерий Стьюдента. Для оценки существенности коэф-та регрессии определяется фактическое значение t-критерия Стьюдента: фактическое значение t-критерия Стьюдента для параметра b:

t_b=b/m_b

Далее это фактическое значение сравнивается с табличным значением t-критерия Стьюдента, которое зависит от уровня значимости α и числа степеней свободы df (n-2).

Если фактическое значение больше табличного, то параметр регрессии статистически значим. Кроме того, можно определить границы доверительного интервала коэф-та регрессии b.

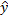=a+bx

b±∆(предельная ошибка)

b-∆­_b≤b≤b+∆_b

∆_b=t_табл*m*b, где∆_b–предельная ошибка коэф-та регрессии b.

Если -2≤b≤3, значит, b-статистически незначим.

Стандартной ошибкой для параметра аm_a = MS_ост .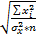

Значимость параметра а определяется аналогично параметру b.

t_a=a/∆_ma

t_a=a/m_a>t_a(α, df)

Если фактическое больше табличного – параметр статистически значим.

Аналогичным образом проверяется статистическая значимость линейногокоэф-та кореляции.

m_σyx=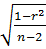

И это значение сравнивается с табличным значением t-критерия Стьюдента.

При прогнозировании по уравнению регрессии вычисляется прогнозное значение результата ( 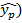подстановкой в уравнение регрессии прогнозного или желаемого значения фактора.

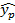=a+bx_np

Полученное по этому уравнению значение результат называется точечным прогнозом.

Здесь также считаются доверительные интервалы прогноза. Они считаются следующим образом:

y_p-∆_y≤ 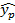≤y_p+∆_p, где ∆_p– предельная ошибка прогноза.

∆y=t_табл*m_y, где m_y- стандартная ошибка прогноза

m_Уp=MS_ост * 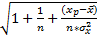, где 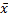- фактическое значение исходных данных.

Выполнить корреляционно-регрессионный анализ можно, воспользовавшись пакетами прикладных программ. Самый простой – Excel.

Нужно в закладке «Данные» - «Анализ данных» - «Регрессия» - «Входной интервал у»

х	у

Поставить флажок «Метки», «Const 0» – флажка не должно быть, иначе параметр а = 0. Дальше «Выходной интервал» номер свободной ячейки на рабочем листе – Ок.

Вывод итогов представляет собой 3 таблички:

1. Регрессионная статистика

МножественныйR (парный линейный коэф-т корреляции)
R-квадрат (коэф-т детерминации)
НормированныйR-квадрат (скорректированный коэф-т корреляции)
Стандартная ошибка коэф-та корреляции
Наблюдение

2. Дисперсионный анализ

	df	SS	MS	F	F значимое
Регрессия (факторная)
Остаток
Итого:

3.

	Коэф-ты	Стандартная ошибка параметров	t-статистика (факт. значения t-критерия для параметров а и b)	Нижняя 95%	Верхняя 95% (границы доверительного интервала)
У - пересечение	Параметр а	Число
х	b	Число

95% -означает, что уровень значимости α = 5% (вероятность – 95%).