Построение линейной однофакторной регрессионной модели зависимости результативного признака Y от фактора Х.

Линейное однофакторное уравнение регрессии имеет вид:

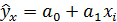
Коэффициенты уравнения регрессии вычисляются по формулам:

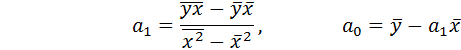
Для расчета коэффициентов строится вспомогательная табл.2.2

(расчеты проведены с применением пакета MS Excel):

Таблица 2.2

Расчетная таблица для построения и анализа

Линейной модели парной регрессии

№п/п		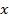		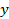	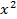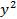xy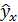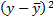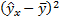
						2175,181	357,21	94,459
						2177,631	357,21	52,838
						2177,631	320,41	52,838
						2180,081	62,41	23,222
						2180,081	24,01	23,222
						2180,081	166,41	23,222
						2180,081	98,01	23,222
						2180,081	118,81	23,222
						2182,531	8,41	5,612
						2182,531	4,41	5,612
						2182,531	50,41	5,612
						2182,531	8,41	5,612
						2182,531	0,01	5,612
						2182,531	9,61	5,612
						2182,531	16,81	5,612
						2182,531	4,41	5,612
						2182,531	26,01	5,612
						2182,531	8,41	5,612
						2184,981	4,41	0,006
						2184,981	292,41	0,006
						2184,981	4,41	0,006
						2184,981	4,41	0,006
						2187,431	26,01	6,406
						2189,881	65,61	24,81
						2189,881	50,41	24,81
						2189,881	50,41	24,81
						2194,781	50,41	97,634
						2197,231	146,41	152,053
						2197,231	50,41	152,053
						2204,581	102,01	387,342
Всего						65546,98	2488,7	1242,317
Среднее	2321,67	2184,9		4773870,967	5072782,467	-	82,956	41,41

Расчет коэффициентов уравнения регрессии на основе данных табл.2.2:

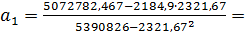0,245

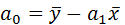= 2184,9-0,245∙2321,67=1616,091

Вывод. Линейная регрессионная модель связи изучаемых признаков имеет вид уравнения

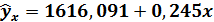
Коэффициент регрессии 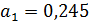показывает, что при увеличении факторного признака Выручка от продажи продукциина 1 млн руб. значение результативного признака Прибыль от продажи продукции увеличивается в среднем на 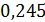млн руб.

3. Проверка уравнения регрессии на адекватность[2].

1. Оценка практической пригодности построенной модели связи

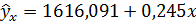по величине коэффициента детерминации R^2.

Расчет R²:

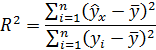
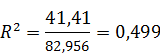
Вывод. Критерий практической пригодности модели связи R² > 0,5 не выполняется. Однако поскольку значение R² практически совпадает с 0,5, можно считать, что построенное регрессионное уравнение в достаточной мере отражает фактическую зависимость признаков и пригодно для практического применения.

2. Оценка статистической значимости (неслучайности) коэффициента R²по F-критерию Р.Фишера рассчитывается по формуле:

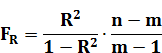
где m – число коэффициентов уравнения регрессии (параметров уравнения регрессии), n- число наблюдений.

Расчет значения F при n=30, m=2:

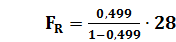= 27,888

Табличное (критическое) значение F-критерия F_табл имеет общий вид 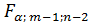, где 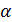- уровень значимости, m– число коэффициентов уравнения регрессии. При уровне значимости 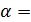0,05 и m=2

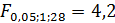
Так как F_расч>F_табл, то величина найденного коэффициента детерминации R^2.признается неслучайной с вероятностью 0,95.

Вывод. Построенное уравнение регрессии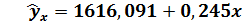

можно считать адекватным с надежностью 95%.