Изучение сегнетоэлектриков

1 Понятие о сегнетоэлектриках

2 Основные свойства сегнетоэлектриков

3 Точка Кюри

4 Связь вектора индукции с вектором поляризации

Основные понятия по теме

Сегнетоэлектрики – класс диэлектриков, которые обладают поляризованностью даже в отсутствии поля (спонтанная поляризованность). Диэлектрическая проницаемость ( 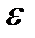) зависит от напряженности Е электрического поля, и при некоторых значениях напряженности относительная диэлектрическая проницаемость 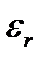принимает очень большие значения ( 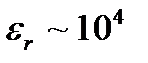). Характерными примерами сегнетоэлектриков являются такие химические соединения, как сегнетова соль NaKC₄HO₆·4H₂O, титанат бария BaTiO₃ и другие.

Сегнетоэлектрики представляют собой разновидность полярных диэлектриков, молекулы которых вследствие асимметрии их строения обладают дипольными моментами даже в отсутствие внешнего электрического поля. В обычных полярных диэлектриках дипольные моменты различных молекул в отсутствие внешнего электрического поля ориентированы хаотически из-за теплового движения молекул. Поэтому суммарный дипольный момент молекул в любом физически бесконечно малом объеме равен нулю. В сегнетоэлектриках имеет место сильное взаимодействие между дипольными моментами молекул, характерная энергия которого превышает энергию хаотического теплового движения молекул. Вследствие этого взаимодействия, дипольные моменты близких молекул ориентируются в одном направлении, то есть происходит самопроизвольная поляризация сегнетоэлектрика в отсутствие внешнего электрического поля. Область сегнетоэлектрика, в пределах которой все дипольные моменты ориентированы в одном направлении, называется сегнетоэлектрическим доменом. Сильная спонтанная поляризация такого домена приводит к возникновению в окружающем пространстве электрического поля. Минимизация энергии внешнего электрического поля достигается благодаря поляризации доменов в различных направлениях. В этом случае суммарный дипольный момент всего сегнетоэлектрика и напряженность электрического поля в окружающем пространстве близки к нулю. Принимая во внимание доменную структуру сегнетоэлектриков, можно качественно объяснить их диэлектрические свойства. При помещении сегнетоэлектрика во внешнее электрическое поле возникает взаимодействие с этим полем. 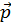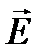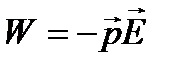Поскольку потенциальная энергия дипольного момента в электрическом поле с напряженностью равна и имеет минимум при параллельной ориентации векторов 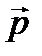и 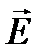, то по мере возрастания напряженности поля будет происходить постепенная поляризация доменов в направлении внешнего электрического поля. Приблизительный график зависимости электрического поля показан на рисунке 2.1.

P

Pнас

ε0Eкр

ε0E

Рисунок 2.1 – График зависимости поляризации сегнетоэлектрика

от напряженности электрического поля

На рисунке 2.1 P –поляризация сегнетоэлектрика, P_нас – насыщенное значение поляризации сегнетоэлектрика, 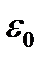– электрическая постоянная, E – напряженность электрического поля, E_кр – критическое значение напряженности электрического поля, физический смысл которого будет выяснен ниже (рисунок 2.3).Рисунок 2.1 показывает, что в точке, соответствующей критическому значению напряженности электрического поля, касательная к кривой P( 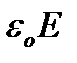) проходит через начало координат.

Кривая имеет горизонтальный участок, соответствующий состоянию насыщения поляризации 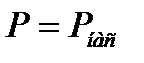. В этом состоянии весь объем сегнетоэлектрика поляризован в направлении внешнего электрического поля, и при возрастании напряженности не может происходить дальнейшее увеличение поляризации. Что касается электрической индукции

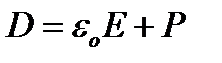, (2.1)

то состоянию насыщения поляризации сегнетоэлектрика (P = const) соответствует линейная зависимость между величинами D и E. Значение P_нас можно определить путем экстраполяции линейного участка кривой D( 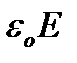), образующего с осью абсцисс угол 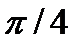, до пересечения с осью ординат. При этом длина отрезка, отсекаемого прямой на оси ординат, равна P_нас (рисунок 2.2).

D

Pнас

ε0E

Рисунок 2.2 – График зависимости электрической индукции

от напряженности поля

Поскольку в общем случае имеет место нелинейная зависимость электрической индукции D от напряженности поля E, то относительная диэлектрическая проницаемость 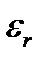является функцией E. Из (2.1) следует зависимость

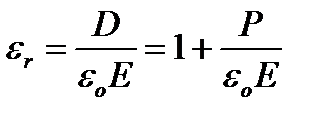, (2.2)

график которой представлен на рисунке 2.3.

εr

E

Eкр

Рисунок 2.3 – График зависимости относительной диэлектрической проницаемости от напряженности поля

В соответствии с рисунком 2.1, при малых значениях E поляризация быстро растет, а относительная диэлектрическая проницаемость увеличивается. При больших напряжённостях рост поляризации замедляется, и 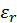, достигнув максимального значения, начинает монотонно убывать. После перехода сегнетоэлектрика в состояние насыщения поляризации относительная диэлектрическая проницаемость стремится к единице по гиперболическому закону

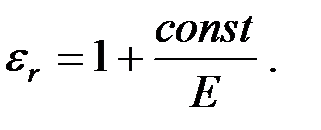
Таким образом, эффективное использование больших значений 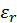возможно только при определенных напряженностях электрического поля, когда сегнетоэлектрик еще не находится в состоянии насыщения поляризации. Напряженность E_кр, при которой относительная диэлектрическая проницаемость 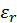имеет максимальное значение, можно определить из условия 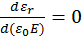. Используя выражение (2.1), (2.2), получаем соотношения:

, ,

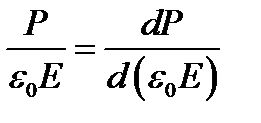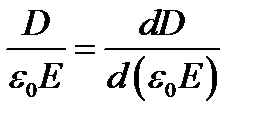означающие, что в точке, соответствующей критическому значению напряженности электрического поля, касательные к кривым P( 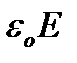) и D( 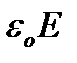) проходят через начало координат. При уменьшении напряженности значения электрической индукции поляризованного сегнетоэлектрика изменяются медленнее, чем это происходило при первоначальной поляризации образца (рисунок 2.4).

Это связано со свойством доменов частично сохранять прежнее направление поляризации. Значение P_r характеризует остаточную поляризацию сегнетоэлектрика при полном выключении электрического поля. Для того, чтобы ликвидировать остаточную поляризацию образца, необходимо приложить электрическое поле в противоположном направлении.

Длина отрезка 0E_c пропорциональна напряженности поля, необходимого для полной деполяризации сегнетоэлектрика. При дальнейшем увеличении E происходит поляризация образца в противоположном направлении, и в случае гармонического изменения напряженности поля зависимость P(E) имеет вид замкнутой кривой, изображенной на рисунке 2.4. Эта кривая называется петлей гистерезиса.

Как следует из рисунка 2.4, зависимость индукции и относительной диэлектрической проницаемости 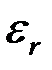от напряженности поля является неоднозначной, и на состояние сегнетоэлектрика при некотором значении напряженности влияют предшествующие значения E. Явление гистерезиса можно наблюдать с помощью установки, принципиальная схема которой представлена на рисунке 2.5.

А

В

Ес

Рr

Рн

Р

С

ε0Е

Рисунок 2.4 – Петля гистерезиса

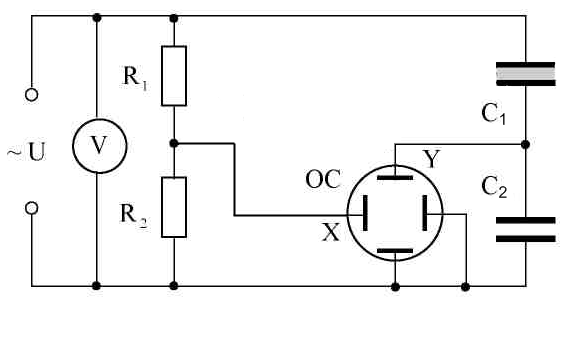
Рисунок 2.5 – Принципиальная схема установки

Переменное напряжение ~110 В подводится от источника питания на делитель, состоящий из сопротивлений R₁и R₂. Параллельно делителю включены две последовательно соединённые ёмкости: исследуемый конденсатор C₁ , заполненный сегнетоэлектриком, и эталонный C₂.

Величина подаваемого переменного напряжения регулируется переменным резистором (ручка на лицевой панели кассеты). При подаче напряжения в электрическую цепь обеспечивается поляризуемость сегнетокерамического конденсатора C₁ – диэлектрический гистерезис.

Напряжение на сопротивлении R₂, подаваемое на горизонтально отклоняющие пластины осциллографа (вход Х), U_x является пропорциональным полному напряжению U

На вертикально отклоняющие пластины осциллографа (вход Y) напряжение U₂ подается непосредственно с эталонного конденсатора C₂ (U_y).

При синусоидальном изменении внешнего напряжения электронный луч прочертит на экране осциллографа кривую, абсцисса и ордината точек которой пропорциональны соответственно величинам 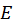и P.

Используя определение емкости конденсатора

,

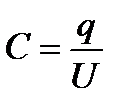и учитывая, что при последовательном соединении конденсаторов их заряды одинаковы, получаем:

.

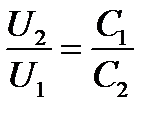Поскольку емкость эталонного конденсатора C₂ значительно превышает емкость конденсатора С₁, заполненного сегнетоэлектриком, то выполняются соотношения

U₁ >> U₂,

U₁ = U – U₂ ≈ U.

Используя формулу для определения напряженности электрического поля, получим

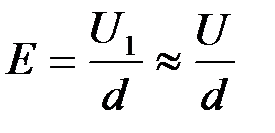, (2.3)

или

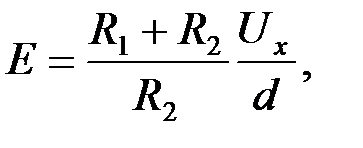(2.3.1)

где d – толщина сегнетоэлектрика.

Индукция D электрического поля определяется по формуле

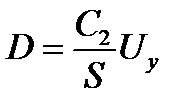, (2.4)

где S – площадь пластины сегнетоэлектрика.

Учитывая формулы (2.3) и (2.4), диэлектрическую проницаемость 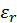находим по формуле

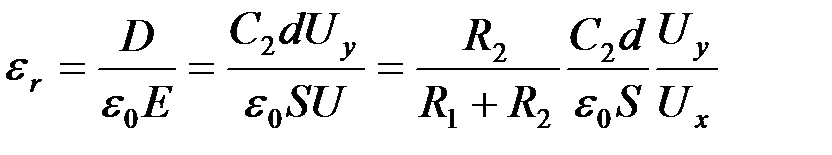, (2.5)

Рассмотренные свойства сегнетоэлектриков проявляются лишь при определенных температурах. При нагревании образца взаимодействие дипольных моментов молекул ослабляется, и при некоторой температуре Т_0, называемой температурой Кюри, происходит разрушение доменов. Спонтанная поляризация образца исчезает, и он из сегнетоэлектрика превращается в обычный диэлектрик. При температурах, незначительно превышающих температуру Кюри, диэлектрическая проницаемость образца быстро убывает в соответствии с законом Кюри-Beйсca

,

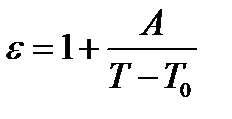где А – постоянная.

Некоторые образцы имеют также нижнюю точку Кюри T₀^′, и их сегнетоэлектрические свойства проявляются только в интервале температур T₀^′ < T < T₀. В этом случае зависимость диэлектрической проницаемости от температуры при T < T₀^′ имеетследующий вид:

.

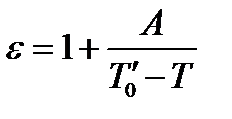Магнитные свойства ферромагнетиков – веществ, способных сильно намагничиваться, полностью аналогичны рассмотренным электрическим свойствам сегнетоэлектриков. Все результаты и выводы, полученные в данном разделе, остаются справедливыми также и для ферромагнетиков после формальной замены во всех соотношениях 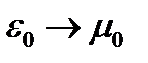, , 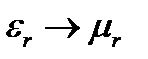, , 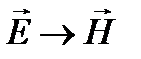, 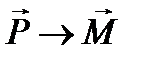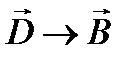где 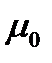– магнитная постоянная, 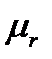– относительная магнитная проницаемость вещества, 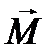– вектор намагниченност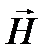и, и 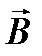– векторы напряженности и индукции магнитного поля.

Вопросы для самоконтроля

1 Поясните механизм поляризуемости диэлектриков при наложении внешнего электрического поля.

2 Назовите свойства сегнетоэлектриков. Что такое домены?

3 Объясните диэлектрический гистерезис. Приведите определение диэлектрической проницаемости и других параметров сегнетоэлектриков.

4 Приведите зависимость поляризации, электрической индукции и относительной диэлектрической проницаемости сегнетоэлектрика от напряженности электрического поля.

Лабораторная работа 2