Линейные операции над матрицами
Суммой матриц А и В условимся называть такую матрицу, элементы которой равны сумме соответствующих элементов матриц А и В. Складывать можно только матрицы, имеющие одинаковое строение: или прямоугольные типа т×п , или квадратные порядка п.
Пусть А = 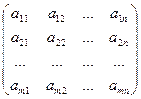 , B =
, B = 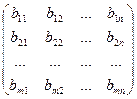 .
.
Тогда сумма матриц С = А + В имеет вид
С = 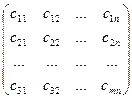 ,
,
где c11 = a11 + b11, c12 = a12 + b12, … cij = aij + bij, …, cmn = amn + bmn.
1. Сложить матрицы А и В, если: а) А = 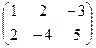 , В = , В = 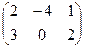 ; б) А = ; б) А = 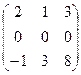 , В = , В = 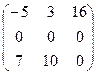 ; в) А = ; в) А = 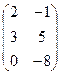 , В = , В = 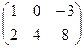 . Р е ш е н и е: а) Здесь А и В – прямоугольные матрицы типа 2 × 3. Складываем их соответствующие элементы: С = А + В = . Р е ш е н и е: а) Здесь А и В – прямоугольные матрицы типа 2 × 3. Складываем их соответствующие элементы: С = А + В = 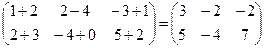 . б) Здесь А и В – квадратные матрицы третьего порядка. Складываем их соответствующие элементы: С = А + В = . б) Здесь А и В – квадратные матрицы третьего порядка. Складываем их соответствующие элементы: С = А + В = 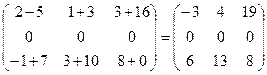 . В) Эти прямоугольные матрицы сложить нельзя, т.к. А есть матрица типа 3×2, а В – матрица типа 2×3; можно складывать только прямоугольные матрицы одного типа. . В) Эти прямоугольные матрицы сложить нельзя, т.к. А есть матрица типа 3×2, а В – матрица типа 2×3; можно складывать только прямоугольные матрицы одного типа. |
Из выше изложенного следует, что сложение матриц сводится непосредственно к сложению их элементов, являющихся числами. Поэтому на сложение матриц распространяются важнейшие свойства чисел:
1) переместительный закон сложения: А + В = В + А, где А и В – либо квадратные матрицы одного порядка п, либо прямоугольные матрицы одного типа т×п;
2) сочетательный закон сложения: (А + В) + С = А + (В + С), где А, В и С - либо квадратные матрицы одного порядка п, либо прямоугольные матрицы одного типа т×п;
Для любой матрицы А существует матрица – А, такая, что А + (- А) = 0, т.е. матрица, противоположная А.
Произведением матрицы А на число k называется такая матрица kA, каждый элемент которой kaij, т.е. если А = 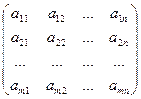 , то kA =
, то kA = 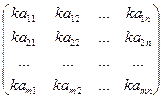 .
.
Умножение матрицы на число сводится к умножению на это число всех элементов матрицы.
2. Умножить матрицу А = 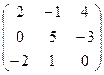 на число k = 3. Р е ш е н и е. 3А = на число k = 3. Р е ш е н и е. 3А = 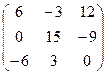 . 3. Найти матрицу, противоположную матрице А = . 3. Найти матрицу, противоположную матрице А = 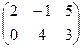 . Р е ш е н и е . Для нахождения противоположной матрицы умножаем матрицу А на k = -1. - А = . Р е ш е н и е . Для нахождения противоположной матрицы умножаем матрицу А на k = -1. - А = 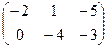 . 4. Найти линейную комбинацию 3А – 2В, если А = . 4. Найти линейную комбинацию 3А – 2В, если А = 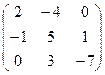 , В = , В = 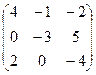 . Р е ш е н и е. Сначала находим произведение А на k1 = 3 и k2 = -2. 3А = . Р е ш е н и е. Сначала находим произведение А на k1 = 3 и k2 = -2. 3А = 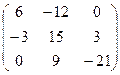 , -2В = , -2В = 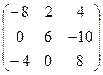 . Теперь найдем сумму полученных матриц: 3А – 2В = . Теперь найдем сумму полученных матриц: 3А – 2В = 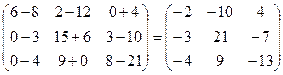 . . |
- Умножение матриц
Рассмотрим умножение квадратных матриц второго порядка. Пусть
А = 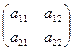 , B =
, B = 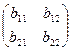 .
.
Произведением этих матриц называется матрица
С = АВ = 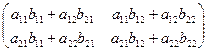 .
.
Чтобы найти элемент с11 первой строки и первого столбца матрицы С, нужно каждый элемент первой строки матрицы А (т.е. а11 и а12) умножить на соответствующий элемент первого столбца матрицы В (т.е. b11 и b21) и полученные произведения сложить: c11 = a11b11 + a12b21.
Вообще, чтобы получить элемент, стоящий на пересечении i – той строки и j – того столбца матрицы-произведения, нужно все элементы i – той строки (аi1, аi2, …, аin) матрицы А умножить на соответствующие элементы j – того столбца (b1j, b2j, …, bnj) матрицы B и полученные произведения сложить.
5. Найти произведение матриц А и В, если А = 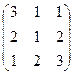 , В = , В = 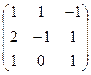 . Р е ш е н и е. Найдем каждый элемент матрицы-произведения: c11 = a11b11 + a12b21 + a13b31 = 3·1 + 1·2 + 1·1 = 6; c12 = a11b12 + a12b22 +a13b32 = 3·1 + 1·(-1) + 1·0 = 2; c13 = a11b13 + a12b23 + a13b33 = 3·(-1) + 1·1 + 1·1 = -1; c21 = a21b11 +a22b21 + a23b31 = 2·1 + 1·2 + 2·1 = 6; c22 = a21b12 + a22b22 +a23b32 = 2·1 + 1·(-1) + 2·0 = 1; c23 = a21b13 +a22b23 +a23b33 = 2·(-1) + 1·1 + 2·1 = 1; c31 = a31b11 + a32b21 + a33b31 = 1·1 + 2·2 + 3·1 = 8; c32 = a31b12 + a32b22 + a33b32 = 1·1 + 2·(-1) + 3·0 = -1; c33 = a31b13 + a32b23 + a33b33 = 1·(-1) + 2·1 + 3·1 = 4. Следовательно, С = . Р е ш е н и е. Найдем каждый элемент матрицы-произведения: c11 = a11b11 + a12b21 + a13b31 = 3·1 + 1·2 + 1·1 = 6; c12 = a11b12 + a12b22 +a13b32 = 3·1 + 1·(-1) + 1·0 = 2; c13 = a11b13 + a12b23 + a13b33 = 3·(-1) + 1·1 + 1·1 = -1; c21 = a21b11 +a22b21 + a23b31 = 2·1 + 1·2 + 2·1 = 6; c22 = a21b12 + a22b22 +a23b32 = 2·1 + 1·(-1) + 2·0 = 1; c23 = a21b13 +a22b23 +a23b33 = 2·(-1) + 1·1 + 2·1 = 1; c31 = a31b11 + a32b21 + a33b31 = 1·1 + 2·2 + 3·1 = 8; c32 = a31b12 + a32b22 + a33b32 = 1·1 + 2·(-1) + 3·0 = -1; c33 = a31b13 + a32b23 + a33b33 = 1·(-1) + 2·1 + 3·1 = 4. Следовательно, С = 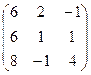 . . |
Правило нахождения матрицы-произведения распространяется на умножение прямоугольных матриц.
6. Найти произведение АВ, если А = 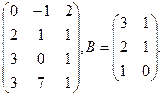 Р е ш е н и е. АВ = Р е ш е н и е. АВ = 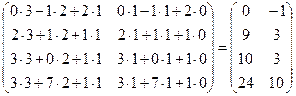 |
Если в этом примере мы попытаемся найти произведение ВА, то убедимся, что это невозможно.
Для прямоугольных матриц справедливы следующие правила:
1) умножение матрицы А на матрицу В имеет смысл только в том случае, когда число столбцов матрицы А равно числу строк матрицы В;
2) в результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк в первой матрице, и столько столбцов, сколько столбцов во второй матрице.
- Свойства умножения матриц
Пусть А = 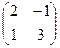 , В =
, В = 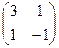 . Найдем произведения АВ и ВА:
. Найдем произведения АВ и ВА:
АВ = 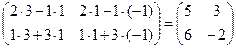
ВА = 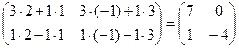 .
.
Видно, что АВ≠ВА. Этот пример показывает, что произведение двух матриц, вообще говоря, не подчиняется переместительному закону.
Можно проверить, что для умножения матриц выполняется сочетательный и распределительный законы умножения: А(ВС) = (АВ С, (А +В)С = АВ + ВС.
Отметим следующий любопытный факт. Известно, что произведение двух, отличных от нуля чисел, не равно нулю. Для матриц это не всегда справедливо, т.е. возможен случай, когда произведение двух ненулевых матриц может оказаться равным нулевой матрице. Например, если А = 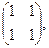 В =
В = 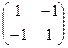 , то
, то
АВ = 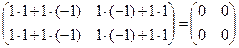 .
.
