Канонічне та параметричне рівняння прямої

Нехай в системі координат 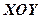задана точка 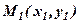і ненульовий вектор 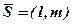(рис.7).

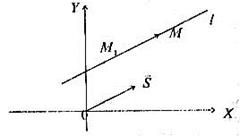
рис.7.

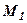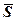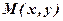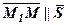Необхідно скласти рівняння прямої, що проходить через точку паралельно вектору , що називається напрямним вектором. Довільна точка належить цій прямій тоді і тільки тоді, коли . Оскільки вектор 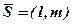– заданий, а вектор 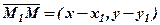, то згідно з умовою паралельності, координати цих векторів пропорційні, тобто

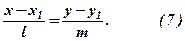
Співвідношення (7) називається рівнянням прямої, що проходить через задану точку у заданому напрямку або канонічним рівнянням прямої.

Звернемо увагу, що до рівняння вигляду (7) можна перейти, наприклад, від рівняння пучка прямих(4)

,

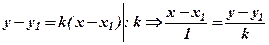або від рівняння прямої за точкою та нормальним вектором (1)

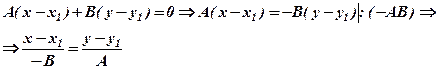
Зауваження. Вище припускалось, що напрямний вектор 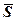– ненульовий, але може трапитись, що одна з його координат, наприклад, 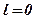. Тоді вираз (7) формально запишеться

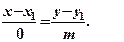
який, взагалі кажучи, не має смислу. Однак приймають 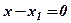і отримують рівняння прямої перпиндикулярної осі 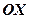. Дійсно із рівності видно, що пряма визначена точкою 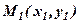і напрямним вектором 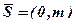, перпиндикулярним осі 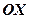. Якщо ж в цьому рівнянні звільнитись від знаменника, то отримаєм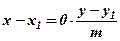о , або 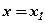– рівняння прямої, перпендикулярної осі 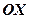. Аналогічно було б отримано 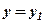для вектора .

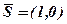Щоб перейти до параметричного рівняння прямої, прирівняємо кожен із дробів (7) до параметра 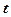. Оскільки хоча б один із знаменників в (7) відмінний від нуля, а відповідний чисельник може набувати довільні значення, то область зміни параметра 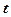– вся числова вісь. Отримаємо

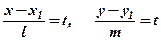або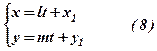

Рівняння (8) називається параметричним рівнянням прямої.