Производные основных элементарных функций
I Степенная функцияy=xa
Находим приращение функции и составляем разностное отношение:
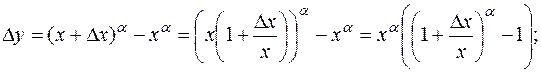
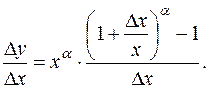
Вычислим предел этого разностного отношения, используя эквивалентность для степенной функции 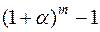 ~ ma при
~ ma при 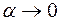 :
:
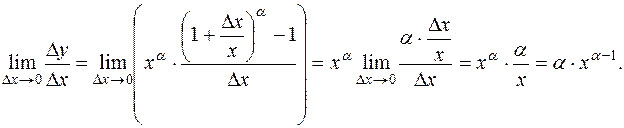 Итак, имеем
Итак, имеем
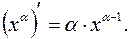 (1)
(1)
Замечание 1. Вывод последней формулы предполагает, что 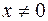 . Вычис-лим
. Вычис-лим 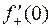 (считаем, что
(считаем, что 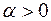 , следовательно,
, следовательно, 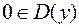 ):
):
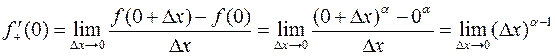 .
.
Величина этого предела зависит от 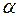 : для
: для 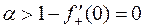 , для
, для 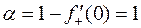 и для
и для 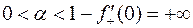 . Но этот же результат можно получить из формулы (1) с помощью теоремы 2 §3. Аналогичный результат можно получить и для
. Но этот же результат можно получить из формулы (1) с помощью теоремы 2 §3. Аналогичный результат можно получить и для 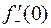 , если a таково, что степенная функция определена для
, если a таково, что степенная функция определена для 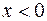 .
.
Замечание 2. Ряд частных случаев формулы (1) лучше запомнить как самостоятельные формулы дифференцирования:
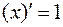 ,
, 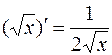 ,
, 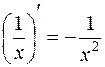 .
.
II Показательная функцияy=ax
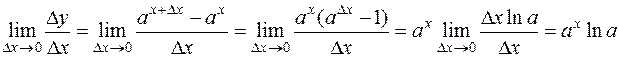 .
.
Итак,
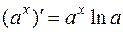 .
.
Частный случай этой формулы: 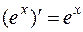 .
.
III Логарифмическая функция 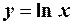
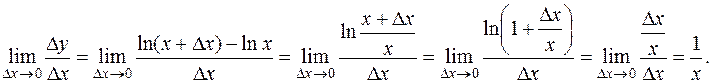 Итак,
Итак,
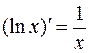 .
.
Для логарифмической функции с произвольным основанием используем формулу перехода:
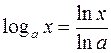 .
.
Отсюда 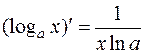 .
.
Можно предложить и другой способ вычисления 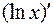 с использованием основного логарифмического тождества
с использованием основного логарифмического тождества 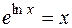 . Продифференцировав почленно это тождество, получим:
. Продифференцировав почленно это тождество, получим:
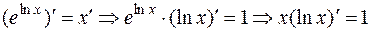 .
.
Отсюда и получим 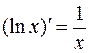 .
.
IV Тригонометрические функции
1. y=sinx
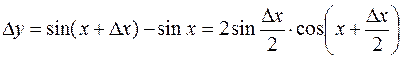 .
.
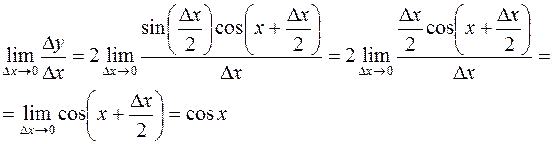
(на последнем шаге мы воспользовались непрерывностью косинуса).
Итак,
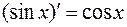 .
.
Производные остальных тригонометрических функций можно вычислить, используя определение производной, но проще использовать известные правила дифференцирования и формулы, связывающие тригонометрические функции друг с другом.
2. y=cosx
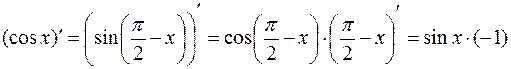 .
.
Итак,
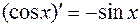 .
.
3. y=tgx
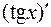
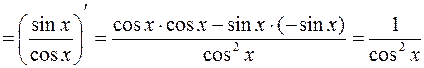 .
.
Итак,
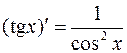 .
.
4. y=сtgx.
Аналогично предыдущему можно получить
(ctg 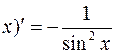 .
.
V Обратные тригонометрические функции
Производные этих функций проще всего получить при помощи основного тождества, связывающего пару взаимно обратных функций, а именно: 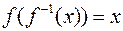 .
.
1. y=arcsinx
Дифференцируем почленно тождество 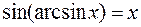 :
:
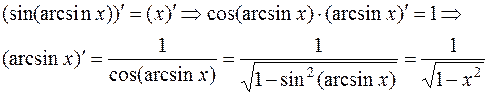
(напомним, что 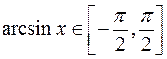 , поэтому
, поэтому 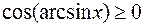 ).
).
Итак,
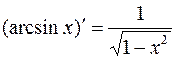 .
.
2. y=arccosx
Известное соотношение 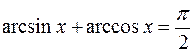 и предыдущая формула для
и предыдущая формула для 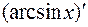 , позволяют получить
, позволяют получить
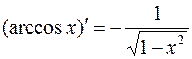 .
.
3. y=arctgx
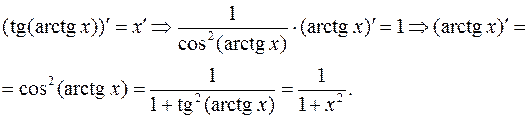
Итак,
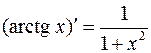 .
.
4. y=arcctgx
Из соотношения 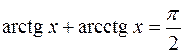 , получим
, получим 
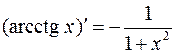 .
.
Замечание 3. Покажем на примере 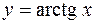 как можно получать производные аркфункций, исходя из определения производной. Приращение арктангенса
как можно получать производные аркфункций, исходя из определения производной. Приращение арктангенса 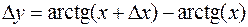 стремится к 0 при
стремится к 0 при  (в силу непрерывности функции). Отсюда получаем эквивалентность: при
(в силу непрерывности функции). Отсюда получаем эквивалентность: при 
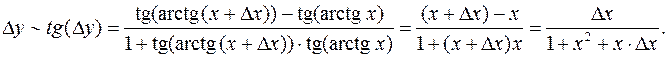 Теперь можно легко найти предел разностного отношения:
Теперь можно легко найти предел разностного отношения:
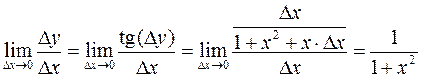 .
.
Замечание 4. Производные аркфункций можно получить также, используя общее правило дифференцирования обратной функции, которое будет приведено ниже.
VI Гиперболические и обратные гиперболические функции
Эти функции элементарным образом выражаются через показательную и логарифмическую функции. Поэтому проще всего находить их производные, используя известные правила дифференцирования.
Например:
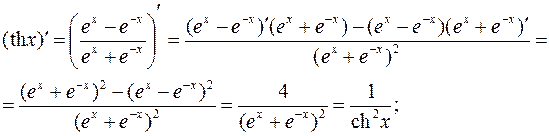
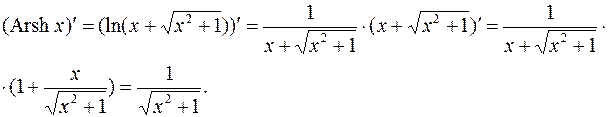
Производные других функций этой группы студентам предлагается получить самостоятельно.
VII Сводка формул для производных
1. 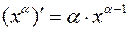 ,
, 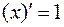 ,
, 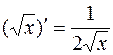 ,
, 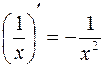 .
.
2. 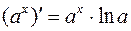 ,
, 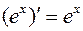 .
.
3. 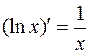 ,
, 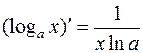 .
.
4. 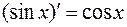 . 5.
. 5. 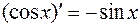 .
.
6. (tg 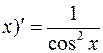 . 7. (ctg
. 7. (ctg 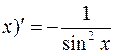 .
.
8. 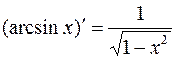 . 9.
. 9. 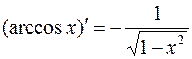 .
.
10. 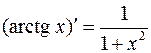 . 11.
. 11. 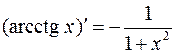 .
.
12. 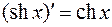 . 13.
. 13. 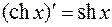 .
.
14. 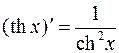 . 15.
. 15. 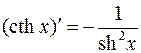 .
.
16. 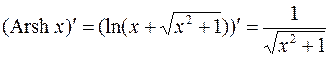 .
.
17. 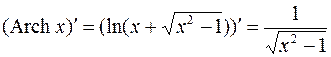 .
.
18. 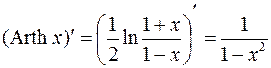 .
.
