Запишите решение заданий уровня B с полным обоснованием. В1.Найдите значение , если f(x) = sin 4x·cos 4x
В1.Найдите значение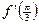 
, если f(x) = sin 4x·cos 4x.
В2.Функция у = f(x) задана на промежутке (-5;7). График ее производной y=f´(x) изображен на рисунке. Сколько экстремумов имеет функция y=f(x) на промежутке(-5;7)?
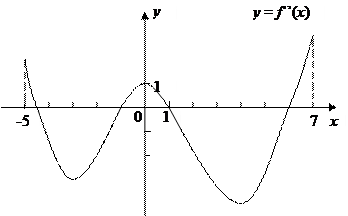
В3.Найдите длину промежутка убывания функции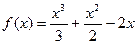 
.
Запишите решение заданий уровня C с полным обоснованием
С1.Прикаком наибольшем значении а функция f(x)=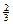 
x3 – ax2 + ax +7 возрастает на всей числовой прямой?
С2.Найдите множество значений функции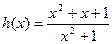 
.
Диагностическая контрольная работа
По алгебре и началам анализа.
«Производная функции. Приложения производной»
Вариант 23
Запишите вариант правильного ответа заданий уровня А
А1.Найдите производную функции: f(x)=21x3-15x2
| а) f′(x)=21x3-15x2 | б) f′(x)=21x2-15x | в) f′(x)=63x3-30x2 | г) f′(x)=63x2-30x |
А2.Найдите скорость изменения функции y=-5x+4
| а) -5 | б) 4 | в) -1 | г) 9 |
А3.Найдите значение производной в точке x0, если g(x)=cosx,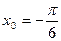 
а)  | б)  | в) 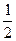 | г)  |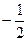
А4.Для какой из функций производная задается формулой y′=9x2-sinx?
| а) y=3x2-cosx | б) y=3x3+cosx | в) y=9x-cosx | г) y=x3+sinx |
А5.Определите промежутки возрастания функции y=f(x), если данные о ее производной f′(x) указаны в таблице.
| X | 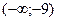 | -9 | (-9;-1) | -1 | (-1;3) |  | |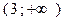
| f′ | + | - | + | - | |||
а) 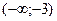 | б) 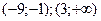 | в) 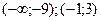 | г)  |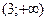
А6.Найдите угловой коэффициент касательной к графику функции y=6sinx+2cosx в точке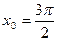 
| а) -2 | б) 2 | в) 6 | г) -6 |
А7.Тело движется по прямой, так что расстояние S от начальной точки изменяется по закону S=5t2-5t (м), где t – время в секунду. Найдите скорость тела через 2с после начала движения.
| а) 10 м/с | б) 15 м/с | в) 9 м/с | г) 11 м/с |
А8.Дана функция f(x)=2x2-x+1. Найдите координаты точки ее графика, в которой угловой коэффициент касательной к нему равен 7.
| а) (2;0) | б) (2;7) | в) (2;9) | г) (0;4) |
А9.Тело движется по прямой, так что расстояние S от начальной точки изменяется по закону S=6t-1,5t2, где t – время в секунду. В какой момент времени скорость будет равняться 2.
а) 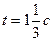 | б) t=3c | в) t=0,5c | г) t=5c |
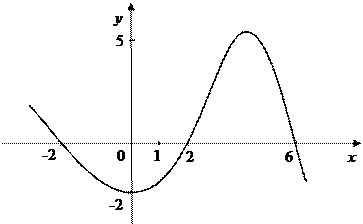А10.На рисунке изображен график производной функции y=f′(x). Найдите точку минимума функции y=f(x)
|
а) -2
б) 0
в) 2
г) 6
А11.Найдите производную функции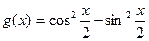 
| а) g′(x)=-sinx | б) g′(x)=cosx | в) g′(x)=sinx | г) иной ответ |
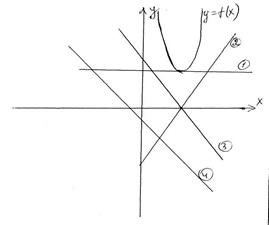
А12.Найдите график производной по графику функции y=f(x)
