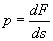Закон сохранения момента импульса. Уравнение моментов. Вращение твердого тела вокруг неподвижной оси.
 Пусть
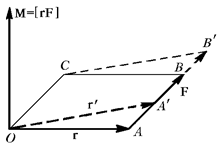
Пусть 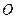 некоторая точка, относительно которой мы будем находить момент вектора силы или вектора импульса. Ее (точку) называют началом или полюсом.
некоторая точка, относительно которой мы будем находить момент вектора силы или вектора импульса. Ее (точку) называют началом или полюсом. 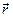 – вектор, проведенный из полюса к точке приложения силы. Момент силы
– вектор, проведенный из полюса к точке приложения силы. Момент силы 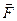 относительно точки
относительно точки 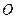 – произведение радиус-вектора
– произведение радиус-вектора 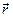 на силу
на силу 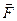 :
: 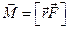 .
.
Момент 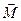 не изменится, если точку приложения силы
не изменится, если точку приложения силы 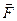 перенести в любую другую точку, расположенную на линии действия силы.
перенести в любую другую точку, расположенную на линии действия силы.
Момент 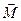 нескольких сил относительно точки – сумма моментов сил относительно той же точки. Момент силы
нескольких сил относительно точки – сумма моментов сил относительно той же точки. Момент силы 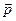 относительно точки
относительно точки 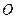 – произведение радиус-вектора
– произведение радиус-вектора 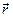 на импульс
на импульс 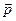 :
: 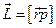 . Производная
. Производная 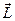 по времени будет выглядеть так:
по времени будет выглядеть так: 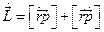 . Т.к.
. Т.к. 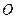 мы считаем неподвижной, то
мы считаем неподвижной, то 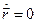 , а
, а 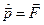 и мы получим
и мы получим 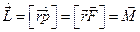 , т.е.
, т.е. 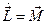 .
.
Последнее равенство – уравнение моментов.
Для системы материальных точек моменты всех внутренних сил равны нулю и мы можем записать уравнение моментов для множества материальных точек так: 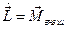 – производная момента импульса системы материальных точек по времени относительно неподвижного полюса равна геометрической сумме моментов всех внешних сил относительно того же полюса.
– производная момента импульса системы материальных точек по времени относительно неподвижного полюса равна геометрической сумме моментов всех внешних сил относительно того же полюса.
Закон сохранения момента импульса так же вытекает из этого уравнения – если сумма моментов всех внешних сил равна нулю относительно какого-то полюса, то момент импульса системы материальных точек относительно того же полюса будет постоянным во времени.
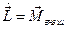 – эквивалентно
– эквивалентно 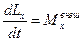 ,
, 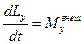 ,
, 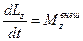 .
. 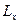 и
и 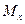 – моменты импульса и силы относительно оси
– моменты импульса и силы относительно оси 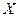 (проекции
(проекции 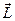 и
и 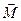 на эту ось ) .
на эту ось ) .
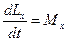 – уравнение моментов относительно неподвижной оси
– уравнение моментов относительно неподвижной оси 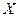 (предполагается, что начало
(предполагается, что начало 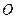 лежит на этой оси). Если момент всех внешних сил, относительно какой либо неподвижной оси равен нулю, то момент импульса относительно этой же оси будет постоянным. Пусть неподвижная ось – ось вращения, а материальная точка вращается вокруг нее по окружности с радиусом
лежит на этой оси). Если момент всех внешних сил, относительно какой либо неподвижной оси равен нулю, то момент импульса относительно этой же оси будет постоянным. Пусть неподвижная ось – ось вращения, а материальная точка вращается вокруг нее по окружности с радиусом  . Тогдамомент импульса относительно оси вращения равен
. Тогдамомент импульса относительно оси вращения равен 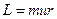 . Если
. Если 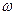 угловая скорость, то
угловая скорость, то 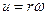 и
и 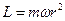 . Если же вокруг оси вращается система материальных точек с одинаковой угловой скоростью
. Если же вокруг оси вращается система материальных точек с одинаковой угловой скоростью  , то
, то 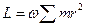 .
.
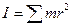 – момент инерции системы относительно оси. С учетом этого получаем
– момент инерции системы относительно оси. С учетом этого получаем 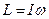 . Если же система материальных точек не только вращается, а принимает участие еще в каких то перемещениях (т.е.
. Если же система материальных точек не только вращается, а принимает участие еще в каких то перемещениях (т.е.  перестает быть постоянной), то уравнение трансформируется в соответствии с изменением мгновенной конфигурации системы:
перестает быть постоянной), то уравнение трансформируется в соответствии с изменением мгновенной конфигурации системы: 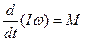 .
.
Оно является основном уравнением динамики вращательного движения вокруг неподвижной оси.
| Общие свойства жидких и газообразных тел | 1. Способность как угодно изменять свою форму под действием сколь угодно малых сил. 2. Жидкости и газы ведут себя как упругие тела в отношении деформации всестороннего сжатия и растяжения. 3. Для всякой площадки в жидкостях и газах существует только нормальное
4. Величина гидростатического давления в данной точке жидкости и газа одинакова для всех направлений площадки | |||
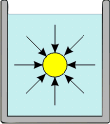
 Блез Паскаль (Pascal) (1623-1662) Закон Б. Паскаля (опублик. в 1663) Блез Паскаль (Pascal) (1623-1662) Закон Б. Паскаля (опублик. в 1663) | Давление на поверхности жидкости, произведённое внешними силами, перёдается жидкостью одинаково во всех направлениях. Иная формулировка этого закона: Давление в жидкости или газе перёдается во всех направлениях одинаково и не зависит от ориентации площадки, на которую оно действует. Для иллюстрации закона Паскаля изображена небольшая прямоугольная призма, погруженная в жидкость. Если предположить, что плотность материала призмы равна плотности жидкости, то призма должна находиться в жидкости в состоянии безразличного равновесия. Это означает, что силы давления, действующие на грани призмы, должны быть уравновешены. Это произойдет только в том случае, если давления, т.е. силы, действующие на единицу поверхности каждой грани, одинаковы: p1 = p2 = p3 = p. | 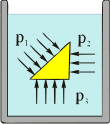 | ||
 Архимед (ок. 287-212 до н.э.) Закон Архимеда (III в. до н. э.) Архимед (ок. 287-212 до н.э.) Закон Архимеда (III в. до н. э.) | На всякое тело, погруженное в жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная весу вытесненной телом жидкости (или газа), направленная вертикально вверх и приложенная к центру тяжести вытесненного объема 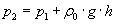 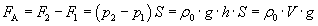 | 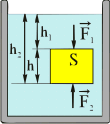 | ||
 Принцип отвердения Принцип отвердения  | ||||
Условие равновесия 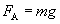 | 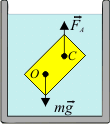  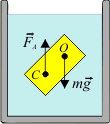 Устойчивое равновесие Устойчивое равновесие  Неустойчивое равновесие Неустойчивое равновесие | |||
| Барометрическая формула для изотермической атмосферы | 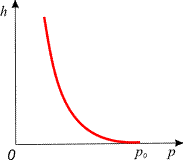 | 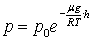 |
Гидро- и аэродинамика
| Основные понятия | Линии тока — линии, касательная к каждой точке которой указывает направление скорости потока. Стационарный поток — поток, при котором линии тока совпадают с траекториями отдельных частиц. Токовые трубки — поверхность, образованная линиями тока. Скорость жидкости (газа) во всех точках одного и того же сечения одинакова | |
| Модель | При стационарных течениях жидкости (и даже газы) можно считать несжимаемыми жидкостями, т.е. мы не пренебрегаем изменениями давлений, обусловленными изменениями степени сжатия, но пренебрегаем изменениями объема | |
Уравнение неразрывности струи  Даниил Бернулли (1700-1782) Уравнение Д. Бернулли (1738) Реактивное движение космического челнока Даниил Бернулли (1700-1782) Уравнение Д. Бернулли (1738) Реактивное движение космического челнока | 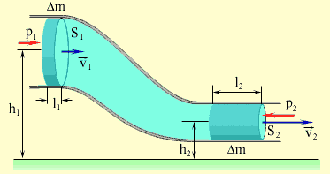  | 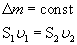 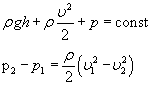 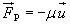 |
| Движение тел в жидкостях и газах | ||
Сопротивление трения 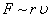 Сопротивление давления Сопротивление давления 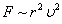 | 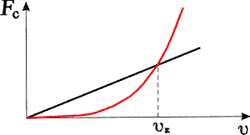 | 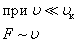 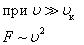 |
| Подъемная сила крыла самолета | 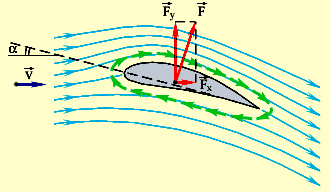 | Fy — подъемная сила Fx — сила лобового  сопротивления α — угол атаки сопротивления α — угол атаки |
Упругие идеально тела
Все реальные тела деформируемы. Под действием приложенных сил они меняют свою форму или объем. Такие изменения называются деформациями. В случае твердых тел различают два предельных случая: деформации упругие и деформации пластические.
 Упругими называют деформации, исчезающие после прекращения действия приложенных сил.
Упругими называют деформации, исчезающие после прекращения действия приложенных сил.
Пластическими или остаточными деформациями называют такие деформации, которые сохраняются в теле, по крайней мере частично, и после прекращения действия внешних приложенных сил. На пластических деформациях основана холодная обработка металлов − штамповка, ковка и пр.
Является ли деформация упругой или пластической зависит не только от материала тела, но и от приложенных сил. Если сила (точнее, сила, отнесенная к единице площади, т. е. напряжение) не превосходит известной величины, называемой пределом упругости, то возникающая деформация будет упругой. Если же она превосходит этот предел, то возникающая деформация будет пластической.
Предел упругости имеет различные значения для разных материалов. Она является не вполне четкой определенной величиной. Разделение тел на упругие и пластические также в какой-то степени условно. Строго говоря, все деформации после прекращения действия внешних сил исчезают не полностью, а поэтому являются пластическими. Однако если остаточные деформации малы, то во многих случаях их можно не принимать во внимание. Как велика должна быть остаточная деформация, чтобы можно было так поступать, зависит от конкретных условий. В некоторых случаях, например, можно пренебречь остаточными деформациями, если они не превосходят 0,1 % от максимальных значений, достигавшихся под действием приложенных сил. В других случаях этот предел должен быть снижен до 0,01 % и т. д.
Механика описывает упругие свойства тел посредством некоторых эмпирически вводимых упругих постоянных, различных для различных тел и зависящих от их физического состояния (например, от температуры). Более глубоким является физический подход, рассматривающий явление деформаций с атомистической точки зрения. Этим занимается теория твердого тела.
Она позволяет в принципе не только вывести основные уравнения механики деформируемых тел с атомистической точки зрения, но и установить связь между упругими постоянными вещества и другими его физическими свойствами.
Тела мы будем считать идеально упругими. Так называются идеализированные тела, которые могут претерпевать только упругие, но не пластические деформации. Такими идеализациями можно пользоваться, когда силы, приложенные к реальным телам, не превосходят предела упругости.
Для идеально упругих тел существует однозначная зависимость между действующими силами и вызываемыми ими деформациями.
В случае пластических деформаций такой однозначной связи не существует. Это видно хотя бы из того, что до и после пластической деформации тело имеет различную форму, хотя в обоих случаях оно не подвергается действию внешних сил.
Малыми называются упругие деформации, подчиняющиеся закону Гука. Это приближенный закон, согласно которому деформации пропорциональны силам, их вызывающим.
Твердые тела разделяются на изотропные и анизотропные.
Изотропными называются тела, свойства которых по всем направлениям одинаковы. Анизотропными называются тела, свойства которых в разных направлениях не одинаковы.
Типичными представителями анизотропных тел являются кристаллы. Приведенные определения отличаются некоторой неопределенностью, поскольку в них явно не указано, о каких физических свойствах идет речь. Дело в том, что тела могут вести себя как изотропные по отношению к одним свойствам и как анизотропные − по отношению к другим. Так, все кристаллы кубической системы ведут себя как изотропные, если речь идет о распространении света в них. Однако они будут анизотропными, если интересоваться их упругими свойствами.
Металлы обычно имеют поликристаллическую структуру, т. е. состоят из мельчайших беспорядочно ориентированных кристалликов. Каждый из таких кристалликов есть тело анизотропное. Но кусочек металла, содержащий множество их, ведет себя как изотропное тело, если всевозможные ориентации кристалликов представлены с одинаковой вероятностью. В результате пластической деформации хаотичность в ориентации кристалликов может нарушиться. Тогда после пластической деформации металл становится анизотропным. Такое явление наблюдается, например, при вытягивании или кручении проволоки.
УПРУГАЯ ДЕФОРМАЦИЯ
изменение формы и размеров элемента конструкции, возникающее под действием нагрузки и исчезающее после ее снятия. В материалах инженерных конструкций (металл, дерево, бетон, железобетон, камень) У. д. получаются, если напряжения в элементах конструкции не выходят за определенные пределы. У. д. тем больше, чем больше действующая на элемент нагрузка, чем меньше площади или моменты инерции сечений элемента и чем ниже модуль упругости того материала, из к-рого выполнен элемент.
Твердые тела под действием внешних сил деформируются, т.е. изменяют форму или объем. Тела, которые после прекращения действия внешних сил полностью восстанавливают свои первоначальные размеры и форму, называются упругими, а такие деформации -- упругими. Упругие деформации происходят в том случае, если сила, вызвавшая деформацию, не превосходит некоторой, определенной для каждого конкретного тела (материала), величины.
Если тело после устранения внешней силы остается полностью деформированным, оно является абсолютна неупругим (пластичным).
При деформации тел в них возникают внутренние силы. В упругих телах они определяются величиной и видом деформации и после прекращения действия внешних сил возвращают телу его первоначальные размеры и форму.
Существует множество видов упругих деформаций: одностороннее растяжение (и сжатие), всестороннее растяжение (и сжатие), изгиб, сдвиг, кручение н др. Любую упругую деформацию можно свести к двум основным: растяжению (или сжатию) и сдвигу.
Основные закономерности упругих деформаций были сформулированы английским физиком Робертом Гуком в 1675 году. Закон, носящий его имя, заключается в следующем:
- при любой малой деформации сила упругости пропорциональна деформации,
- малые деформации пропорциональны приложенным силам.
Получим математическое выражение для этого закона применительно к деформации однородного растяжения, которая изучается в данной работе.
Пусть к тонкому стержню (проволоке) длиной 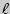 , один конец которого закреплен, приложена внешняя растягивающая сила
, один конец которого закреплен, приложена внешняя растягивающая сила 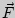 . Стержень получил некоторое абсолютное удлинение
. Стержень получил некоторое абсолютное удлинение 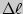 . Количественной характеристикой деформации может служить
. Количественной характеристикой деформации может служить 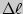 или относительное удлинение
или относительное удлинение 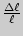 , называемое также в общем случае относительной деформацией.
, называемое также в общем случае относительной деформацией.
Относительное удлинение -- отвлеченное число, указывающее, на какую часть увеличилась первоначальная длина стержня. Существует понятие однородной деформации, при которой каждый элемент стержня произвольной длины 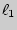 имеет такое же относительное удлинение, как и весь стержень:
имеет такое же относительное удлинение, как и весь стержень:
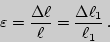
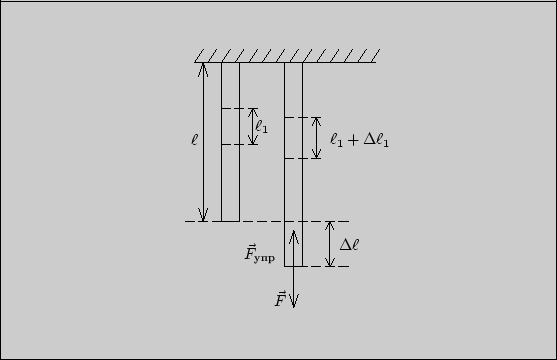
Рис. 1
Таким образом, 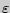 - количественная характеристика деформации
- количественная характеристика деформации
как всего стержня, так и любой его части, т.е. исчерпывающая характеристика однородной упругой деформации.
Сила упругости 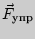 , возникающая в растянутом стержне, оценивается по внешней растягивающей силе
, возникающая в растянутом стержне, оценивается по внешней растягивающей силе 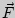 . Из условия равновесия стержня имеем:
. Из условия равновесия стержня имеем:
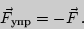 | (1) |
Силы упругости действуют в любом сечения стержня и при однородной статической деформации повсюду одинаковы и равны по модулю внешней растягивающей силе.
Деформации, независящие от времени, называются стационарными. При этом стационарные деформации покоящегося или равномерно движущегося тела называются статическими.
Р.Гук на опыте установил, что абсолютное удлинение в случае малых деформаций прямо пропорционально первоначальной длине стержня и растягивающей силе и обратно пропорционально его площади поперечного сечения 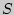 :
:
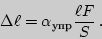 | (2) |
Коэффициент пропорциональности 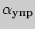 зависит от рода материала и является характеристикой его упругих свойств. Это коэффициент упругости, определяемый на опыте, а для некоторых тел рассчитываемый теоретически из молекулярных представлений.
зависит от рода материала и является характеристикой его упругих свойств. Это коэффициент упругости, определяемый на опыте, а для некоторых тел рассчитываемый теоретически из молекулярных представлений.
Величина, обратная коэффициенту упругости, называется модулем Юнга:
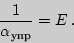 | (3) |
Для относительной деформации из выражения (2) имеем:
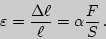 | (4) |
Отношение 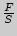 называется упругим напряжением
называется упругим напряжением 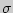 . Смысл выражения (4) -- относительная деформация прямо пропорциональна упругому напряжению:
. Смысл выражения (4) -- относительная деформация прямо пропорциональна упругому напряжению:
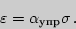 | (5) |
С помощью модуля Юнга можно иначе сформулировать и записать математически закон Гука:
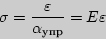 | (6) |