Невырожденные линейные операторы. Теорема о взаимной однозначности
Определение. Линейный оператор 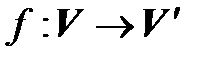 называется невырожденным, если он любой ненулевой вектор переводит в ненулевой.
называется невырожденным, если он любой ненулевой вектор переводит в ненулевой.
Теорема 4.4. Для того чтобы линейный оператор 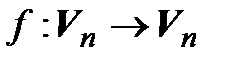 был невырожденным, необходимо и достаточно, чтобы он был взаимно однозначным.
был невырожденным, необходимо и достаточно, чтобы он был взаимно однозначным.
►Пусть 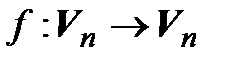 – линейный оператор, А – его матрица в некотором базисе, X и Y – координатные столбцы в том же базисе векторов
– линейный оператор, А – его матрица в некотором базисе, X и Y – координатные столбцы в том же базисе векторов 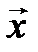 и
и 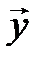 соответственно. Тогда
соответственно. Тогда
{ 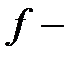 невырожденный}
невырожденный} 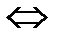
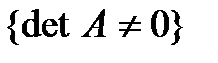
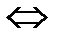 {
{ 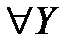 система
система 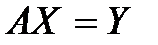 имеет единственное решение}
имеет единственное решение} 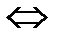 {
{ 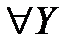
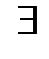 единственный
единственный 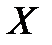 , что
, что 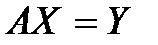 }
} 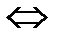
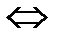 {
{ 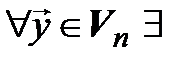 единственный
единственный 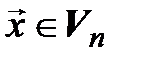 , что
, что 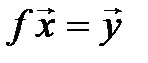 }
} 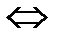 {f – взаимно однозначный}.◄
{f – взаимно однозначный}.◄
Теорема 4.6.Произведение невырожденных линейных операторов – невырожденный линейный оператор.
►Пусть 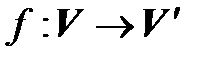 и
и 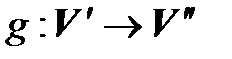 – невырожденные линейные операторы. Тогда
– невырожденные линейные операторы. Тогда
{ 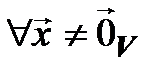 }
}  {
{ 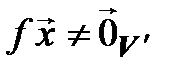 }
}  {
{ 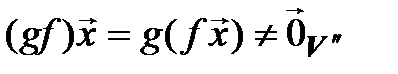 }.
}.
Tаким образом, gf – невырожденный линейный оператор.◄
Вопрос 22
Обратный линейный оператор
Теорема 4.7. Для любого невырожденного линейногооператора 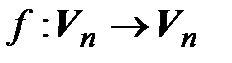 существует единственный обратный оператор
существует единственный обратный оператор 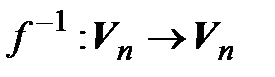 , который также является линейным. При этом, если А – матрица оператора
, который также является линейным. При этом, если А – матрица оператора 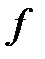 в некотором базисе, то матрица оператора
в некотором базисе, то матрица оператора 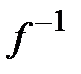 в том же базисе совпадает с матрицей
в том же базисе совпадает с матрицей 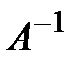 .
.
►Единственность. Пусть некоторый оператор 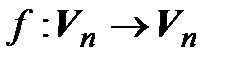 имеет два разных обратных:
имеет два разных обратных: 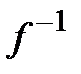 и
и 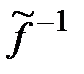 . Тогда
. Тогда
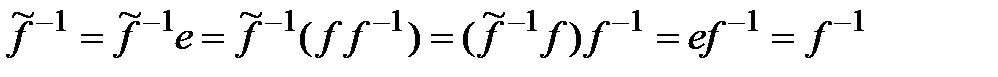
– противоречие.
Существование. Пусть А – матрица оператора 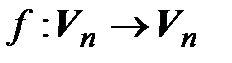 в некотором базисе. Тогда, по теореме 4.4
в некотором базисе. Тогда, по теореме 4.4 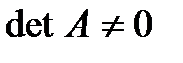 , значит, существует
, значит, существует 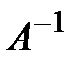 . Обозначим
. Обозначим 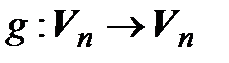 – тот линейный оператор, матрица которого в выбранном базисесовпадаетс
– тот линейный оператор, матрица которого в выбранном базисесовпадаетс 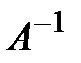 .
.
Так как 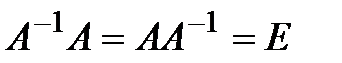 , и так как произведению матриц соответствует произведение операторов, то
, и так как произведению матриц соответствует произведение операторов, то 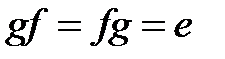 , и, таким образом,
, и, таким образом, 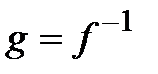 .◄
.◄
Замечание. Можно доказать, что любой взаимно однозначный линейный оператор 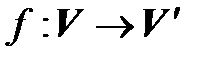 имеет единственный обратный, который тоже является линейным.
имеет единственный обратный, который тоже является линейным.
Вопрос 23
Определение и свойства изоморфизма линейных пространств
Определение.Изоморфизмом линейных пространств называется взаимно однозначный линейный оператор. Если существует изоморфизм 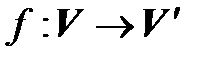 , то линейные пространства
, то линейные пространства 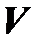 и
и 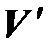 называются изоморфными. Изоморфизм обозначается так:
называются изоморфными. Изоморфизм обозначается так: 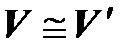 .
.
Так как изоморфизм – взаимно однозначное отображение, то изоморфные объекты содержат одинаковое количество элементов. Кроме того, в силу линейности, действия, производимые над элементами пространства 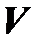 , одновременно производятся и над элементами пространства
, одновременно производятся и над элементами пространства 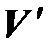 . Поэтому в математике изоморфные объекты не различаются.
. Поэтому в математике изоморфные объекты не различаются.
Свойства изоморфизма
1. 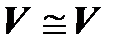 – рефлективность (изоморфизм осуществляет тождественное отображение).
– рефлективность (изоморфизм осуществляет тождественное отображение).
2. 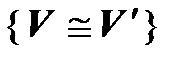

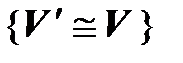 – симметричность (если первый изоморфизм осуществляет с помощью отображения f, то второй – с помощью
– симметричность (если первый изоморфизм осуществляет с помощью отображения f, то второй – с помощью 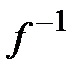 ).
).
3. { 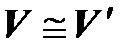 ,
, 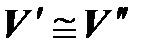 }
} 
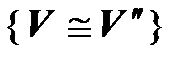 – транзитивность (если первый изоморфизм осуществляется с помощью отображения
– транзитивность (если первый изоморфизм осуществляется с помощью отображения 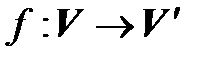 , второй –
, второй – 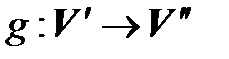 , то третий изоморфизм осуществляется с помощью отображения
, то третий изоморфизм осуществляется с помощью отображения 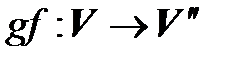 ).
).
Строгого доказательства этих свойств мы не приводим.
Вопрос 24
