Алгоритм решения уравнения в полных дифференциалах 2 страница
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Расширенное понятия числа. Основные понятия и определения комплексного числа.
2. Действия над комплексными числами в алгебраической форме.
3. Геометрическая интерпретация комплексного числа. Тригонометрическая форма записи комплексного числа.
4. Действия над комплексными числами в тригонометрической форме записи.
5. Формула Эйлера. Показательная форма комплексного числа. Действия над комплексными числами в показательной форме.
6. Представление комплексного числа в тригонометрической и показательной формах. Переход комплексного числа из тригонометрической формы в алгебраическую, из показательной в алгебраическую. Обратный переход.
7.
8.
Практическая работа №4
Тема: Решение задач на векторы и координаты.
Цель: Научиться находить с помощью векторов и координат длины отрезков, углы, площади и объемы.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
| Плоскость | Прямая в пространстве | Прямая на плоскости | ||||
| Общие уравнения | α: 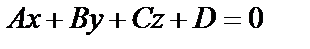 , , 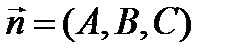 - нормальный вектор плоскости - нормальный вектор плоскости 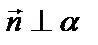 | 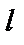 : : 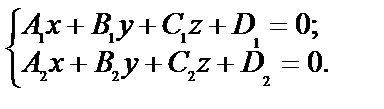 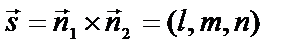 - направляющий вектор. - направляющий вектор. | 1) 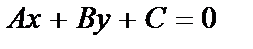 , , 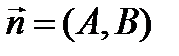 - общее уравнение; - общее уравнение; 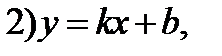 - уравнение с угловым коэффициентом. - уравнение с угловым коэффициентом. 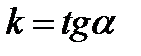 . . | |||
| Способы задания | 1) по точке М 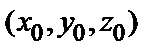 и нормальному вектору и нормальному вектору 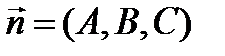 : : 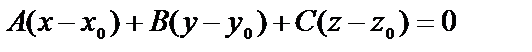 ; 2) по трем точкам: ; 2) по трем точкам: 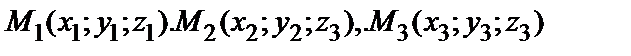 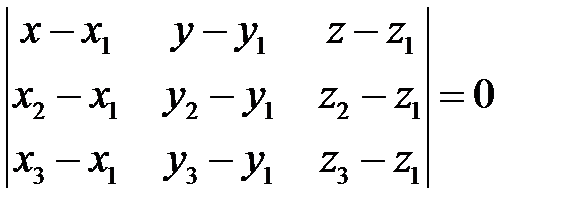 ; 2) в “отрезках” : ; 2) в “отрезках” : 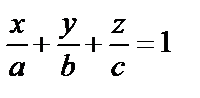 . . | 1)по точке М 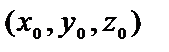 и направ- ляющему вектору и направ- ляющему вектору 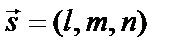 ; ; 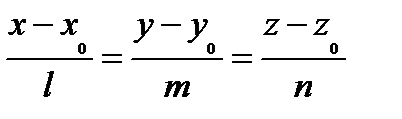 2)по двум точкам: 2)по двум точкам: 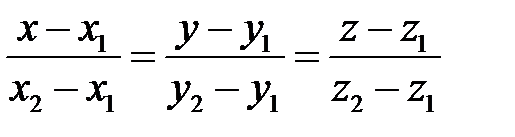 ; 3)параметрические уравнения: ; 3)параметрические уравнения: 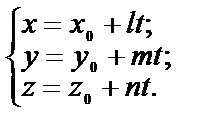 | 1)по точке М 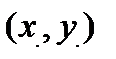 и направляющему вектору и направляющему вектору 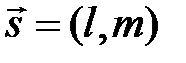 : : 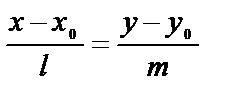 ; 2)по двум точкам: ; 2)по двум точкам: 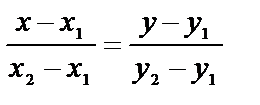 ; 3)в “отрезках” : ; 3)в “отрезках” : 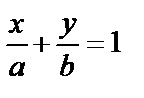 ; 4) параметрические уравнения: ; 4) параметрические уравнения: 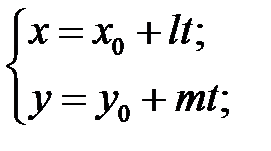 5)по точке M 5)по точке M 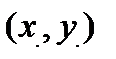 и угловому коэффициенту и угловому коэффициенту 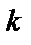 : : 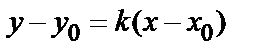 | |||
| приложения | 1)угол между плоскостями α1 и α2: 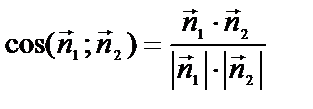 ; 2) ; 2) 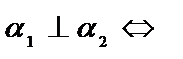 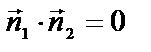 ; 3) ; 3) 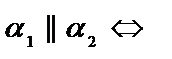 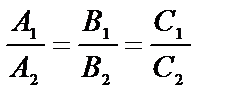 ; 4)расстояние от точки М ; 4)расстояние от точки М 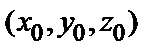 до плоскости: до плоскости: 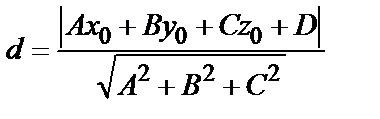 . . | 1)угол между прямыми 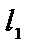 и и 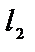 : : 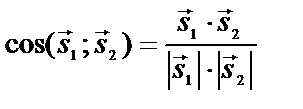 ; 2) ; 2) 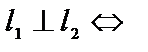 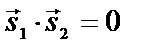 ; 3) ; 3) 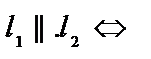 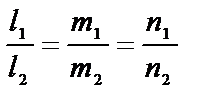 ; 4)расстояние от точки М ; 4)расстояние от точки М 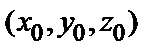 до прямой: до прямой: 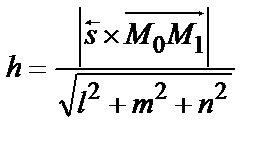 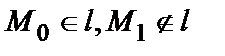 . . | 1) угол между прямыми 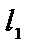 и и 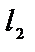 : : 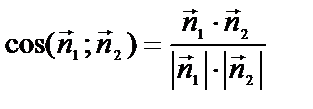 или или 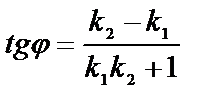 ; 2) ; 2) 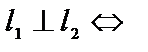 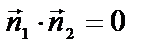 , , 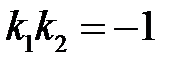 3) 3) 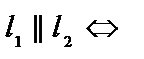 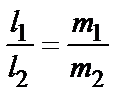 , , 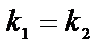 ; 4) расстояние от точки до прямой: ; 4) расстояние от точки до прямой: 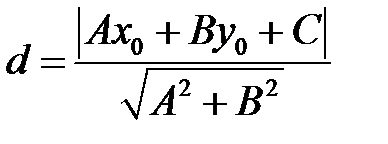 . . | |||
Взаимное расположение прямой и плоскости, 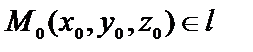 : : 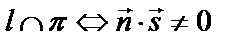 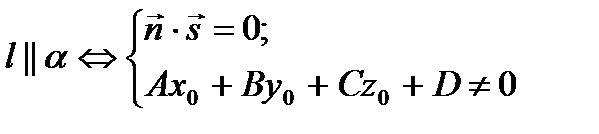 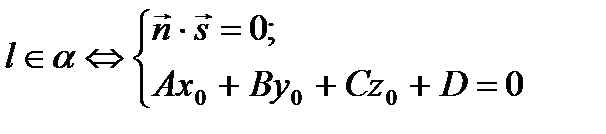 | Условие пересечения двух прямых в пространстве: 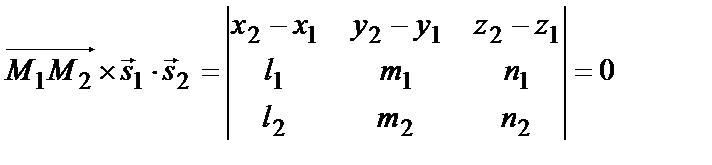 | Угол между прямой и плоскостью: 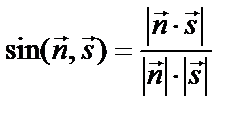 | ||||
 ВАРИАНТЫ
ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
1. Прямая на плоскости.
Даны вершины треугольника 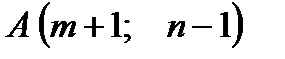 ,
, 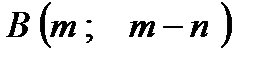 ,
, 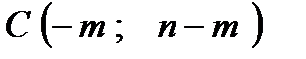 . Найти:
. Найти:
1) координаты точки пересечения медиан;
2) длину и уравнение высоты, опущенной из вершины А;
3) площадь треугольника;
2. Прямая и плоскость в пространстве.
Дана треугольная пирамида с вершинами в точках 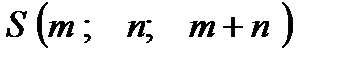 ,
, 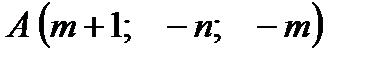 ,
, 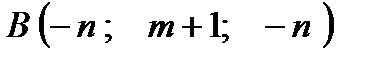 ,
, 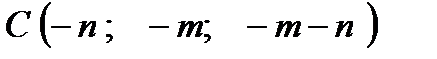 . Найти:
. Найти:
1) уравнение плоскости, проходящей через точки А, В и С;
2) величину угла между ребром SC и гранью АВС;
3) площадь грани АВС;
4) объем пирамиды SАВС.
5) уравнение высоты, опущенной из вершины S на грань АВС, и ее длину;
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Декартова система координат. Работа с отрезками через координаты.
2. Вектора. Произведение векторов. Применение.
3. Уравнения линии на плоскости.
4. Угол между прямыми. Условия параллельности и перпендикулярности двух прямых.
5. Уравнение прямой линии и плоскости в пространстве.
6.
Практическая работа №5
Тема: Построение кривых и поверхностей второго порядка.
Цель: Научиться определять тип кривых и поверхностей второго порядка и строить их чертежи.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Кривая второго порядка – геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида
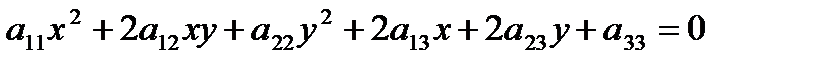 ,
,
в котором по крайней мере один из коэффициентов 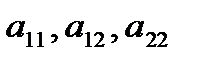 отличен от нуля.
отличен от нуля.
Инварианты.
Вид кривой зависит от трёх инвариантов относительно поворота и сдвига системы координат:
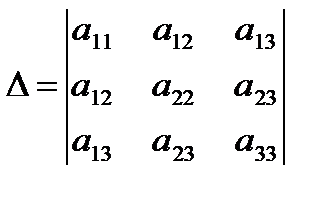
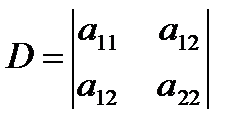
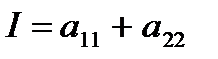
Характеристическая квадратичная форма и характеристическое уравнение.
Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой
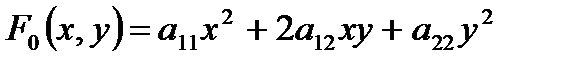
Так, например, невырожденная кривая (Δ≠0) оказывается вещественным эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости от того, будет ли 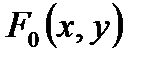 положительно определённой, отрицательно определённой, неопределённой или полуопределённой квадратичной формой, что устанавливается по корням характеристического уравнения:
положительно определённой, отрицательно определённой, неопределённой или полуопределённой квадратичной формой, что устанавливается по корням характеристического уравнения:
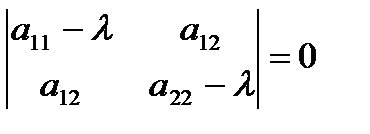 или
или 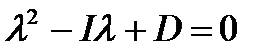 .
.
Корни этого уравнения являются вещественными числами.
Классификация кривых второго порядка.
| Вид кривой | Каноническое уравнение | Инварианты |
| Невырожденные кривые (Δ≠0) | ||
| Эллипс | 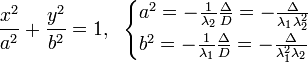 | 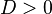 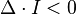 |
| Гипербола | 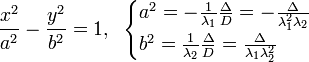 | 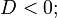 |
| Парабола | 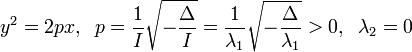 | 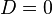 |
| Вырожденные кривые (Δ=0) | ||
| Две мнимые пересекающиеся прямые | 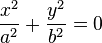 | 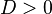 |
| Две пересекающиеся прямые | 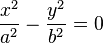 | 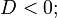 |
| Две параллельные прямые | 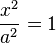 | 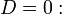 |
Главные оси и вершины кривой второго порядка.
Главной осью кривой второго порядка называется её диаметр, перпендикулярный к сопряжённым к ним хордам. Этот диаметр является осью симметрии кривой. Каждая центральная кривая либо имеет две взаимно перпендикулярные оси, либо все диаметры являются главными осями. В последнем случае кривая является окружностью. Нецентральные кривые имеют лишь одну главную ось. Точки пересечения главной оси с самой кривой называются её вершинами.
Угол между положительным направлением оси Ox и каждым из двух главных направлений определяется формулой 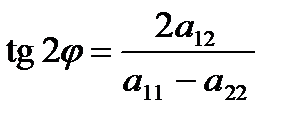 .
.
Центр кривой второго порядка
Координаты центра 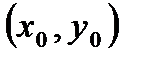 определяются системой уравнений:
определяются системой уравнений:
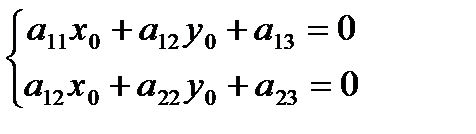
Решая эту систему относительно x0 и y0 получим (D ≠ 0):
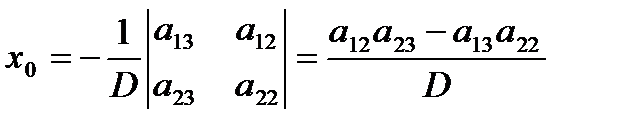
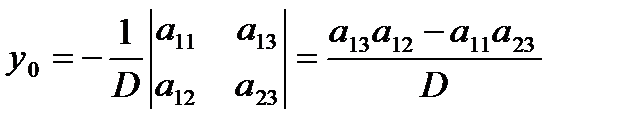
Если кривая центральная, то перенос начала координат в её центр приводит уравнение к виду
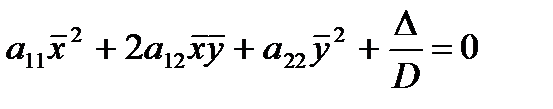 ,
, 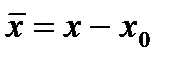 ,
, 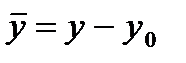 , где x̅, y̅ — координаты относительно новой системы.
, где x̅, y̅ — координаты относительно новой системы.
Эллипс
 Определение. Эллипс – это множество точек (x, y), сумма расстояний каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2а.
Определение. Эллипс – это множество точек (x, y), сумма расстояний каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2а.
Каноническое уравнение 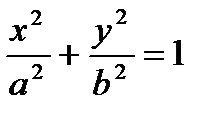 .
.
Принятые названия:
· 2a – большая ось эллипса, на ней расположены фокусы;
· 2b – малая ось эллипса, b<a;
· F1(c,0), F2(-c,0) – фокусы эллипса;
· 2с – расстояние между фокусами, c < a, 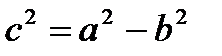 ;
;
· 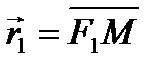 ,
, 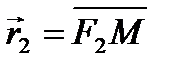 – фокальные радиус-векторы (по определению
– фокальные радиус-векторы (по определению 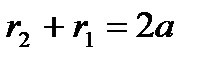 );
);
· 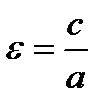 называется эксцентриситетом,
называется эксцентриситетом, 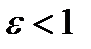 ;
;
· 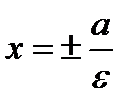 называется директрисами эллипса (отношение расстояний от любой точки эллипса до фокуса и соответствующей директрисы есть величина постоянная, равна ε).
называется директрисами эллипса (отношение расстояний от любой точки эллипса до фокуса и соответствующей директрисы есть величина постоянная, равна ε).
Гипербола
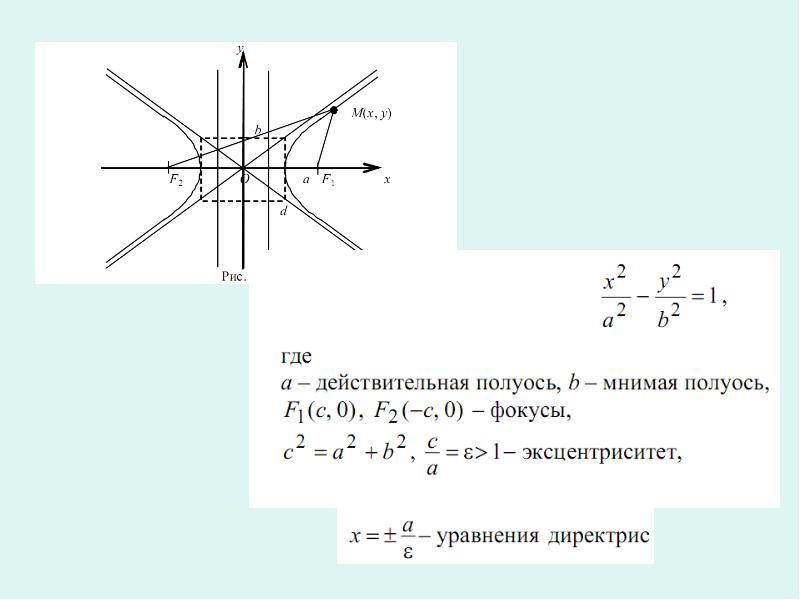 Определение. Гипербола – это множество точек (x, y), разность расстояний каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2а.
Определение. Гипербола – это множество точек (x, y), разность расстояний каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2а.
Каноническое уравнение 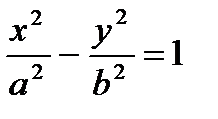 .
.
Принятые названия:
· 2a – большая ось гиперболы, на ней расположены фокусы;
· 2b – малая ось гиперболы, b<a;
· F1(c,0), F2(-c,0) – фокусы гиперболы;
· 2с – расстояние между фокусами, 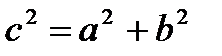 ;
;
· 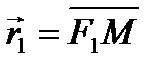 ,
, 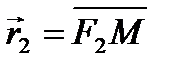 – фокальные радиус-векторы (по определению
– фокальные радиус-векторы (по определению 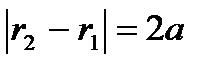 );
);
· 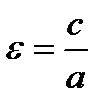 называется эксцентриситетом,
называется эксцентриситетом, 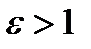 ;
;
· 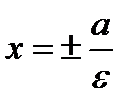 называется директрисами гиперболы (отношение расстояний от любой точки гиперболы до фокуса и соответствующей директрисы есть величина постоянная, равна ε).
называется директрисами гиперболы (отношение расстояний от любой точки гиперболы до фокуса и соответствующей директрисы есть величина постоянная, равна ε).
Парабола
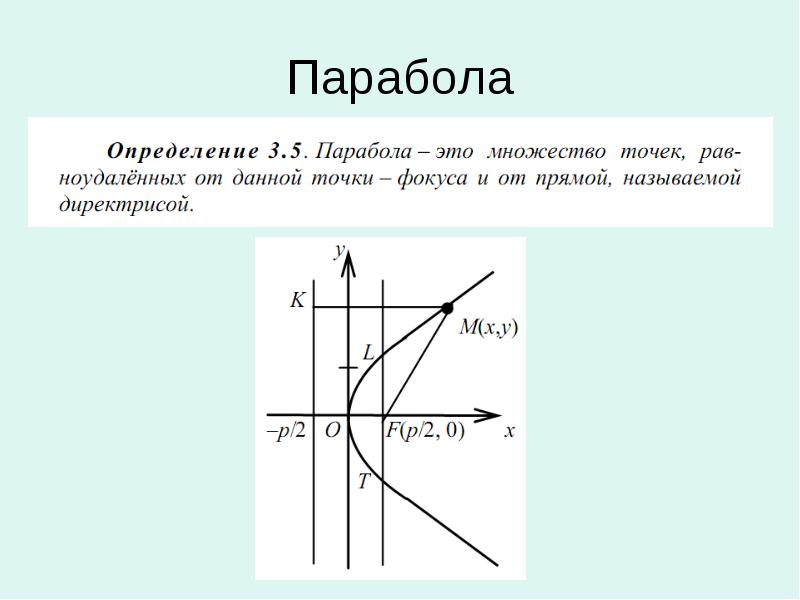 Определение. Парабола – это множество точек (x, y), равноудаленных от данной точки, называемой фокусом, и от прямой, называемой директрисой.
Определение. Парабола – это множество точек (x, y), равноудаленных от данной точки, называемой фокусом, и от прямой, называемой директрисой.
Каноническое уравнение 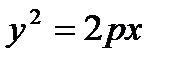 .
.
Принятые названия:
· OX –ось симметрии параболы, на ней расположен фокус;
· F(p/2,0) – фокус параболы;
· 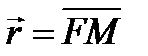 – фокальный радиус-вектор (по определению
– фокальный радиус-вектор (по определению 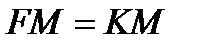 );
);
· 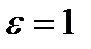 называется эксцентриситетом;
называется эксцентриситетом;
· 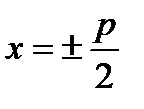 называется директрисами параболы (отношение расстояний от любой точки параболы до фокуса и директрисы есть величина постоянная, равна ε=1).
называется директрисами параболы (отношение расстояний от любой точки параболы до фокуса и директрисы есть величина постоянная, равна ε=1).

ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
1. Определить тип кривой второго порядка и построить ее чертеж: 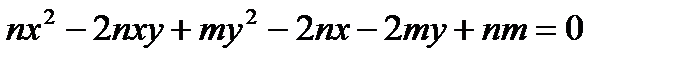 .
.
2. Определить тип поверхности второго порядка и построить ее чертеж:
a) 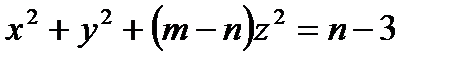 ;
;
b) 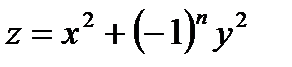 .
.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Канонические уравнения кривых и поверхностей второго порядка.
2. Чертежи кривых и поверхностей второго порядка.
3. Центр, полуоси, фокусы, эксцентриситет, директрисы.
4. Классификация кривых второго порядка с помощью инвариант.
Практическая работа №6
Тема: Вычисление пределов.
Цель: Научиться вычислять пределы функций.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Понятие предела последовательности. Предел функции в точке. Односторонние пределы в точке. Свойства  пределов. Замечательные пределы. Непрерывность функции. Точки разрыва и их классификация.
пределов. Замечательные пределы. Непрерывность функции. Точки разрыва и их классификация.
Числовой последовательностью называется упорядоченная совокупность чисел 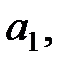
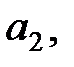 …,
…, 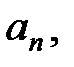 каждое из которых определяется по заданному правилу соответствия
каждое из которых определяется по заданному правилу соответствия 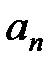 =f(n), где переменная n – натуральное число.
=f(n), где переменная n – натуральное число.
Число A называется пределом числовой последовательности 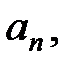 , если все члены последовательности приближаются к этому числу при неограниченном возрастании номера n:
, если все члены последовательности приближаются к этому числу при неограниченном возрастании номера n: 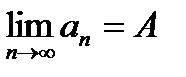 .
.
Предел A функции y=f(x) в точке a записывается в виде 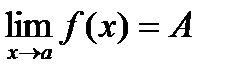 и означает, что для всех значений x, достаточно близких к числу a (и отличных от него), соответствующие значения функции y=f(x) оказываются сколь угодно близкими к числу A.
и означает, что для всех значений x, достаточно близких к числу a (и отличных от него), соответствующие значения функции y=f(x) оказываются сколь угодно близкими к числу A.
Если x<a, 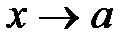 , то употребляют запись
, то употребляют запись 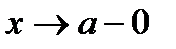 ; если x>a,
; если x>a, 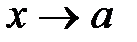 –
– 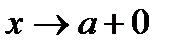 . Числа
. Числа 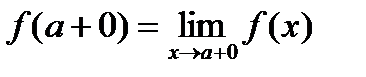 и
и 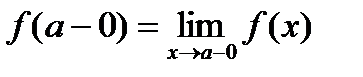 называются соответственно левым и правым пределом функции f(x) в точке a. Для существования предела функции f(x) при
называются соответственно левым и правым пределом функции f(x) в точке a. Для существования предела функции f(x) при 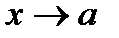 необходимо и достаточно, чтобы f(a+0)=f(a–0).
необходимо и достаточно, чтобы f(a+0)=f(a–0).
Основные теоремы о пределах: 1) Предел суммы конечного числа функций, имеющих пределы, равен сумме пределов этих функций. 2) Предел произведения конечного числа функций, имеющих пределы, равен произведению пределов функций. 3) Предел частного от деления двух функций, имеющих пределы, равен частному от деления пределов этих функций, если предел знаменателя не равен нулю.
Замечательные пределы: 1) 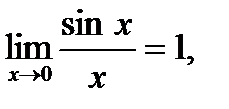 ; 2)
; 2) 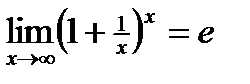 .
.
Функция f(x) называется непрерывной в точке a, если она определена в окрестности точки a; существует предел функции f(x) в точке a; этот предел равен значению функции в точке a, т.е. 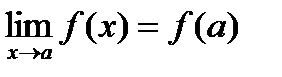 , или f(a–0)=f(a+0)=f(a).
, или f(a–0)=f(a+0)=f(a).
Точка a, принадлежащая области определения функции или являющаяся граничной для этой области, называется точкой разрыва, если в этой точке нарушается условие непрерывности функции.
Если существуют конечные пределы f(a–0) и f(a+0), причем не все три числа f(a–0), f(a+0), f(a) равны между собой, то a называется точкой разрыва I рода. Точки разрыва I рода подразделяются в свою очередь, на точки устранимого разрыва (когда f(a–0)=f(a+0) 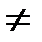 f(a)) и на точки скачка (когда f(a–0)
f(a)) и на точки скачка (когда f(a–0) 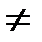 f(a+0)). Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода.
f(a+0)). Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода.
ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
Найти пределы функций:
1) 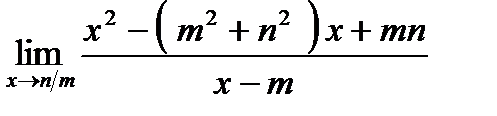 ;
;
2) 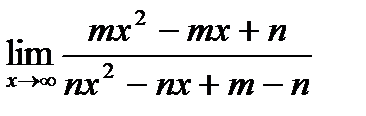 ;
;
3) 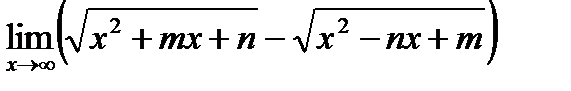 ;
;
4) 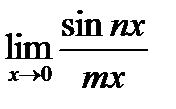 ;
;
5) 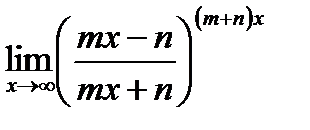 .
.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Предел функции. Свойства.
2. Непрерывность функции. Точки разрыва.
3.
Практическая работа №7
Тема: Нахождение производной функции.
Цель: Научиться вычислять производные функций.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.
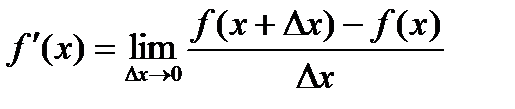
Основные правила дифференцирования.
Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.
1) (C×u)¢ = C×(u)¢
2) (u ± v)¢ = u¢ ± v¢
3) (u×v)¢ = u×v¢ + u¢×v
4) 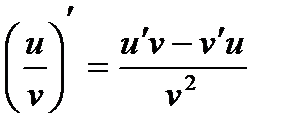 , если v ¹ 0
, если v ¹ 0
