Довірчий інтервал для лінії регресії

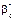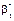Ураховуючи те, що і є випадковими величинами, то і лінійна функція регресії 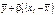буде випадковою. Позначимо через 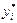значення ознаки Y, обчислимо за формулою

.

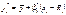Тоді

.

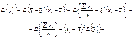
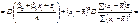
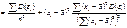
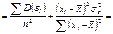
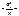
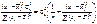Звідси дістали:

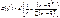або

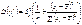.Випадкова величина

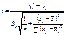
має t-розподіл із 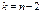ступенями свободи. Ураховуючи можна побудувати довірчий інтервал для лінійної парної функції регресії із заданою надійністю γ, а саме:

.

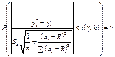випливає

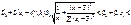
Множина регресії ,множинний коєфіцієнт кореляції та його властивості .

На практиці здебільшого залежна змінна 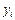пов’язана з впливом не одного, а кількох аргументів.
У цьому разі регресію називають множинною. При цьому якщо аргументи в функції регресії в першій степені, то множинна регресія називається лінійною, у противному разі — множинною нелінійною регресією.

Довірчий інтервал для множинної лінійної регресії

Матриця Х містить m лінійно незалежних векторів-стовпців, а це означає, що ранг її дорівнюватиме m і визначник 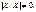Отже, матриця 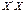має обернену.

Дисперсії статистичних оцінок 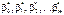визначають з допомогою кореляційної матриці для вектора

Коефіцієнт множинної регресіїТісноту між ознаками Y та X, де 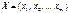, вимірюють з допомогою коефіцієнта множинної кореляції R, що є узагальненням парного коефіцієнта кореляції r_ij і обчислюється за формулою

.

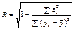Чим ближче значення R до ±1, тим краще вибрано функцію регресії

Нормування коефіцієнтів регресії

Множинна лінійна регресія дає змогу порівняти вплив на досліджуваний процес різних чинників. У загальному випадку змінні 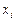репрезентують чинники, що мають різні одиниці виміру (кілограми, гривні, метри тощо). Отже, для того щоб порівняти і з’ясувати відносну вагомість кожного з чинників, використовують так звані нормовані коефіцієнти регресії, які визначають за формулою

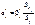
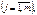
де 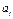— коефіцієнт регресії після нормування; 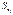— виправлене середнє квадратичне відхилення змінної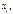 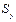— виправлене середнє квадратичне відхилення ознаки Y.

Нелінійна регресія.

Якщо в рівняння множинної регресії змінні 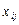входять як 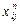, то регресія називається нелінійною.

У загальному випадку нелінійна регресія записується в такому вигляді:

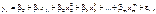
де параметри 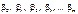є сталими невідомими величинами, які підлягають статистичним оцінкам, а 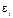— випадкова величина, яка має нормальний закон розподілу з числовими характеристиками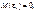 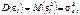і при цьому випадкові величини 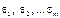між собою не корельовані. Реалізуючи вибірку обсягом n, згідно з (563), дістанемо систему нелінійних рівнянь виду:

2.Класифікація подій ,класичне означення ймовірності випадкової події ,статистичне означення ймовірності;елементи комбінаторики ;аксіоми теорії ймовірностей та їх наслідки. 3 Залежні й незалежні випадкові події, формули додавання ймовірностей. 4 Умовна ймовірність та її властивості. 5 Формули множення ймовірностей для залежних та незалежних випадкових подій. 6 Формула повної ймовірності та формула Байеса. 7 Означення повторних незалежних випробувань. 8 Формула Бернуллі для обчислення ймовірності і наймовірнішого числа. 9 Локальна та інтегральна теореми Мавра-Лапласа. 10 Формула Пуассона малоймовірних випадкових подій. 11 Означення випадкової величини. 12.Випадковою називається величина, яка може набувати різних числових значень. 13. Функція розподілу 14,Математичним сподіванням, 15. Сукупність випадкових величин 16.Сукупність випадкових величин 17. Функція розподілу 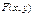системи двох випадкових величин визначає ймовірність спільного настання двох подій: 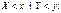19.Сукупність випадкових величин 20.Нехай закон дискретной випадкової величини Х задано таблицею: 23. Означення дискретної випадкової величини 24. Біноміальний закон розподілу 25. Числові характеристики розподілу Біноміального закону розподілу: 26. Рівномірний закон розподілу 27. Нормальний закон розподілу 28. Логарифмічний нормальний закон розподілу 29. Показниковий закон розподілу 30. Розподіл 31. Розподіл Стьюдента 32. Розподіл Фішера 33. . Закон великих чисел, центральна гранична теорема. Нерівності Чебишова. 34) Нерівності Чебишова та її значення 35) Теорема Чебишова 36) Теорема Бернулі 37) Центральна гранична теорема. 38) Випадковим процесом 39) Потоком подій називається послідовність подій, які відбуваються одна за одною у випадкові моменти часу. 40) Формула Пуассона для найпростішого потоку 41) Марковські випадкові ланцюги 42). Системи для розвязування однотипних задач називаються системами масового обслуговування -(СМО) 44) Генеральною сукупністю 45) Дискретний статистичнй розподіл 46) Полігон частот і відносних частот 47) Числові характеристики 48) Визначення статистичної оцінки 49) Точкові та інтервальні статистичні оцінки 51) Нульова та альтернативна статистичні гіпотези 53) Статистичний критерій 54) Критична область 55) Перевірка правельності нульової гіпотези про нормальний закон розподілу ознаки генеральної сукупності 57) Критерій узгодженості Пірсона 58) Дисперсійний аналіз 59) Однофакторний аналіз 60) Таблиця результатів спостережень 61) Загальна дисперсія ,міжгрупова та внутрішнлогрупова дисперсія 62) Загальний метод перевірки впливу фактора на ознаку способом порівняння дисперсій 63) Двофакторний дисперсійний аналіз. 64) Функціональна ,статистична і кореляційна залежності. 65) Рівняння лінійної регресії . 66) Вибірковий коефіцієнт кореляції 67) Довірчий інтервал для лінії регресії 68) Множина регресії ,множинний коєфіцієнт кореляції та його властивості . 69) Нелінійна регресія