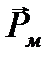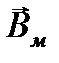Примеры решения задач по электромагнетизму
| a |
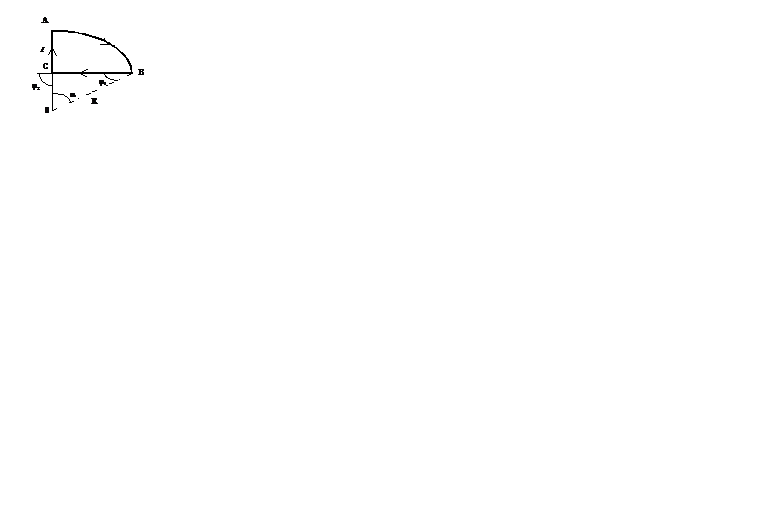 Пример 1. По контуру, изображённому на рисунке, идёт ток силой I = 10 А. Определить магнитную индукцию в точке О, если радиус дуги
Пример 1. По контуру, изображённому на рисунке, идёт ток силой I = 10 А. Определить магнитную индукцию в точке О, если радиус дуги 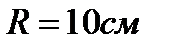 ,
, 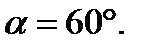
Решение
По принципу суперпозиции полей
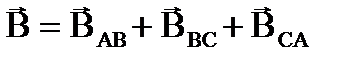 .
.
Магнитную индукцию, создаваемую дугой AB, найдём путём интегрирования:
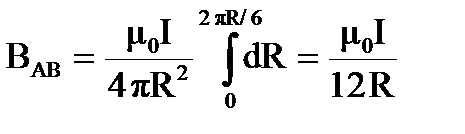 .
.
Для нахождения магнитной индукции, создаваемой проводником BC, воспользуемся формулой
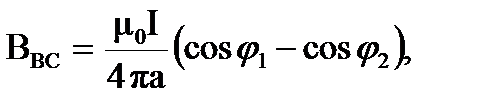
где 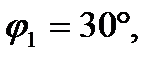
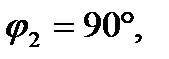
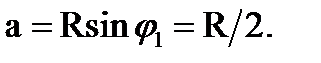
С учётом данных значений 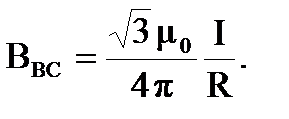
Магнитная индукция ВСА, создаваемая проводником СА в точке О, равна нулю, т. к. для любого элемента 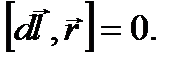 Поскольку вектор
Поскольку вектор 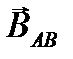 направлен от наблюдателя, а вектор
направлен от наблюдателя, а вектор 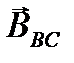 – к наблюдателю, то результирующая индукция равна
– к наблюдателю, то результирующая индукция равна
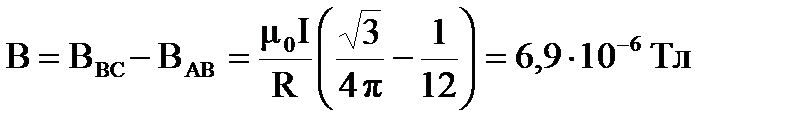 .
.
Пример 2. Рядом с длинным прямым проводом MN, по которому течёт ток силой I1, расположена квадратная рамка со стороной b, обтекаемая током силой I2. Рамка лежит в одной плоскости с проводником MN, так что её сторона, ближайшая к проводу, находится от него на расстоянии a. Определить магнитную силу, действующую на рамку, а также работу этой силы при удалении рамки из магнитного поля.
Решение
Рамка с током находится в неоднородном магнитном поле, создаваемым бесконечно длинным проводником MN:
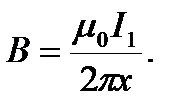
Каждая сторона рамки будет испытывать действие сил Ампера, направление которых показано на рисунке. Так как стороны АВ и D C расположены одинаково относительно провода MN, действующие на них силы 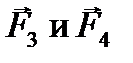 численно равны и равнодействующая всех сил, приложенных к рамке, равна F=F1–F2 ,
численно равны и равнодействующая всех сил, приложенных к рамке, равна F=F1–F2 ,
|
где 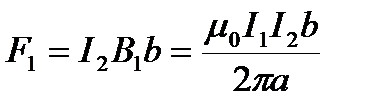 , a
, a
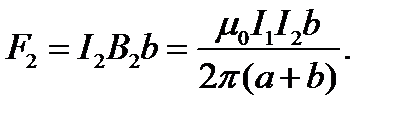
Окончательно
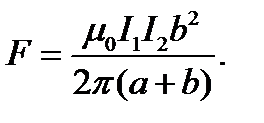
Работа по удалению рамки из магнитного поля равна
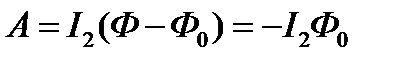 .
.
Для нахождения магнитного потока через рамку в неоднородном магнитном поле разделим её на узкие полосы шириной dx, в пределах которых магнитную индукцию можно считать постоянной. Элементарный магнитный поток через полоску, находящуюся на расстоянии x от прямого тока, равен 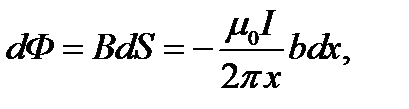 где знак минус обусловлен тем, что Bn =-B.
где знак минус обусловлен тем, что Bn =-B.
После интегрирования по x найдём:
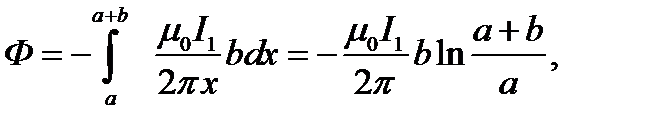 .
.
Окончательно 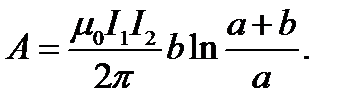
Пример 3.Провод в виде тонкого полукольца радиусом R=10 см находится в однородном магнитном поле (B = 50 мТл). По проводу течёт ток I = 10 А. Найти силу F, действующую на провод если плоскость полукольца перпендикулярна линиям магнитной индукции, а подводящие провода находятся вне поля.
Решение
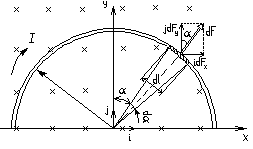
Расположим провод в плоскости чертежа перпендикулярно линиям магнитной индукции и выделим на нём малый элемент dl с током. На этот элемент тока Idl будет действовать по закону Ампера сила 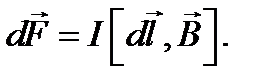 Направление этой силы можно определить по правилу векторного произведения или по правилу левой руки.
Направление этой силы можно определить по правилу векторного произведения или по правилу левой руки.
Используя симметрию, выберем координатные оси так, как это изображено на рисунке. Силу dF представим в виде
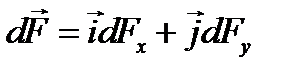 ,
,
где i и j – единичные векторы (орты); dFx и dFy – проекции вектора dF на координатные оси Ox и Oy.
Силу F, действующую на весь провод, найдём интегрированием:
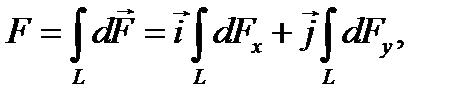
где символ L указывает на то, что интегрирование ведётся по всей длине провода L. Из соображений симметрии первый интеграл равен нулю 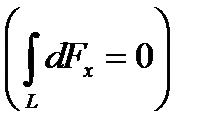 . Тогда
. Тогда
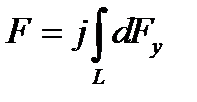 . (1)
. (1)
Из рисунка следует, что dFy = dFcosα, где dF – модуль вектора 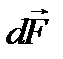 (
( 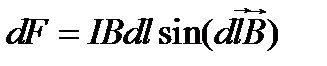 ). Так как вектор
). Так как вектор 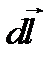 перпендикулярен вектору
перпендикулярен вектору 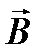 (
( 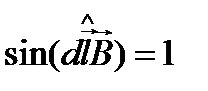 ), то
), то 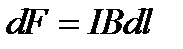 . Выразив длину дуги dl через радиус R и угол α, получим
. Выразив длину дуги dl через радиус R и угол α, получим
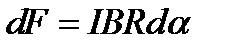 .
.
Тогда
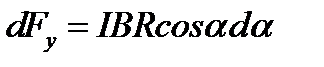 .
.
Введём 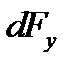 под интеграл соотношения (1) и проинтегрируем в пределах от –π/2 до +π/2 (как это следует из рисунка):
под интеграл соотношения (1) и проинтегрируем в пределах от –π/2 до +π/2 (как это следует из рисунка):
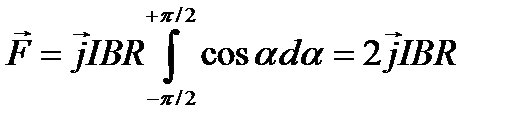 .
.
Из полученного выражения видно, что сила 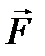 сонаправлена с положительным направлением оси Oy (единичным вектором
сонаправлена с положительным направлением оси Oy (единичным вектором 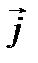 ). Найдём модуль силы
). Найдём модуль силы 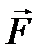 :
:
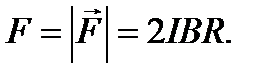
Убедимся в том, что правая часть этого равенства даёт единицу силы (Н):
[I][B][R]=1А·1Тл·1м = 1А·1Н·1м·1м/(1А·(1м)2)=1Н.
Произведём вычисления: F = 2·10·50·10-3·0,1Н = 0,1Н.
Пример 4. В центре длинного соленоида, имеющего n=5×103 витков на метр, помещена рамка, состоящая из N=50 витков провода площадью S = 4 см2. Рамка может вращаться вокруг оси ОО, перпендикулярной оси соленоида. При пропускании тока по рамке и соленоиду, соединённых последовательно, рамка повернулась на угол j = 60°. Oпреде- лить силу тока, если жёсткость пружины, удерживающей рамку в положении равновесия, равна k = 6×10–5Н·м / рад.
Решение
При появлении тока рамка установится в таком положе- нии, когда момент сил магнитного поля М уравновесится моментом упругих сил пружины: M=Mупр.
По определению 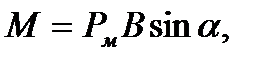 где
где 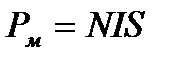 – магнитный момент,
– магнитный момент, 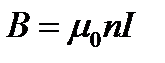 – индукция поля соленоида.
– индукция поля соленоида.
|
С учётом этих выражений имеем:
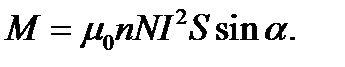
Заметим, что вначале, когда тока нет,
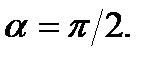 Согласно закону Гука
Согласно закону Гука
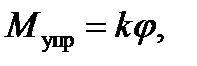
где 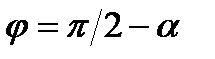 и, следовательно,
и, следовательно, 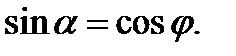
Таким образом, 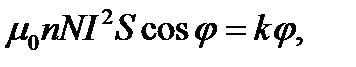 откуда
откуда
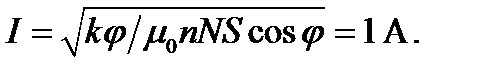
Пример 5. Электрон, влетев в однородное магнитное поле с индукцией 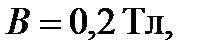 стал двигаться по окружности радиуса
стал двигаться по окружности радиуса 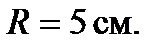 Определить магнитный момент
Определить магнитный момент 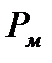 эквива- лентного кругового тока.
эквива- лентного кругового тока.
Решение
|
| -e |
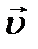 |
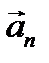 |
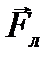 |
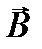 |
| R |
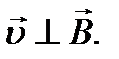 В этом случае сила Лоренца
В этом случае сила Лоренца 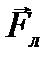 сообщит электрону нормальное ускорение
сообщит электрону нормальное ускорение 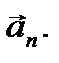
Согласно второму закону Ньютона 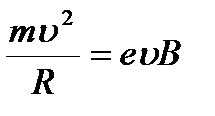
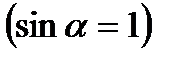 . Отсюда находим скорость электрона
. Отсюда находим скорость электрона 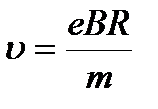 и период его обращения
и период его обращения 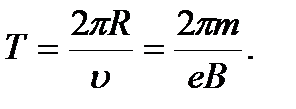
Движение электрона по окружности эквивалентно круговому току
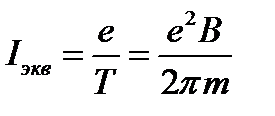 .
.
Зная 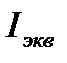 , найдем магнитный момент эквивалентного тока, который выражается соотношением
, найдем магнитный момент эквивалентного тока, который выражается соотношением
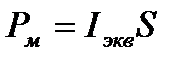 ,
,
где S=πR2 – площадь, ограниченная окружностью, описываемой электроном.
Подставим значения 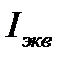 и S в формулу магнитного момента, окончательно получим
и S в формулу магнитного момента, окончательно получим 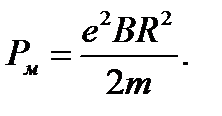
Убедимся в том, что правая часть равенства даст единицу измерения магнитного момента (Ам2):
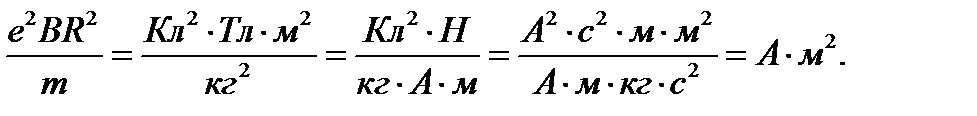
Произведем вычисление:
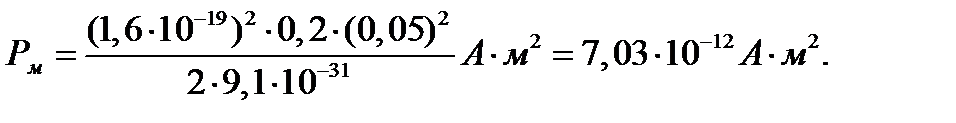
Пример 6. Электрон движется в однородном магнитном поле с индукцией В = 10мТл по винтовой линии, радиус которой равен 1 см и шаг h = 6 см. Определить период Т обращения электрона и его скорость υ.
Решение
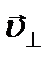 |
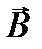 |
| a |
| R |
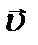 |
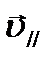 |
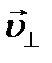 |
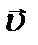 электрона на две составляю- щие: параллельную вектору
электрона на две составляю- щие: параллельную вектору 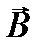 -
- 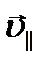 и перпендикулярную ему
и перпендикулярную ему 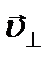 .
. Скорость 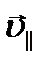 в магнитном поле не изменяется и обеспе- чивает перемещение электрона вдоль силовой линии. Скорость
в магнитном поле не изменяется и обеспе- чивает перемещение электрона вдоль силовой линии. Скорость 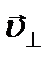 в результате действия силы Лоренца будет изменяться только по направлению, обеспечивая движение по окружно- сти. Таким образом, электрон будет участвовать одновременно в двух движениях: равномерном перемещении его со скоростью
в результате действия силы Лоренца будет изменяться только по направлению, обеспечивая движение по окружно- сти. Таким образом, электрон будет участвовать одновременно в двух движениях: равномерном перемещении его со скоростью 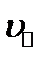 и вращательном со скоростью
и вращательном со скоростью 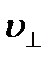 .
.
Согласно второму закону Ньютона
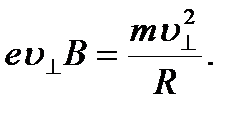
Перпендикулярная составляющая скорости будет равна
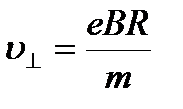 .
.
Период обращения электрона связан именно с этой составляю- щей скоростью соотношением
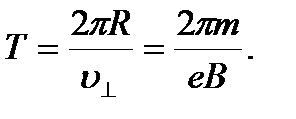
Проверим размерность полученного выражения и произведем вычисление:
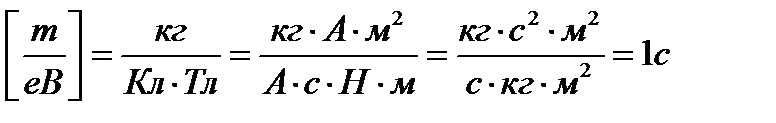
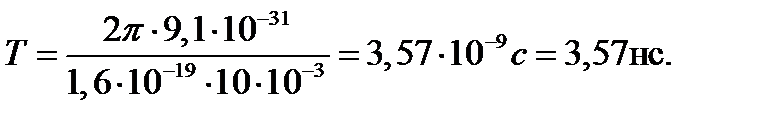
Модуль скорости υ, как видно из рисунка, можно выразить через 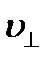 и
и 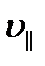 :
:
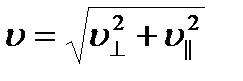
Параллельную составляющую скорости 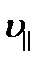 найдем из следующих соображений. За время, равное периоду обращения Т, электрон пройдет вдоль силовой лини расстояние h, т.е.
найдем из следующих соображений. За время, равное периоду обращения Т, электрон пройдет вдоль силовой лини расстояние h, т.е. 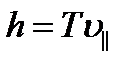 , откуда
, откуда
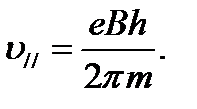
Таким образом, модуль скорости электрона
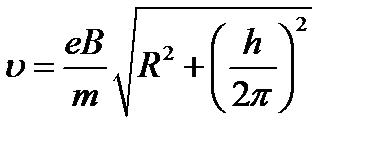
Произведем вычисления:
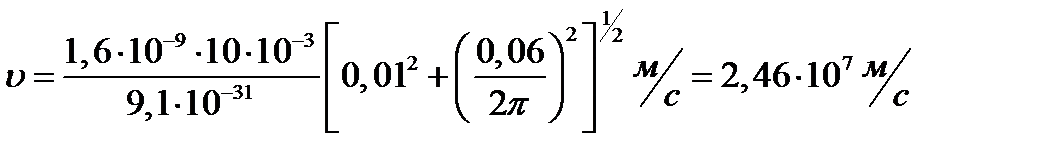 .
.
Пример 7.В одной плоскости с бесконечно длинным прямым проводом, по которому течёт ток I = 50А, расположена прямоугольная рамка так, что две большие стороны её длиной l = 65см параллельны проводу, а расстояние от провода до ближайшей из этих сторон равно её ширине. Каков магнитный поток Ф, пронизывающий рамку?
Решение
Магнитный поток Ф через поверхность площадью S определяется выражением
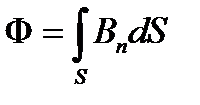 .
.
В нашем случае вектор магнитной индукции 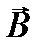 перпендикулярен плоскости рамки. Поэтому для всех точек рамки Bn=B. Магнитная индукция B, создаваемая бесконечно длинным прямым проводником с током, определяется формулой
перпендикулярен плоскости рамки. Поэтому для всех точек рамки Bn=B. Магнитная индукция B, создаваемая бесконечно длинным прямым проводником с током, определяется формулой
| I |
| l |
| x |
| dx |
| a |
| a |
| B S * |
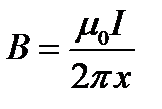 ,
,
| dS=ldxx |
Для вычисления магнит- ного потока заметим, что так как В зависит от х и элементарный поток Ф будет также зависеть от х, то
dФ=В(х)dS.
Разобьём площадь рамки на узкие элементарные площадки длиной l, шириной dx и площадью dS=ldx (см. рис.). В пределах этой площадки магнитную индукцию можно считать постоянной, так как все части площадки равноудалены (на расстояние x) от провода. С учётом сделанных замечаний элементарный магнитный поток можно записать в виде
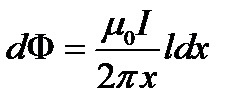 .
.
Проинтегрировав полученное выражение в пределах от x1= a до x2 = 2a, найдём
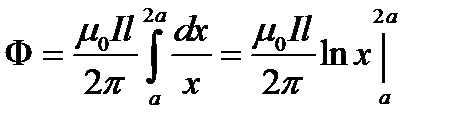 .
.
Подставив пределы, получим
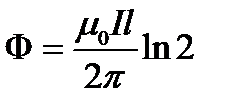 .
.
Убедимся в том, что правая часть полученного равенства дает единицу магнитного потока (Вб):
[μ0][I][l] = 1Гн/м·1А·1м = 1 Вб.
Произведя вычисления, найдём Ф = 4,5 мкВб.
Пример 8.Плоский квадратный контур со стороной а = 10 см, по которому течет ток I = 100А, свободно устано- вился в однородном магнитном поле с индукцией В = 1 Тл. Определить работу А, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон на угол 90˚.
Решение
|
|
| a |
| a |
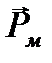 |
| I |
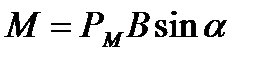 ,
,
где 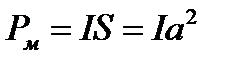 – магнитный момент контура; α – угол между векторами
– магнитный момент контура; α – угол между векторами 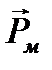 (направлен по направлению положи- тельной нормали к контуру) и
(направлен по направлению положи- тельной нормали к контуру) и 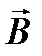 .
.
По условию задачи в начальном положении контур свободно установился в магнитном поле, т.е. М=0, а значит векторы 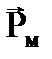 и
и 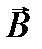 сонаправлены (α=0). Если внешние силы выведут контур из положения равновесия, то возникший момент сил будет стремиться возвратить контур в исходное положение. В силу зависимости М от угля поворота α, для подсчета работы внешних сил воспользуемся методом интегрирования. Элементарная работа равна
сонаправлены (α=0). Если внешние силы выведут контур из положения равновесия, то возникший момент сил будет стремиться возвратить контур в исходное положение. В силу зависимости М от угля поворота α, для подсчета работы внешних сил воспользуемся методом интегрирования. Элементарная работа равна
dA= Mdα = IBa2sin α dα.
Взяв интеграл от этого выражения, найдем работу при повороте контура на конечный угол 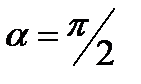 :
:
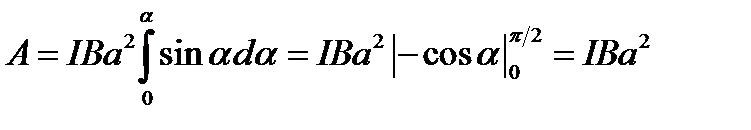 . (1)
. (1)
Производя расчет в единицах СИ, получим
А = 100·1·0,12 Дж =1 Дж.
Задачу можно решить и другими способами:
1) Работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, пронизывающего контур:
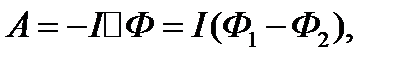
где Ф1 – магнитный поток, пронизывающий контур до перемещения, Ф2 – то же, после перемещения.
Если 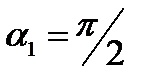 ,то Ф1=ВS, Ф2=0. Следовательно,
,то Ф1=ВS, Ф2=0. Следовательно,
А = IBS = IBa2,
что совпадает с выражением (1).
2) Воспользуемся выражением для механической потенциальной энергии контура с током в магнитном поле.
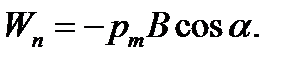
Тогда работа внешних сил
А=ΔWп = W2 - W1,
или
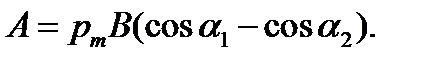
Так как рm= Ia2, cosα1=1 и cosα2=0, то
A=IBa2,
что также совпадает с выражением (1)
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ

 A
A  A
A  A
A  A
A