Примеры решения задач. Пример1.Квадратная рамка со стороной а и длинный прямой провод с током J находятся в одной плоскости

Пример1.Квадратная рамка со стороной а и длинный прямой провод с током J находятся в одной плоскости, как показано на рис.3.1. Рамку поступательно перемещают вправо с постоянной скоростью v. Найти ЭДС индукции в рамке как функцию расстояния х.

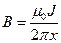Индукция магнитного поля на расстоянии х от оси прямого проводника с током определяется выражением (см. пример 2п.2.1.1). Учитывая, что вектор магнитной индукции перпендикулярен плоскости рамки, магнитный поток, пронизывающий плоскость рамки, будет равным:

,

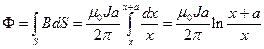где x = vt.

Тогда ЭДС индукции в рамке e_i .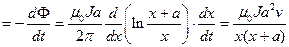

Пример 2.Найти собственные частоты колебаний w_1,2двух индуктивно связанных контурах с емкостями С₁ = С₂ = С, индуктивностями L₁ = L₂ = L и коэффициентом взаимной индукции L₁₂

Рис. 3.2

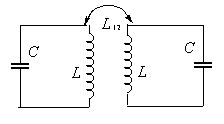Пусть сила тока в первом контуре J₁ и во втором - J₂. В соответствии с законом Ома в цепи переменного тока (3.8) и (3.9) составим систему уравнений

,

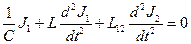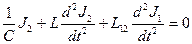
Рис.3.2 Будем искать решение системы в виде

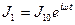и .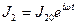

Подстановка решения в исходные уравнения позволяет перейти от системы дифференциальных уравнений к системе линейных однородных алгебраических уравнени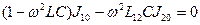й:

и .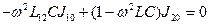

Такая система имеет нетривиальное решение, если детерминант, составленный из коэффициентов при неизвестных, равен нулю, т.е.

,

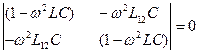или .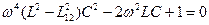

Действительные положительные корни этого уравнения определяют частоты собственных колебаний контуров: .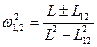

Таким образом, в системе двух одинаковых индуктивно связанных колебательных контуров реализуются собственные колебания с частотам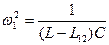и

и .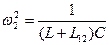

Если L₁₂ << L, то колебания контуров – независимы, с собственными частотами 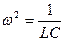. Если же связь сильная, и L₁₂ >> L, то в системе реализуются колебания с одной частотой .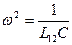