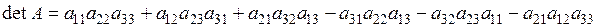Правила обчислення визначників різних порядків
| Визначник першого порядку: | 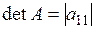 | ||
Визначник дорівнює самому елементу: 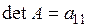 | |||
| Визначник другого порядку: | 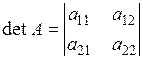 | ||
а) визначник дорівнює різниці добутків елементів головної та побічної діагоналі: 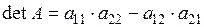 | |||
б) розкладання визначника за елементами будь-якого рядка (стовпця): 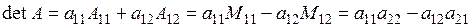 | |||
| Визначник третього порядку: | 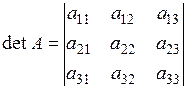 | ||
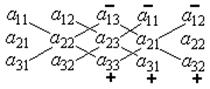
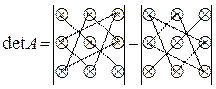 а) правило „трикутника”: якщо елементи матриці позначити точками, то співмножники трьох додатних доданків лежать на головній діагоналі та у вершинах трикутників, одна із сторін яких паралельна головній діагоналі. Аналогічні співмножники від’ємних доданків лежать на побічній діагоналі та у вершинах трикутників, одна із сторін яких паралельна їй: а) правило „трикутника”: якщо елементи матриці позначити точками, то співмножники трьох додатних доданків лежать на головній діагоналі та у вершинах трикутників, одна із сторін яких паралельна головній діагоналі. Аналогічні співмножники від’ємних доданків лежать на побічній діагоналі та у вершинах трикутників, одна із сторін яких паралельна їй: 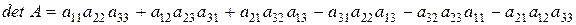 | |||
|
Продовження
в) розкладання визначника за елементами будь-якого рядка (стовпця): наприклад, розкладання за елементами 1 рядка: 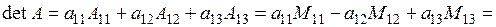 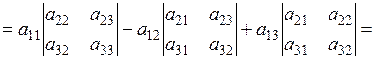 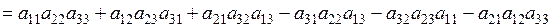 | |
| Визначник n-го порядку: | 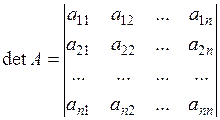 |
а) метод зниження порядку: визначник матриці 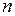 -го порядку дорівнює сумі добутків усіх елементів якого-небудь одного фіксованого рядка на їх алгебраїчне доповнення, тобто для будь-якого -го порядку дорівнює сумі добутків усіх елементів якого-небудь одного фіксованого рядка на їх алгебраїчне доповнення, тобто для будь-якого 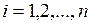 має місце рівність: має місце рівність: 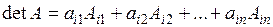 , яка має назву розкладання визначника за елементами , яка має назву розкладання визначника за елементами 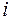 -го рядка. Аналогічно для -го рядка. Аналогічно для 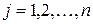 має місце розкладання визначника по елементам має місце розкладання визначника по елементам 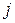 -го стовпця: -го стовпця: 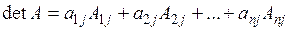 . Це дозволяє знизити порядок обчислювальних визначників і в кінцевому рахунку звести задачу до знаходження визначників 3-го порядку. Зауваження. Якщо в деякому рядку (стовпці) початкового визначника багато нулів, то саме по ньому зручно проводити розкладання. Більш того, використовуючи властивості визначників, можна добитися того, що всі елементи деякого рядка (стовпця), крім одного, будуть дорівнювати нулю . Це дозволяє знизити порядок обчислювальних визначників і в кінцевому рахунку звести задачу до знаходження визначників 3-го порядку. Зауваження. Якщо в деякому рядку (стовпці) початкового визначника багато нулів, то саме по ньому зручно проводити розкладання. Більш того, використовуючи властивості визначників, можна добитися того, що всі елементи деякого рядка (стовпця), крім одного, будуть дорівнювати нулю | |
б) метод зведення до трикутного вигляду: використовуючи властивості визначників, досягають такої структури визначника, при якій всі його елементи, які розташовані вище (нижче) головної діагоналі, дорівнюють нулю, тобто визначник має трикутну форму і чисельно дорівнює добутку елементів, що розташовані на головній діагоналі: 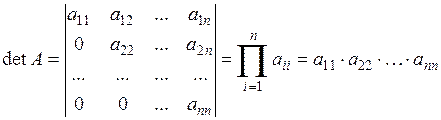 |
Властивості визначників
| 1. Значення визначника не зміниться при його транспонуванні (рядки та стовпці визначника еквівалентні) | 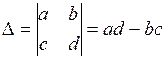 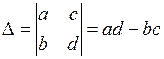 |
| 2. Якщо у визначнику поміняти місцями два сусідні рядки чи стовпці, то знаки таких визначників будуть протилежними, а їх абсолютні значення – однаковими | 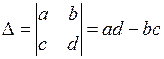 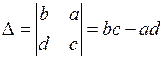 |
3. Якщо деякий ряд визначника помножити на довільне число 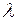 , то значення визначника зміниться у , то значення визначника зміниться у 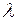 разів. І навпаки: множник, що є спільним для елементів деякого ряду, можна винести за знак визначника разів. І навпаки: множник, що є спільним для елементів деякого ряду, можна винести за знак визначника | 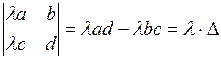 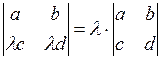 |
| 4. Якщо всі елементи деякого рядка чи стовпця визначника дорівнюють нулю, то і сам визначник дорівнює нулю | 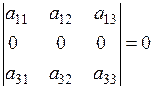 |
| 5. Визначник із двома однаковими рядками чи стовпцями дорівнює нулю | 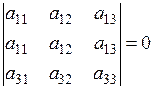 |
| 6. Значення визначника не зміниться, якщо до будь-якого його ряду додати інший, помножений на довільне число або лінійну комбінацію інших рядів | 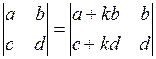 |
| 7. Сума добутків елементів будь-якого ряду визначника на алгебраїчні доповнення, які відповідають елементам іншого паралельного ряду, дорівнює нулю | 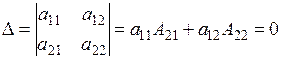 |
| 8. Якщо кожен елемент деякого ряду визначника дорівнює сумі двох доданків, то цей визначник дорівнює сумі двох визначників, причому в першому відповідний ряд складається з перших доданків, а в другому – з других доданків | 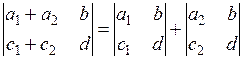 |
Обернена матриця
Матриця 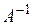 називається оберненою до матриці
називається оберненою до матриці 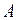 , якщо виконується умова:
, якщо виконується умова: 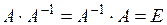 .
.
Для того, щоб квадратна матриця 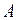 мала обернену матрицю, необхідно і достатньо, щоб її визначник не дорівнював нулю (невироджена матриця). Обернену матрицю можливо знайти наступним чином:
мала обернену матрицю, необхідно і достатньо, щоб її визначник не дорівнював нулю (невироджена матриця). Обернену матрицю можливо знайти наступним чином:
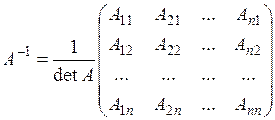 , , |
де 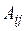 – алгебраїчні доповнення елементів
– алгебраїчні доповнення елементів 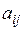 визначника матриці
визначника матриці 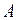 .
.
Зауваження. Звернемо увагу на розташування чисел 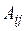 в правій частині формули: число
в правій частині формули: число 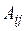 розташоване не у
розташоване не у 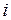 -му рядку та
-му рядку та 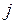 -му стовпці, а навпаки, в
-му стовпці, а навпаки, в 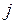 -му рядку та
-му рядку та 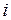 -му стовпці. Таким чином, матриця, що розташована в правій частині, є транспонованою матрицею алгебраїчних доповнень елементів матриці
-му стовпці. Таким чином, матриця, що розташована в правій частині, є транспонованою матрицею алгебраїчних доповнень елементів матриці 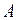 .
.
1.3. Системи лінійних алгебраїчних рівнянь (СЛАР)
Лінійним (відносно невідомих 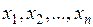 ) називають алгебраїчне рівняння першого порядку, тобто рівняння виду
) називають алгебраїчне рівняння першого порядку, тобто рівняння виду 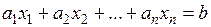 , де
, де 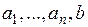 – числа. Так рівняння першого ступеня з двома змінними
– числа. Так рівняння першого ступеня з двома змінними 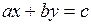 визначає на площині в декартовій прямокутній системі координат пряму лінію.
визначає на площині в декартовій прямокутній системі координат пряму лінію.
Система 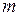 лінійних рівнянь з
лінійних рівнянь з 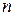 невідомими в загальному випадку записується наступним чином:
невідомими в загальному випадку записується наступним чином:
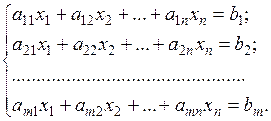
В загальному випадку число рівнянь в системі не обов’язково співпадає з числом невідомих: 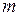 може бути менше, більше числа
може бути менше, більше числа 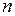 або дорівнювати йому.
або дорівнювати йому.
Числа 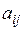 (дійсні або комплексні) називаються коефіцієнтами системи;
(дійсні або комплексні) називаються коефіцієнтами системи; 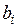 – вільними членами;
– вільними членами; 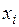 – невідомими (
– невідомими ( 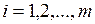 ,
, 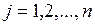 ).
).
Систему можна записати в матричній формі:
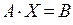 :
:
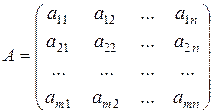 , , |  , , | 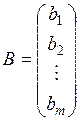 . . |
| основна матриця системи | матриця-стовпець невідомих | матриця-стовпець вільних членів |
Розв’язком СЛАР називається впорядкована сукупність 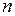 чисел (
чисел ( 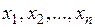 ), які при підстановці в систему замість невідомих, перетворюють усі рівняння в тотожності.
), які при підстановці в систему замість невідомих, перетворюють усі рівняння в тотожності.

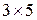 . Тоді додатні та від’ємні доданки формули будують за схемою:
. Тоді додатні та від’ємні доданки формули будують за схемою: