Доказательство теоремы синусов

Построим произвольный треугольник, вписанный в окружность. Обозначим его как ABC.
Для доказательства всей теоремы, поскольку размеры треугольника выбраны произвольным образом, достаточно доказать, что соотношение одной произвольной стороны к противолежащему ей углу равно 2R. Пусть это будет 2R = a / sin α, то есть если взять по чертежу 2R = BC / sin A.

Проведем диаметр BD для описанной окружности. Образовавшийся треугольник BCD является прямоугольным, поскольку его гипотенуза лежит на диаметре описанной окружности (свойство углов, вписанных в окружность).

Поскольку, углы, вписанные в окружность, опирающиеся на одну и ту же дугу, равны, то угол CDB либо равен углу CAB (если точки A и D лежат по одну сторону от прямой BC), либо равен π - CAB (в противном случае).

Обратимся к свойствам тригонометрических функций. Поскольку sin( π − α ) = sin α, то указанные варианты построения треугольника все равно приведут к одному результату.

Вычислим значение 2R = a / sin α, по чертежу 2R = BC / sin A. Для этого заменим sin A на соотношение соответствующих сторон прямоугольного треугольника.

2R = BC / sin A
2R = BC / ( BC / DB )
2R = DB

А, поскольку, DB строился как диаметр окружности, то равенство выполняется.
Повторив то же рассуждение для двух других сторон треугольника, получаем:

Теорема синусов доказана.

Теорема синусов

Примечание. Это часть урока с задачами по геометрии (раздел теорема синусов). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение.

Теорема синусов:
Стороны треугольника пропорциональны синусам противолежащих углов, или, в расширенной формулировке:
a / sin α = b / sin β = c / sin γ = 2R
где R - радиус описанной окружности

Теорию - формулировку и доказательство теоремы подробно см. в главе "Теорема синусов".

Задача

В треугольнике XYZ угол Х=30 угол Z=15. Перпендикуляр YQ к ZY делит сторону ХZ на части XQ и QZ.Найти XY, если QZ=1.5м

Решение.
Высота образовала два прямоугольных треугольника XYQ и ZYQ.
Для решения задачи воспользуемся теоремой синусов.
QZ / sin( QYZ ) = QY / sin( QZY )

QZY = 15 градусов, Соответственно, QYZ = 180 - 90 - 15 = 75

Примем во внимание табличные значения некоторых тригонометрических функций:

• синус 15 градусов равен sin( 15 ) =
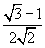
• синус 75 градусов равен sin( 75 ) =

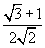
(или то же самое "при записи в одну строку") QZ / sin( 75 ) = QY / sin( 15 ) QZ / ( ( √3 + 1 ) / ( 2√2 ) ) = QY / ( ( √3 - 1 ) / ( 2√2 ) ) QZ * 2√2 / ( √3 + 1 ) = QY * 2√2 / ( √3 - 1 ) 3√2 ( √3 - 1 ) = QY * 2√2 ( √3 + 1 ) QY = 3√2 ( √3 - 1 ) / ( 2√2 ( √3 + 1 ) ) QY = 3/2 (√3 - 1 ) / (√3 + 1 )

Поскольку длина высоты треугольника теперь известна, найдем XY по той же теореме синусов.

QY / sin( 30 ) = XY / sin( 90 )

Примем во внимание табличные значения некоторых тригонометрических функций:

• синус 30 градусов равен sin( 30 ) = 1 / 2
• синус 90 градусов равен sin( 90 ) = 1

тогда

QY = XY sin ( 30 )
3/2 ( √3 - 1 ) / ( √3 + 1 ) = 1/2 XY
XY = 3 ( √3 - 1 ) / ( √3 + 1 ) ≈ 0.8 м

Ответ: 0,8 м или 3 ( √3 - 1 ) / ( √3 + 1 )

Теорема синусов (часть 2)

Примечание. Это часть урока с задачами по геометрии (раздел теорема синусов). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме .

Теорию подробно см. в главе "Теорема синусов".

Задача

Сторона АВ треугольника ABC равна 16см. Угол А равен 30 градусам. Угол В равен 105 градусам. Вычислите длину стороны ВС.

Решение.
Согласно теореме синусов, стороны треугольника пропорциональны синусам противолежащих углов:
a / sin α = b / sin β = c / sin γ

Таким образом
BC / sin α = AB / sin γ

Величину угла С найдем, исходя из того, сумма углов треугольника равна 180 градусам.
С = 180 - 30 -105 = 45 градусов.

Откуда:
BC / sin 30° = 16 / sin 45°

BC = 16 sin 30° / sin 45°

Обратившись к таблице тригонометрических функций, находим:

BC = ( 16 * 1 / 2 ) / √2/2 = 16 / √2 ≈ 11,3 см

Ответ: 16 / √2

Задача.
В треугольнике ABC угол А = α, угол С = β, ВС = 7см, ВН - высота треугольника.
Найти АН

Решение.
Для решения задачи воспользуемся теоремой синусов. Из нее следует, что:

BC / sin α = AB / sin β

то есть
7 / sin α = AB / sin β
AB = 7 sin β / sin α

Теперь рассмотрим треугольник ABH. По условию задачи BH - высота, значит он является прямоугольным. Угол AHB = 90 градусам.
Тогда угол ABH = 180 - 90 - α. = 90 - α.
Для него будет верно соотношение:

AB / sin 90 = AH / sin (90 - α)

Из таблицы значений тригонометрических функций учтем что sin 90 = 1, тогда

AB = AH / sin (90 - α)

Из формул приведения тригонометрических функций учтем что sin( 90 - α ) = cos α, тогда

AB = AH / cos α

Подставим значение AB

7 sin β / sin α = AH / cos α
AH sin α = 7 sin β cos α
AH = 7 sin β cos α / sin α

Из тех же тригонометрических тождеств выясним, что cos α / sin α = ctg α, тогда

AH = 7 sin β ctg α

Ответ: 7 sin β ctg α

Теорема косинусов