Определение производной функции через предел
Пусть в некоторой окрестности точки 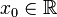 определена функция
определена функция 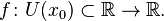 Производной функции
Производной функции 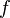 в точке
в точке 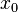 называется предел, если он существует,
называется предел, если он существует,
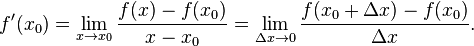
Общепринятые обозначения производной функции 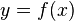 в точке
в точке 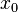
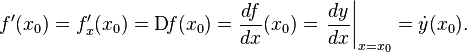
Таблица производных
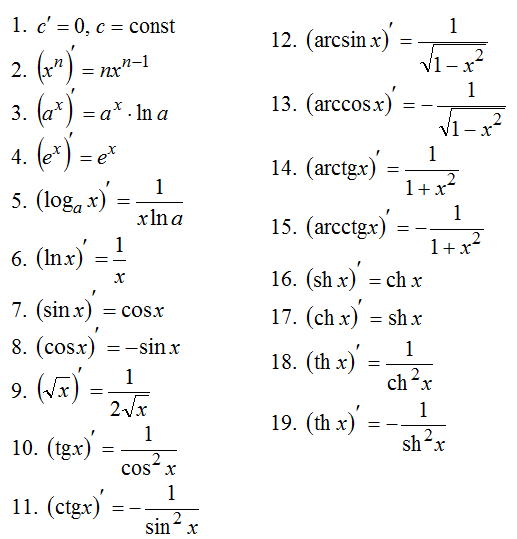

Геометрический смысл производной функции в точке.
Рассмотрим секущую АВ графика функции y=f(x) такую, что точки А и В имеют соответственно координаты 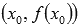 и
и 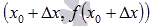 , где
, где 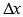 - приращение аргумента. Обозначим через
- приращение аргумента. Обозначим через 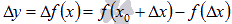 приращение функции. Отметим все на чертеже:
приращение функции. Отметим все на чертеже:
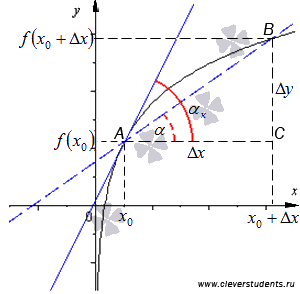
Из прямоугольного треугольника АВС имеем 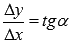 . Так как по определению касательная – это предельное положение секущей, то
. Так как по определению касательная – это предельное положение секущей, то 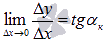 .
.
Вспомним определение производной функции в точке: производной функции y=f(x)в точке 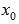 называется предел отношения приращения функции к приращению аргумента при
называется предел отношения приращения функции к приращению аргумента при 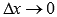 , обозначается
, обозначается 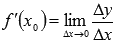 .
.
Следовательно, 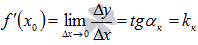 , где
, где 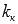 - угловой коэффициент касательной.
- угловой коэффициент касательной.
Таким образом, существование производной функции y=f(x) в точке 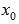 эквивалентно существованию касательной к графику функции y=f(x) в точке касания
эквивалентно существованию касательной к графику функции y=f(x) в точке касания 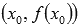 , причем угловой коэффициент касательной равен значению производной в точке
, причем угловой коэффициент касательной равен значению производной в точке 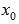 , то есть
, то есть 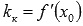 .
.
Заключаем: геометрический смысл производной функции в точке состоит в существовании касательной к графику функции в этой точке.
20 Дифференцируемость функции в точке. Необходимое и достаточное условие дифференцируемости.
Приращение дифференцируемой в данной точке функции можно представить как линейную функцию приращения аргумента с точностью до величин более высокого порядка малости. Это означает, что для достаточно малых окрестностей данной точки функцию можно заменить линейной (скорость изменения функции можно считать неизменной). Линейная часть приращения функции называется ее дифференциалом (в данной точке).
Необходимым, но не достаточным условием дифференцируемости является непрерывность функции. В случае функции от одной вещественной переменной дифференцируемость равносильна существованию производной. В случае функции нескольких вещественных переменных необходимым (но не достаточным) условием дифференцируемости является существование частных производных по всем переменным. Для дифференцируемости функции нескольких переменных в точке достаточно, чтобы частные производные существовали в некоторой окрестности рассматриваемой точки и были непрерывны в данной точке.[1]
21 Дифференцируемость функции в точке. Теорема о непрерывности дифференцируемой функции.
Теорема.
Если функция в данной точке дифференцируема, то в этой точке функция непрерывна.
Доказательство.
Пусть функция y=f(x)y=f(x) дифференцируема в точке x0x0, тода приращение этой функии равно Δy=A⋅Δx+α(Δx)⋅xΔy=A⋅Δx+α(Δx)⋅x.
При стремлении приращения аргумента функции ΔxΔx к нулю приращение функции ΔyΔyтакже стремится к нулю, а это и означает непрерывность функции.
То есть в итоге мы получили, что функция y=f(x)y=f(x), дифференцируемая в точке x0x0, является в этой точке и непрерывной функцией. Что и требовалось доказать.
Таким образом непрырывность функции в данной точке является необходимым, но недостаточным условием для дифференцируемости функции.
Пример.
Функция y=|x|y=|x| в точке x0x0 является непрерывной функцией, но в этой точке функция не дифференцируема.
Действительно, приращение функии равно:
Δy=f(x0+Δx)−f(x0)=|Δx|Δy=f(x0+Δx)−f(x0)=|Δx|.
При этом получаем:
ΔyΔx=|Δx|Δx={1,Δx>0,−1,Δx<0ΔyΔx=|Δx|Δx={1,Δx>0,−1,Δx<0.
Предел limΔx→0ΔyΔxlimΔx→0ΔyΔx не существует, а значите функцкия y=|x|y=|x|, непрерывная в точке x0x0, не дифференцируема в этой точке.
22 Дифференциал функции. Геометрический смысл дифференциала.
Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Это записывается так:
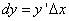
или
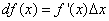
или же
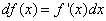
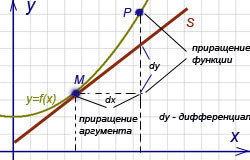
Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину 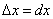 (см. рисунок)..
(см. рисунок)..
23 Правило дифференцируемости суммы и произведения.
Для доказательства второго правила дифференцирования 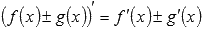 воспользуемся определением производной и свойством предела непрерывной функции.
воспользуемся определением производной и свойством предела непрерывной функции.
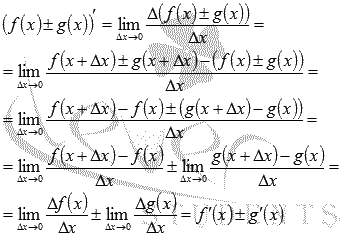
Подобным образом можно доказать, что производная суммы (разности) n функций равна сумме (разности) n производных
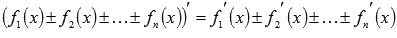 .
.
Докажем правило дифференцирования произведения двух функций 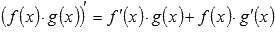 .
.
Запишем предел отношения приращения произведения функций к приращению аргумента. Будем учитывать, что 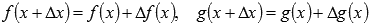 и
и 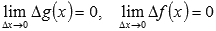 (приращение функции стремиться к нулю при приращении аргумента, стремящемся к нулю).
(приращение функции стремиться к нулю при приращении аргумента, стремящемся к нулю).
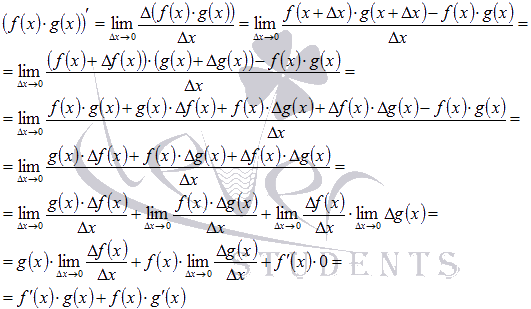
Что и требовалось доказать.
24 Инвариантность формы 1 дифференциала.
Инвариантность формы первого дифференциала
Если x - независимая переменная, то dx = x - x0 (фиксированное приращение). В этом случае имеем
df(x0) = f'(x0)dx. (3)
Если x = φ(t) - дифференцируемая функция, то dx = φ'(t0)dt. Следовательно,
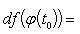
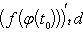
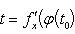
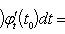
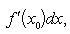
т. е. первый дифференциал обладает свойством инвариантности относительно замены аргумента.
25 Теорема Ролля.
Теорема Ро́лля (теорема о нуле производной) утверждает, что
Если вещественная функция, непрерывная на отрезке 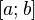 и дифференцируемая на интервале и дифференцируемая на интервале 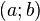 , принимает на концах отрезка , принимает на концах отрезка 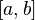 одинаковые значения, то на интервале одинаковые значения, то на интервале 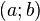 найдётся хотя бы одна точка, в которой производная функции равна нулю. найдётся хотя бы одна точка, в которой производная функции равна нулю. |
Доказательство
Если функция на отрезке постоянна, то утверждение очевидно, поскольку производная функции равна нулю в любой точке интервала.
Если же нет, поскольку значения функции в граничных точках сегмента равны, то согласно теореме Вейерштрасса, она принимает своё наибольшее или наименьшее значение в некоторой точке интервала, то есть имеет в этой точке локальный экстремум, и по Лемме Ферма, в этой точке производная равна 0.
Геометрический смысл
Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.

26 Теорема Лагранжа и ее следствия.
Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция 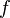 непрерывна на отрезке
непрерывна на отрезке 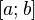 и дифференцируема в интервале
и дифференцируема в интервале 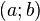 , то найдётся такая точка
, то найдётся такая точка 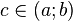 , что
, что
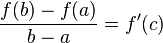 .
.
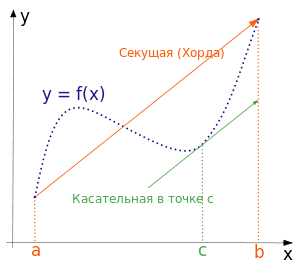
Геометрически это можно переформулировать так: на отрезке 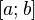 найдётся точка, в которой касательнаяпараллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
найдётся точка, в которой касательнаяпараллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
Механическое истолкование: Пусть 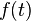 — расстояние точки в момент
— расстояние точки в момент 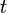 от начального положения. Тогда
от начального положения. Тогда 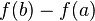 есть путь, пройденный с момента
есть путь, пройденный с момента 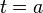 до момента
до момента 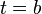 , отношение
, отношение 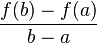 — средняя скорость за этот промежуток. Значит, если скорость тела определена в любой момент времени
— средняя скорость за этот промежуток. Значит, если скорость тела определена в любой момент времени 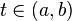 , то в некоторый момент она будет равна своему среднему значению на этом участке.
, то в некоторый момент она будет равна своему среднему значению на этом участке.
Доказательство
Для функции одной переменной:
Введем функцию 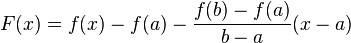 . Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны нулю. Воспользовавшись упомянутой теоремой, получим, что существует точка
. Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны нулю. Воспользовавшись упомянутой теоремой, получим, что существует точка  , в которой производная функции
, в которой производная функции 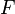 равна нулю:
равна нулю:
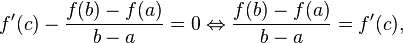
что и требовалось доказать.
Следствия и обобщения
Теорема Лагранжа о конечных приращениях - одна из самых важных, узловая теорема во всей системе дифференциального исчисления. Она имеет массу приложений в вычислительной математике, и главнейшие теоремы математического анализа также являются её следствиями.
Следствие 1. Дифференцируемая на отрезке функция с производной, равной нулю, есть константа.
Доказательство. Для любых 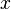 и
и 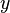 существует точка
существует точка  , такая что
, такая что 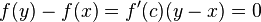 .
.
Значит, при всех 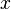 и
и 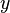 верно равенство
верно равенство 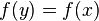 .
.
Следствие 2 (Формула Тейлора с остаточным членом в форме Лагранжа). Если функция 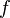 дифференцируема
дифференцируема 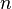 раз в окрестности точки
раз в окрестности точки 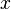 , то для малых
, то для малых 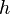 (т.е. тех, для которых отрезок
(т.е. тех, для которых отрезок 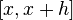 лежит в указанной окрестности) справедлива формула Тейлора:
лежит в указанной окрестности) справедлива формула Тейлора:
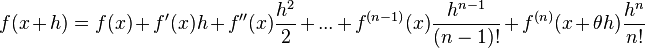
где 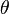 - некоторое число из интервала
- некоторое число из интервала 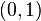 .
.
Следствие 3. Если функция 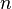 переменных
переменных 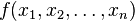 дважды дифференцируема в окрестности точки О и все её вторые смешанные производные непрерывны в точке О, тогда в этой точке справедливо равенство:
дважды дифференцируема в окрестности точки О и все её вторые смешанные производные непрерывны в точке О, тогда в этой точке справедливо равенство: 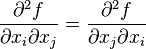
Доказательство для 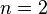 . Зафиксируем значения
. Зафиксируем значения 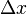 и
и 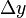 и рассмотрим разностные операторы
и рассмотрим разностные операторы
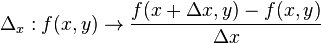 и
и 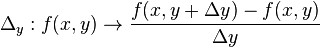 .
.
По теореме Лагранжа существуют числа 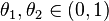 , такие что
, такие что
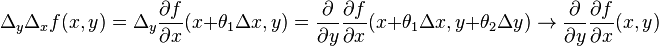
при 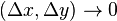 в силу непрерывности вторых производных функции
в силу непрерывности вторых производных функции 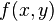 .
.
Аналогично доказывается, что 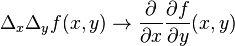 .
.
Но так как 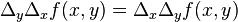 , (что проверяется непосредственно), то эти пределы совпадают.
, (что проверяется непосредственно), то эти пределы совпадают.
Следствие 4 (Формула Ньютона-Лейбница). Если функция 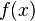 дифференцируема на отрезке
дифференцируема на отрезке 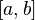 и её производная интегрируема по Риману на этом отрезке, то справедлива формула:
и её производная интегрируема по Риману на этом отрезке, то справедлива формула: 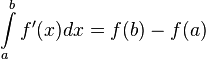 .
.
Доказательство. Пусть 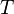 - произвольное разбиение
- произвольное разбиение 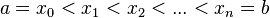 отрезка
отрезка 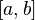 . Применяя теорему Лагранжа, на каждом из отрезков
. Применяя теорему Лагранжа, на каждом из отрезков 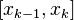 найдём точку
найдём точку 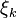 такую, что
такую, что 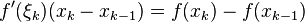 .
.
Суммируя эти равенства, получим: 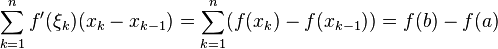
Слева стоит интегральная сумма Римана для интеграла 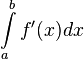 и заданного отмеченного разбиения. Переходя к пределу по диаметру разбиения, получим формулу Ньютона-Лейбница.
и заданного отмеченного разбиения. Переходя к пределу по диаметру разбиения, получим формулу Ньютона-Лейбница.
Следствие 5 (Теорема об оценке конечных приращений). Пусть отображение 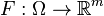 непрерывно дифференцируемо в выпуклой компактной области
непрерывно дифференцируемо в выпуклой компактной области 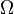 пространства
пространства 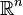 . Тогда
. Тогда 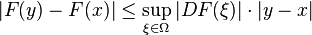 .
.
27 Теорема Каши.
Теорема Коши́ о среднем значении.
Пусть даны две функции 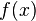 и и 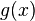 такие, что: 1. такие, что: 1. 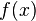 и и 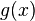 определены и непрерывны на отрезке определены и непрерывны на отрезке 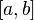 ; 2. производные ; 2. производные 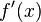 и и 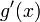 конечны на интервале конечны на интервале 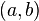 ; 3. производные ; 3. производные 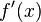 и и 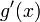 не обращаются в нуль одновременно на интервале не обращаются в нуль одновременно на интервале 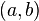 4. 4. 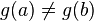 ; тогда существует ; тогда существует 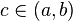 , для которой верно: , для которой верно: 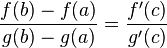 . (Если убрать условие 4, то необходимо, например, усилить условие 3: g'(x) не должна обращаться в ноль нигде в интервале . (Если убрать условие 4, то необходимо, например, усилить условие 3: g'(x) не должна обращаться в ноль нигде в интервале 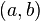 .) .) |
Геометрически это можно переформулировать так: если 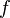 и
и 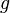 задают закон движения на плоскости (то есть определяют абсциссу и ординату через параметр
задают закон движения на плоскости (то есть определяют абсциссу и ординату через параметр 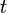 ), то на любом отрезке такой кривой, заданном параметрами
), то на любом отрезке такой кривой, заданном параметрами 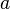 и
и 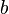 , найдётся касательный вектор, коллинеарный вектору перемещения от
, найдётся касательный вектор, коллинеарный вектору перемещения от 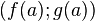 до
до 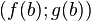 .
.
Доказательство
Для доказательства введём функцию
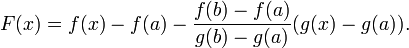 |
Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны 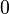 . Воспользовавшись упомянутой теоремой, получим, что существует точка
. Воспользовавшись упомянутой теоремой, получим, что существует точка  , в которой производная функции
, в которой производная функции 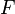 равна нулю, а
равна нулю, а 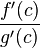 равна как раз необходимому числу.
равна как раз необходимому числу.
28 Формула Тейлора.
Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.
Теорема:
Если функция 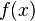 имеет имеет 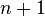 производную на отрезке с концами производную на отрезке с концами 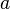 и и 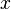 , то для произвольного положительного числа , то для произвольного положительного числа 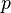 найдётся точка найдётся точка 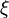 , лежащая между , лежащая между 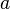 и и 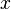 , такая, что , такая, что 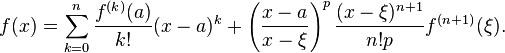 |
