Особенности геометрии и условия работы косозубых цилиндрических передач. Длина линии контакта и распределение нагрузки по длине контакта

У косозубого колеса расстояние между зубьями можно мерить в торцовом сечении и нормальном сечении. В первом случае получают окружной шаг P_t, во втором нормальный шаг P.

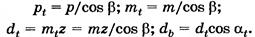
Помимо торцевого у косозубых передач есть еще осевое перекрытие 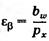, где P_x – осевой шаг, равный расстоянию между одноименными точками двух смежных зубьев измеренному в направлении оси колеса.

Особенности геометрии определяют отличия условий работы косозубой передачи:

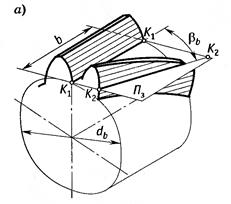
1) линия контакта на косозубом колесе расположены || оси вращения под углом θ к полюсной линии

2) в отличие от прямозубой в косозубой передаче зубья входят в зацепление не сразу по все длине, а постепенно. Увеличивается время контакта одной пары зубьев. Чем больше угол наклона линии зуба, тем выше плавность в зацеплении.

3) нагрузка по длине контактной линии распределяется пропорционально суммарной жесткости зубьев шестерни и колеса. При контакте одним из сопряженных зубьев в вершине жесткость меньше и нагрузка меньше.

4) в косозубой передаче в зацеплении участвуют одновременно 2-3 пары зубьев, поэтому суммарная длина контактных линий больше, чем у прямозубых.

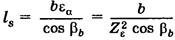
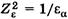
5)Соотношение между радиусами кривизны контактирующих зубьев в косозубой передаче более благоприятно .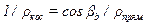

43. Понятие "приведенное зубчатое колесо" и приведенное число зубьев косозубых цилиндрических колес. Коэффициент, учитывающий форму зуба косозубого цилиндрического зубчатого колеса.

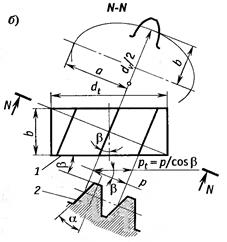
Расчетным является сечение N — N, нормальное к направ­лению зуба. В этом сечении определяют пара­метры эквивалентного колеса, которые используются при рас­чете на прочность. Профиль зуба косозубого колеса соответст­вует профилю эквивалентного прямозубого колеса с радиусом, равным радиусу кривизны эллипса по малой оси 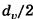. Боль­шая полуось эллипса 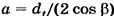, малая — 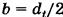, радиус кривизны 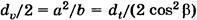. Так как диаметр эквива­лентного прямозубого колеса 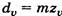, то эквивалентное число зубьев

,

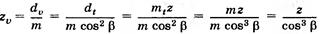Где z –число зубьев косозубого колеса. При расчете на прочность косозубые колеса заменяют на прямозубые с эквивалентным числом зубьев. С увеличением угла β эквивалентные параметры возрастают, что способствует повышению прочности передачи.

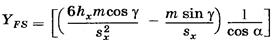
Коэффициент формы зуба не зависит от размеров зубьев, уменьшается с увеличением коэффициента смещения исходного контура x и с увеличением эквивалентного числа зубьев z_v.

Особенности расчета косозубых и шевронных колес на сопротивление контактной и изгибной усталости. Чем обуславливается повышение нагрузочной способности косозубых и шевронных передач по сравнению с прямозубыми.

Контактная усталость:

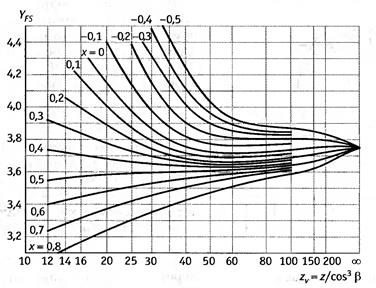
В косозубых и шевронных передачах зубья входят в зацепление постепенно. Расчет проводят с учетом геометрии в сечении, нормальном к направлению зуба. Результирующая сила в нормальной плоскости на делительной окружности 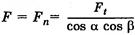. Суммарная длина контактных линий 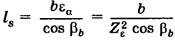, 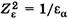. Радиус кривизны эвольвенты в полюсе зацепления в нормальном сечении .

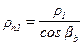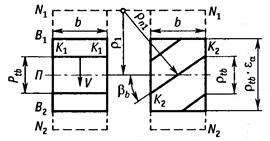
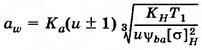
Ψ_ab – коэффициент относительной ширины колеса, K_H – коэффициент нагрузки. Условие контактной прочности 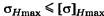, максимальное расчетное напряжение 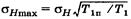, T_1П – максимальный вращающий момент на шестерне, T₁ – вращающий момент на шестерне, принятый при расчетах на выносливость при изгибе.

На изгибную усталость:

Для косозубых и шевронных передач характерно повышенное сопротивление усталости при изгибе.

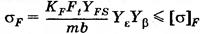
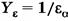- коэффициент, учитывающий торцевое перекрытие.

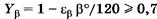- коэффициент, учитывающий наклон зуба, получен экспериментально. 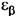- коэффициент осевого перекрытия.

Прочность зубьев при однократной нагрузке .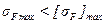

Максимальные расчетные напряжения 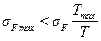, T_max – максимальный вращающий момент на шестерне, T – вращающий момент на шестерне, принятый при расчетах на выносливость при изгибе.