Формулы полной вероятности
Пусть событие А может произойти в результате осуществления одного события из некоторой полной группы событий:
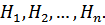
События этой группы обычно называют гипотезами.
Тогда
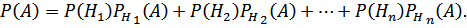
(формула полной вероятности), причем
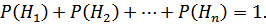
Пример 5
В магазин для продажи поступает продукция трех предприятий в следующих относительных долях: I– 40 %, II– 50 %,III– 10 %. Для продукции этих предприятий брак соответственно составляет: I– 5 %, II– 6 %, III– 1 %. Найти вероятность того, что изделие этой продукции, случайно приобретенное в магазине, окажется доброкачественным.
Решение.Обозначим: А – случайное приобретенное изделие –доброкачественное; 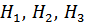 – приобретенное изделие изготовлено соответственно на I, II, и III предприятиях. Согласно условию:
– приобретенное изделие изготовлено соответственно на I, II, и III предприятиях. Согласно условию:
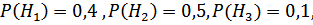
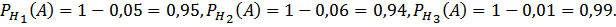
По формуле полной вероятности получаем:
s w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>A</m:t></m:r></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>=0,4в€™0,95+0,5в€™0,94+0,1в€™0,99=0,949. </m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 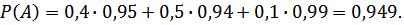
Пусть в результате испытания произошло событие А, которое могло наступить только вместе с одним из событий 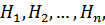 образующих полную группу событий. Требуется найти вероятность событий
образующих полную группу событий. Требуется найти вероятность событий 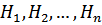 после испытания, когда событие А уже имело место, т. е.
после испытания, когда событие А уже имело место, т. е. 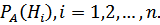 Для нахождения этих вероятностей используют формулы Байеса (формулы гипотез):
Для нахождения этих вероятностей используют формулы Байеса (формулы гипотез):
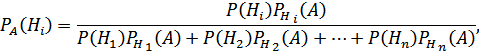
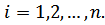
Пример 6
В условиях примера 5 найти вероятность того, что купленное в магазине и оказавшееся доброкачественным изделие произведено на втором предприятии.
Решение
По формуле Байеса:
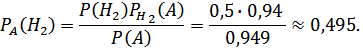
Формула Бернулли
Пусть проводится серия из п испытаний, в результате каждого из которых событие А может произойти или не произойти. Предполагаем, что вероятностьp наступления события А в каждом испытании постоянна, т. е. не зависит ни от номера испытания, ни от результатов предыдущих испытаний. Последовательность испытаний, удовлетворяющих указанному условию, называется последовательностью независимых испытаний (или схемой Бернулли).
Таким образом, в схеме Бернулли для каждого испытания имеется лишь два исхода:
1) событие А, 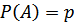 ;
;
2) противоположное событие 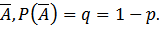
Вероятность 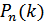 того, что в серии из п испытаний в схеме Бернулли событие А наступит ровно k раз (безразлично в какой последовательности), выражается формулой Бернулли
того, что в серии из п испытаний в схеме Бернулли событие А наступит ровно k раз (безразлично в какой последовательности), выражается формулой Бернулли
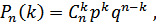 где
где 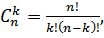
Вероятность того, что в п испытаниях событие наступит: а) менее k раз; б) более k раз; в) не менее k раз; г) не более k раз находят соответственно по формулам:
a) 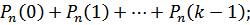
б) 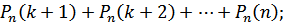
в) 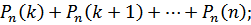
г) 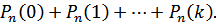
Пример 7
Что вероятнее, выиграть у равносильного противника 2 партии из 4 или 3 из 6?
Решение
Используя формулу Бернулли при п=4, k=2, 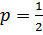 , ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
, ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 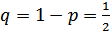 , находим
, находим
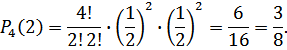
Затем при п=6, 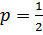 ,
, 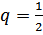 , находим
, находим
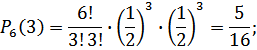
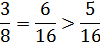
следовательно, вероятнее выиграть 2 партии из 4.
Варианты контрольных работ
Задача 1. (Теоремы сложения и умножения вероятностей)
1.1. В двух партиях 80 % и 90 % доброкачественных изделий соответственно. Наудачу выбирают по данному изделию из каждой партии. Какова вероятность обнаружения среди них: а) хотя бы одною бракованного; б) двух бракованных; в) одного доброкачественного и одного бракованного?
1.2. Вероятность того, что цель будет поражена первым стрелком, равна 0, 7, вторым - 0, 6. Найти вероятность того, что в цель попадет только
один стрелок.
1.3. В ящике 4 белых и 5 черных шаров. Извлекают 3 шара. Какова вероятность того, что все извлеченные шары: а) белые; б) черные.
1.4. В цехе работают 6 мужчин и 4 женщины. Наудачу отобраны 3 человека. Найти вероятность того, что все отобранные – мужчины.
1.5. Вероятность поражения цели первым стрелком равна 0,8, а вторым – 0,6. Определить вероятность того, что: а) цель поражена хотя бы одним стрелком; б) цель не поражена при условии, что стрелки произвели независимо друг от друга по одному выстрелу.
1. 6. В магазин поступило 30 телевизоров, 5 среди которых имеют скрытые дефекты. Наудачу отбирают 2 телевизора для проверки. Какова вероятность, что они оба не имеют дефектов?
1.7. В ящике имеется 12 деталей, среди которых 8 окрашенных. Сборщик наудачу извлекает две детали. Найти вероятность того, что обе извлеченные детали окажутся окрашенными.
1.8. Вероятность безотказной работы двух независимо работающих сигнализаторов соответственно равна 0, 6 и 0, 7. Найти вероятность того, что сработают: а) оба сигнализатора; б) хотя бы один сигнализатор.
1. 9. На полке стоят 10 книг, из которых 4 книги без переплета. Наудачу взяты две книги. Найти вероятность того, что обе взятые книги: а) без переплета; б) в переплете.
1. 10. Вероятность того, что 1–й студент сдаст экзамен равна 0,8, второй – 0,7. Найти вероятность того, что: а) оба студента сдадут экзамен;
б) хотя бы один студент сдаст экзамен.
1. 11. Изделия проверяются на стандартность. Вероятность того, что изделие стандартно равно 0, 8. Найти вероятность тою, что из двух проверенных изделий только одно стандартно.
1. 12.Устройство содержит два независимо работающих элемента. Вероятности отказов элементов соответственно равны 0, 05 и 0, 08. Найти вероятность отказа устройства, если для этого достаточно отказа хотя бы одного элемента.
1.13. Среди 1000 лотерейных билетов 4 выигрышных. Найти вероятность того, что 3 наудачу выбранных билета являются выигрышными.
1. 14. Студент знает 20 вопросов из 25. Найти вероятность того, что студент знает предложенные ему экзаменатором 3 вопроса.
1. 15. В группе из 20 студентов четверо не подготовились к занятию. Наудачу вызваны два студента. Какова вероятность того, что они оба готовы к занятию?
1. 16. Партия товара, состоящая из 15 ящиков, подлежит приемке, если при проверке наугад двух выбранных ящиков окажется, что содержащиеся в них изделия удовлетворяют стандарту. Найти вероятность приемки партии, содержащей в 5 ящиках нестандартные изделия.
1. 17. Для некоторой местности число пасмурных дней в июле равно 6, найти вероятность того, что 1 и 2 июля наудачу выбранного года будет ясная погода.
1.18. Два спортсмена должны выполнить норму мастера спорта. Вероятность того, что первый спортсмен выполнит норму, равна 0, 9, второй – 0,8. Найти вероятность того, что норма будет выполнена: а) обоими спортсменами; б) хотя бы одним спортсменом.
1.19. Два спортсмена участвуют в отборочных соревнованиях. Вероятность зачисления в сборную команду первого и второго спортсменов соответственно равны 0, 8; 0, 6. Найти вероятность того, что хотя бы один из спортсменов попадет в сборную.
1.20. Два студента ищут нужную им книгу в книжных магазинах. Вероятность того, что книга будет найдена первым студентом, равна 0, 5, вторым - 0, 7. Какова вероятность того, что только один из студентов найдет
книгу?
1.21. Баскетболист производит два штрафных броска. Вероятность попадания мяча в корзину при каждом броске равна 0, 7. Найти вероятность следующих событий: а) два попадания мяча корзину; б) хотя бы одно попадание.
1.22. Два орудия производят залп по цели. Вероятность попадания в цель первого орудия равна 0, 8, второго – 0,7. Найти вероятности следующих событий: а) два попадания в цель; б) хотя бы одно попадание.
1.23.Экспедиция издательства отправила газеты в два почтовых отделения. Вероятность современной доставки в первое отделение равна 0, 9, во второе– 0, 8. Найти вероятности следующих событий: а) оба отделения получили газеты вовремя; б) только одно отделение получило газеты вовремя.
1.24. Студент знает 50 из 60 вопросов программы. Найти вероятность того, что студент знает два вопроса, содержащиеся в его экзаменационном билете.
1. 25. В одном ящике 5 белых и 10 черных шаров, в другом ящике 10 белых и 5 черных шаров. Найти вероятность того, что хотя бы из одного ящика будет вынут один белый шар, если из каждого ящика вынуто по одному шару.
1. 26. Вероятность того, что в течение одной смены возникнет неполадка станка, равна 0, 5. Найти вероятность того, что не произойдет ни одной неполадки за три смены.
1. 27. В ящике 10 красных и 5 зеленых пуговиц. Вынимаются наугад две пуговицы. Какова вероятность того, что пуговицы будут одноцветными?
1. 28. Два охотника стреляют в волка, причем каждый делает по одному выстрелу. Для первого охотника вероятность попадания в цель равна 0, 7, для второго – 0, 6. Какова вероятность попадания в волка хотя бы при одном выстреле?
1. 29. Из троллейбусного депо в случайном порядке последовательно выходят три троллейбуса маршрута № 1 и семь троллейбусов № 2. Найти вероятность того, что вторым по порядку выйдет на линию троллейбус № 2, а первым – троллейбус № 1.
1. 30. На складе телевизионного ателье из имеющихся 20 кинескопов 6 изготовлены заводом № 1, остальные - заводом № 2. Найти вероятность того, что два наудачу взятых кинескопа изготовлены заводом № 1.
Задача 2. (Формула полной вероятности и формулы Байеса)
2. 1. Вероятности посещения трех магазинов одинаковы. Вероятность того, что в первом магазине есть необходимый товар, равна 0, 7, во втором–0, 6, а в третьем –0, 5. Найти вероятность того, что нужный товар будет куплен.
2. 2. В условиях задачи 2. 1 в результате посещения магазина нужный товар куплен. Найти вероятность того, что покупка произведена во втором магазине.
2. 3. С одинаковой вероятностью студент может уехать на одном из трех видов транспорта. Вероятность того, что он приедет вовремя на автобусе, равна 0, 8, на трамвае – 0, 6, на троллейбусе – 0, 7. Найти вероятность того, что студент вовремя приедет на занятия.
2. 4. В условиях задачи 2.3 студент вовремя приехал на занятия. Найти вероятность того, что он приехал на трамвае.
2. 5. В первой урне 6 белых шаров, во второй – 3 белых и 3 черных, а в третьей – 5 белых и один черный. Из взятой на удачу урны извлечен один шар. Найти вероятность того, что он – черный.
2. 6. В условиях задачи 2.5 извлечен черный шар. Найти вероятность того, что он извлечен из третьей урны.
2. 7. В урне лежит шар неизвестного цвета – с равной вероятностью черный или белый. В урну опускается один белый шар и после тщательного перемешивания наудачу извлекается один шар. Какова вероятность того, что он окажется черным?
2. 8. Два автомата производят детали, которые поступают на общий конвейер. Вероятность получения нестандартной детали на первом автомате равна 0, 06, на втором – 0, 02. Производительность первого автомата втрое больше, чем второго. Найти вероятность того, что наудачу взятая с конвейера деталь нестандартна.
2. 9. В условиях задачи 2. 8 взятая с конвейера деталь оказалась не стандартной. Найти вероятность того, что она изготовлена первым автоматом.
2. 10. Имеется три партии товара:
–в первой партии 10 % бракованных изделий;
–во второй – 20 %;
–в третьей – нет бракованных изделий.
Наудачу извлечено одно изделие из наудачу взятой партии. Найти вероятность того, что оно – бракованное.
2. 11. В условиях задачи 2. 10 извлеченное изделие оказалось бракованным. Найти вероятность того, что оно извлечено из первой партии.
2. 12. В цехе два конвейера, с которых сходят одинаковые детали и сбрасываются в общую кучу. Вероятность того, что деталь с первого
конвейера нестандартна, равна 0, 04, со второго - 0, 07. Производительность первого конвейера в два раза больше производительности второго. Какова вероятность того, что произвольно взятая из кучи деталь окажется нестандартной?
2. 13. В условиях задачи 2.12 взятая деталь оказалась нестандартной. Найти вероятность того, что она сошла со второго конвейера.
2. 14. В двух колодах по 36 карт. Из первой колоды наудачу вынимается карта и кладется во вторую колоду, из которой затем после перемешивания вынимается наудачу одна карта. Найти вероятность того, что эта карта бубновой масти.
2. 15. В условиях задачи 2. 14 из второй колоды была вынута карта бубновой масти. Найти вероятность того, что из первой колоды была вынута тоже карта бубновой масти.
2. 16. Число автобусов и троллейбусов относится как 3:2. Вероятность вовремя приехать на автобусе, равна 0, 8, на троллейбусе – 0, 7. Найти вероятность того, что опоздания не будет.
2. 17. В условиях задачи 2.16 опоздания не произошло. Найти вероятность того, что путь был проделан на автобусе.
2. 18. Сообщение можно передать письмом, по телефону и с оказией с одинаковой вероятностью. Вероятность того, что сообщение дойдет в каждой из перечисленных возможностей, соответственно равны 0, 7; 0, 6; 0, 8. Какова вероятность доставки сообщения?
2. 19. В условиях задачи 2. 18 сообщение доставлено. Найти вероятность того, что оно передано по телефону.
2. 20. В группе 25 студентов. Из них отличников– 4, хорошистов – 6, троечников – 12, остальные – двоечники. Вероятность сдачи экзамена отличником равна 0, 95, хорошистом – 0, 8, троечником – 0, 6. двоечником –0, 3. Какова вероятность того, что произвольно вызванный студент сдаст экзамен?
2. 21. В условиях задачи 2. 20 найти вероятность того, что сдавший экзамен студент – двоечник.
2. 22. Поломка прибора может быть вызвана одной из трех причин, вероятности которых соответственно равны 0, 7; 0, 2; 0, 1. При наличии этих причин поломка происходит соответственно с вероятностями 0, 1; 0, 2; 0, 2, найти вероятность того, что прибор выйдет из строя.
2. 23. В условиях задачи 2. 22 произошла поломка прибора. Найти вероятность того, что она произошла по второй причине.
2. 24. Из 1000 ламп 300 принадлежат первой партии, 500 –второй и 200– третьей. В первой партии 6%, во второй 5% и в третьей 4% бракованных ламп. Определить вероятность того, что взятая наудачу одна лампа – бракованная.
2. 25. В условиях задачи 2. 24 извлеченная лампа оказалась бракованной. Найти вероятность того, что она принадлежит второй партии.
2. 26. В первой урне 3 белых и 5 черных шаров, во второй 4 белых и 2 черных шара. Из первой урны извлекается один шар и опускается во вторую. Какова вероятность вынуть белый шар из второй урны после того?
2. 27. В условиях задачи 2. 26 вынутый шар оказался белым. Найти вероятность того, что из первой урны тоже был вынут белый ряд.
2. 28. В магазин одновременно поступают изделия с трех заводов: 30% с первого, 50% со второго, 20% с третьего. Среди изделий первого завода 80% первосортных, второго – 90%, третьего – 70%. Куплено одно изделие. Определить вероятность того, что оно первосортное.
2. 29. В условиях задачи 2. 28 найти вероятность того, что купленное первосортное изделие изготовлено на третьем заводе.
2. 30. В ящике два шара. Равновозможны все случаи их сочетания по цвету. В ящик опускается белый шар, а затем после перемешивания наудачу извлекается один шар. Найти вероятность того, что он белый.
Задача 3. (Повторение испытаний: формулы Бернулли и Пуассона, локальная и интегральная теоремы Лапласа)
3. 1. Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0, 1. Найти вероятность двух «сбоев» при шести вызовах.
3. 2. Вычислить вероятность того, что при 100 бросаниях монет «орел» выпадет 10 раз.
3.3. Вероятность появления события А в одном испытании равна 0, 4. Произведено 5 испытаний. Найти вероятность того, что событие А наступит не более одного раза.
3. 4. Вероятность наступления события А в одном испытании равна 0,6. Найти вероятность того, что в четырех испытаниях оно наступит не менее двух раз.
3. 5. Завод выпускает изделия, из которых 80% стандартных. Какова вероятность при отборе 100 изделий обнаружить ровно 18 нестандартных?
3. 6. Вероятность появления события А в одном испытании равна 0, 4. Произведено 4 испытания. Что вероятнее, что событие наступит два раза или не менее трех раз?
3. 7. Вероятность появления события А в одном испытании равна 0, 2. Найти вероятность того, что в 100 испытаниях событие А появится не менее 30 раз и не более 40 раз.
3. 8. Вероятность появления события А в каждом из 2100 независимых испытаний равна 0, 7. Найти вероятность того, что событие появится не менее 1470 раз.
3. 9. Среди 1000 лотерейных билетов есть 4 выигрышных. Найти вероятность того, что три наудачу взятых билета окажутся выигрышными.
3.10. Известно, что в данном селе 80% семей имеют телевизоры. Найти вероятность того, что среди 6 случайно отобранных семей 2 окажутся без телевизора.
3. 11. Вероятность того, что в течение дня расход воды не превысит норму, равна 0, 75. Найти вероятность того, что расход воды будет нормальным в течение четырех из пяти дней.
3. 12. В каждом из 2000 независимых испытаний вероятность появления события А равна 0, 0005. Найти вероятность того, что событие А наступит ровно 2 раза.
3. 13. При каждом выстреле из орудия вероятность поражения цели равна 0, 6. Найти вероятность того, что при пяти выстрелах будет три промаха.
3. 14. Вероятность появления бракованных деталей равна 0, 008. Найти вероятность того, что из 500 случайно отобранных деталей окажется 3 бракованных.
3. 15. Вероятность поражения мишени при одном выстреле равна 0, 8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.
3. 16. Найти вероятность того, что в 400 независимых испытаниях событие А наступит не менее 190 и не более 215 раз, если вероятность появления события в одном испытании равна 0, 5.
3. 17. Вероятность появления события в одном испытании равна 0, 9. Найти вероятность того, что в 100 испытаниях событие наступит ровно 80 раз.
3. 18. Найти вероятность того, что в 400 испытаниях событие А наступит не менее 290 раз и не более 330 раз, если вероятность события А в одном испытании равна 0, 8.
3. 19. Вероятность наступления события А в одном испытании равна 0,9. Найти вероятность того, что в 100 испытаниях событие А наступит не менее 80 раз.
3. 20. Вероятность выживания бактерий после радиоактивного излучения равна 0, 004. Найти вероятность того, что после облучения 500 бактерий останется менее 3 выживших.
3. 21. Книга издана тиражом 50000 экземпляров. Вероятность того, что в книге дефект брошюровки равен 0, 0001. Найти вероятность того, что тираж содержит 5 неправильно брошюрованных книг.
3. 22. Вероятность появления события в каждом из 625 испытаний равна 0, 64. Найти вероятность того, что событие появится не менее 430 и не более 450 раз.
3. 23. Вероятность появления события в каждом из 100 независимых испытаний равна 0, 8. Найти вероятность того, что событие появится не менее 75 и не более 90 раз.
3. 24. Рабочий за смену изготавливает 400 деталей. Вероятность того, что деталь окажется первого сорта, равна 0, 8. Какова вероятность того, что деталей первого сорта будет ровна 330?
3. 25. Найти вероятность того, что событие А наступит 1400 раз в 2400 испытаниях, если вероятность появления этого события в каждом испытании равна 0, 6.
3. 26. Устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа любого элемента в течение часа равна 0, 002. Найти вероятность того, что за час откажут 4 элемента.
3. 27. Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна 0, 01. Телефонная станция обслуживает 800 абонентов. Какова вероятность того, что в течение часа позвонят 5 абонентов?
3. 28. Что вероятнее выиграть у равносильного противника (ничьи исключены): три партии из четырех или пять из восьми?
3. 29. Вероятность появления события в каждом испытании равна 0, 25. Найти вероятность того, что в 300 испытаниях событие наступит ровно 75 раз.
3. 30. Хлебозавод выпускает 90% продукций первого сорта. Какова
вероятность того, что из 400 изделий хлебозавода первосортных окажется не
менее 380?
Задача 4. (Числовые характеристики дискретных случайных величин)
Найти:
а) математическое ожидание M(X);
б) дисперсию D(X);
в) среднее квадратическое отклонение σ(X) дискретной случайной величины X по данному закону распределения.
4.1.
| X | -3 | |||
| p | 0,1 | 0,2 | 0,4 | 0,3 |
4.2.
| X | ||||
| p | 0,1 | 0,5 | 0,2 | 0,2 |
4.3.
| X | ||||
| p | 0,3 | 0,2 | 0,1 | 0,4 |
4.4.
| X | -3 | -2 | ||
| p | 0,1 | 0,5 | 0,2 | 0,2 |
4.5.
| X | ||||
| p | 0,4 | 0,3 | 0,1 | 0,2 |
4.6.
| X | -3 | -2 | ||
| p | 0,1 | 0,2 | 0,5 | 0,2 |
4.7.
| X | ||||
| P | 0,1 | 0,6 | 0,1 | 0,2 |
4.8.
| X | -4 | -2 | ||
| p | 0,4 | 0,2 | 0,1 | 0,3 |
4.9.
| X | ||||
| p | 0,5 | 0,1 | 0,1 | 0,3 |
4.10.
| X | ||||
| p | 0,1 | 0,4 | 0,3 | 0,2 |
4.11.
| X | -4 | -2 | -1 | |
| p | 0,1 | 0,4 | 0,3 | 0,2 |
4.12.
| X | ||||
| p | 0,3 | 0,2 | 0,1 | 0,4 |
4.13.
| X | ||||
| p | 0,3 | 0,1 | 0,5 | 0,1 |
4.14.
| X | -2 | -1 | ||
| p | 0,1 | 0,6 | 0,1 | 0,2 |
4.15.
| X | -3 | -2 | ||
| p | 0,3 | 0,2 | 0,1 | 0,4 |
4.16.
| X | -6 | -1 | ||
| p | 0,2 | 0,1 | 0,5 | 0,2 |
4.17.
| X | ||||
| p | 0,4 | 0,1 | 0,2 | 0,3 |
4.18.
| X | -3 | -1 | ||
| p | 0,2 | 0,4 | 0,1 | 0,3 |
4.19.
| X | -1 | |||
| p | 0,3 | 0,5 | 0,1 | 0,1 |
4.20.
| X | ||||
| p | 0,2 | 0,4 | 0,1 | 0,3 |
4.21.
| X | ||||
| p | 0,3 | 0,4 | 0,2 | 0,1 |
4.22.
| X | -4 | -3 | -1 | |
| p | 0,4 | 0,1 | 0,1 | 0,4 |
4.23.
| X | ||||
| p | 0,3 | 0,1 | 0,2 | 0,4 |
4.24.
| X | -4 | |||
| p | 0,3 | 0,1 | 0,2 | 0,4 |
4.25.
| X | -2 | |||
| p | 0,3 | 0,4 | 0,1 | 0,2 |
4.26.
| X | -6 | -2 | ||
| p | 0,4 | 0,2 | 0,1 | 0,3 |
4.27.
| X | ||||
| p | 0,1 | 0,1 | 0,2 | 0,6 |
4.28.
| X | -5 | -3 | ||
| p | 0,2 | 0,2 | 0,1 | 0,5 |
4.29.
| X | ||||
| p | 0,1 | 0,2 | 0,1 | 0,6 |
4.30.
| X | ||||
| p | 0,2 | 0,1 | 0,3 | 0,4 |
Задача 5. (Непрерывные случайные величины)
Случайная величинаXзадана функцией распределения F(х).
Найти:
а) функцию плотности распределения f(х);
б) математическое ожидание M(X);
в) дисперсию D(Х) и среднее квадратическое отклонениеσ(Х);
г) построить график функций F(х) иf(х).
5.1. 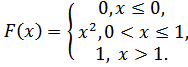 5.2.
5.2. 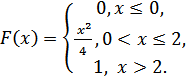
5.3. 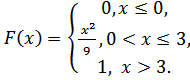 5.4.
5.4. 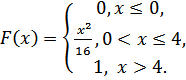
5.5. 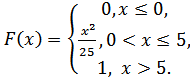 5.6.
5.6. 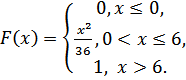
5.7. 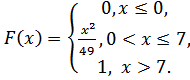 5.8.
5.8. 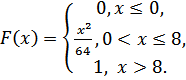
5.9. 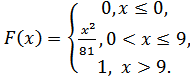 5.10.
5.10. 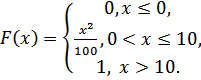
5.11. 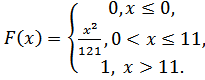 5.12.
5.12. 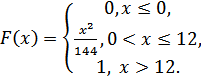
5.13. 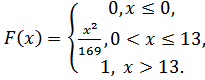 5.14.
5.14. 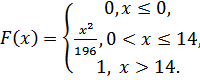
5.15. 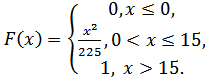 5.16.
5.16. 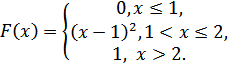
5.17. 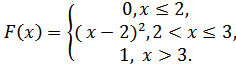 5.18.
5.18. 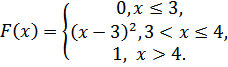
5.19. 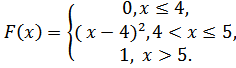 5.20.
5.20. 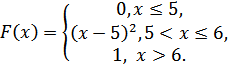
5.21. 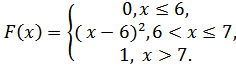 5.22.
5.22. 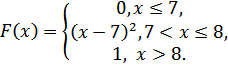
5.23. 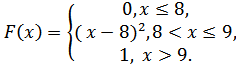 5.24.
5.24. 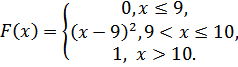
5.25. 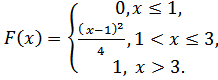 5.26.
5.26. 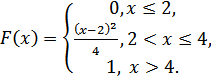
5.27. 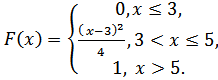 5.28.
5.28. 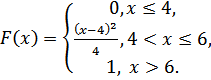
5.29. 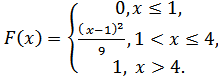 5.30.
5.30. 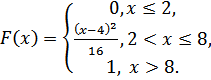
Задача 6. (Законы распределения случайных величин)
Для случайной величины Х, распределенной равномерно на отрезке [а, b],написать функцию распределения F(x), плотность вероятности f(х), Найти математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение σ(Х), если задан отрезок:
6.1. [1,5]; 6. 2. [2,6];
6.3. [4, 8]; 6.4. [0, 5];
6. 5. [9, 11]; 6.6. [8, 10];
6. 7. [4,9]; 6. 8. [3,13];
6. 9. [1,6]; 6. 10. [10,15].
Для случайной величины X, распределенной по нормальному закону, известны математическое ожидание М(Х) и дисперсия D(Х). Записать плотность вероятности f(х) и найти вероятность попадания случайной величины X в интервал (α,β):
6. 11. М(Х)=1, D(Х)=1, (2, 4); 6. 12. М(Х)=2, D(Х)=4, (1, 5);
6. 13. М(Х)=3, D(Х)=4, (2, 6); 6. 14. М(Х)=2, D(Х)=9, (1, 3);
6. 15. М(Х)=5, D(Х)=4, (3, 7); 6. 16. М(Х)=6, D(Х)=16, (4, 7);
6. 17. М(Х)=1, D(Х)=4, (0, 3); 6. 18. М(Х)=3, D(Х)=16, (1, 5);
6. 19. М(Х)=8, D(Х)=4, (5, 10); 6. 20. М(Х)=4, D(Х)=9, (2, 7).
Случайная величина X распределена по показательному закону, заданному плотностью вероятности:
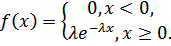
Написать плотность вероятности f(х), функцию распределения F(x). Найти математическое ожидание М(Х), дисперсию D(Х )и среднее квадратическое отклонение σ(Х), если λ равно:
6.21. 1; 6.22. 2;
6.23. 4; 6.24. 5;
6.25. 8; 6.26. 10;
6.27. 0,5; 6.28. 0,25;
6.29. 0,1; 6. 30. 0,125.
Математическая статистика
Задание на самостоятельную работу
Используя данные выборки (см. приложение), решить следующие подзадачи:
1. Составить вариационный ряд (таблица 1).
2. Вычислить относительные частоты, округлить цифры до
четырехзначных, в сумме должны получить 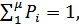 где v – число интервалов.
где v – число интервалов.
3. Вычислить накопленные частости и все внести в таблицу 1.
4. Построить графики вариационного ряда (полигон и гистограмму).
5. Составить эмпирическую (интегральную) функцию распределения и построить её график.
6. Вычислить числовые характеристики вариационного ряда и описать их назначение: среднеарифметическое 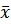 ; дисперсию
; дисперсию 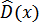 ; среднеквадратичное отклонение; моду; медиану; эксцесс; коэффициент асимметрии.
; среднеквадратичное отклонение; моду; медиану; эксцесс; коэффициент асимметрии.
7. Произвести оценки числовых характеристик генеральной совокупности, используя результаты расчета части 1. Определить несмещенные точечные оценки: математического ожидания Mx; дисперсии Dx; среднеквадратичного отклонения Gx.
8. Принять гипотезу о нормальном распределении генеральной совокупности признака и записать функцию плотности распределения вероятности с учетом найденных параметров.
9. Вычислить теоретические частоты нормального распределения, результаты вычислении оформить таблицей.
10. Вычислить эмпирическое (наблюдаемое) значение c2 и составить расчетную таблицу.
11. Найти критическое значение c2кр в таблице по данным: К – число степеней свободы и a – уровень значимости.
12. Сделать вывод о приемлемости выбранной гипотезы.
13. Найти доверительные интервалы для математического ожидания, дисперсии и среднеквадратичного отклонения для доверительной вероятности 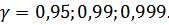 (в случае, если гипотеза о нормальном распределении подтверждается).
(в случае, если гипотеза о нормальном распределении подтверждается).
