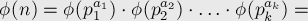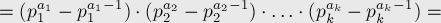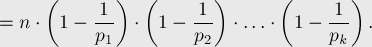Теоремы о функции Эйлера: мультипликативность;

Теория чисел.

1. Деление с остатком. Свойства НОД.
Для любого а ϵ Zи для любого b ϵ Nсуществует q ϵ Z, такое, что .
Замечание: остаток r определён однозначно.
Свойства НОД.
1) mϵN, (am,bm)=(a,b)m
2) если в - общий делитель чиселaи b, то:
Замечание: если в качестве делителя ввзять НОД(a,b) чисел, то получим:

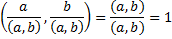
2. Алгоритм Евклида(АЕ). Линейное представление НОД.
Пусть a и b ϵN:
1) b|a→(a,b)=b
2) пусть b не делит a →a=bq+r₂, 0<=r<b
для единообразия обозначим: r₀=r₁q₁+r₂, 0<=r₂<r₁.
Рассмотрим:
r₁=r₂q₂+r₃, 0<=r₃<r₂
продолжаем делить с остатком:
r₂=r₃q₃+r₄ (предпоследний на последний)
…
r_n-2=r_n-1q_n-1+r_n, 0<=r_n<r_n-1
r_n-1=r_nq_n+0.
Линейное представление НОД:
пусть d(a,b) – НОД, тогда существуют целые числа M и N: d=Ma+Nb.
Замечание: наименьший положительный элемент из совокупности значений ma+nb, m,n ϵ Z является НОД.

3. Свойства НОД.
Свойства НОД.
1) mϵN, (am,bm)=(a,b)m
2) если в - общий делитель чиселaи b, то:
Замечание: если в качестве делителя ввзять НОД(a,b) чисел, то получим:

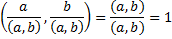
4. Свойства взаимной простоты.
Числа a и b называют взаимно-простыми, если их НОД=1.
1) (a,b)=1→Ǝ M,N: Ma+Nb=1
2) (a₁,b)=1 и (a₂,b)=1, то (a₁a₂, b)=1
3) если каждое из чисел a₁,…,a_n взаимно-просто с каждым из чисел с b₁,…,b_k, то взаимно просты их произведения: (a₁,…,a_n, b₁,…,b_k)=1
4) если c|ab и (c,a)=1, то c|b.

5. Делимость на простое число. Бесконечность множества простых чисел.
Натуральное число p называется простым, если у него нет делителей, кроме 1 и самого p.
Т.Каждое натуральное число делится на некоторое число.
Теорема Евклида: множество простых чисел бесконечно.

6. Делимость произведения на простое число. Основная теорема арифметики.
Т. Если p|ab, то по крайней мере одно из чисел a, либо b делится на p.
Теорема об однозначном разложении на простые множители(основная теорема арифметики): всякое число a может быть представлено в виде произведения простых множителей и при том единственным образом с точность до порядка следования элементов.
Пример: 210=2*105=2*3*35=2*3*5*7.
Пример: 108=2²*3³.

7. Разложение НОД и НОК на простые множители. Связь НОД и НОК.
НОД
Пример:
a=2³*5¹*3²=360
b=3*2²*7=84
(a,b)=2²*5⁰3¹*7⁰=4*3=12.
НОК целых чисел a₁,…,a_n называется наименьшее положительное число M, которое делится на каждое из них.
Обозначение: M=m(a₁,…,a_n).
Теорема о связи НОД и НОК:
НОД(a,b)*m(a,b)=a*b.

8. Разложение числа в непрерывную дробь(НД). Подходящие дроби.
Если число элементов конечно, то значением дроби является рациональное число, как результат арифметических действий с рациональными числами. (сигма )
Подходящей дробью – в сопоставлению числу α, НД, указанным способом называются числа:
Замечания:
1) Можно доказать, что для иррационального числа α бесконечная последовательность подходящей дроби имеет пределом само число α, то есть α раскладывается в бесконечную непрерывную дробь.
2)Каждая следующая подходящая дробь получается из предыдущей заменой самого нижнего q_i на q_i+1/q_i+1.
3)Равенство α=б₁ означает, что непрерывная дробь конечна и α – рациональное число.

9. Подходящие дроби: рекуррентные формулы; свойства.
Свойства ПД.
1)P_iQ_i-1-Q_iP_i-1=(-1)ⁱ
2)при i>=Z: б_i-б_i-1=(-1)ⁱ/Q_i*Q_i-1
3)(P_i,Q_i)=1
4) если число не совпадает со своей ПД (α≠б_i), то зн(б_i-α)=зн(-1).

10. Показатели простых множителей n!.
Т.Простой множительp ,входящий в разложение n! …[n/p]+[n/p²]+[n/p³]…
Пример:
51! p=3
[51/3]+[51/3²]+[51/3³]+[51/81]

11. Общие свойства мультипликативных функций.
N называется мультипликативной, если:
1) она не является тождественно нулевой;
2) если a и b взаимно просты.
Мультипликативная функция полностью определяется своими значениями на степенях простых чисел.
Обратно, создавая произвольным образом значения на степенях простых чисел получаем мультипликативную функцию.

12. Мультипликативность функции Мёбиуса.
Функция Мёбиуса(μ(n)) задаётся на нат. Чисел правилом:
1) μ(1)=1
2) если n>1 и n делится на квадрат простого числа, то μ(n)=0
3) если все простые множители входят в разложение числа n первой степени и их количество равно
k, то μ(n)=(-1)^k.

Теоремы о функции Эйлера: мультипликативность; .

Определение

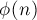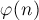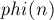Функция Эйлера (иногда обозначаемая или ) — это количество чисел от 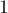до 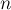, взаимно простых с 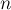. Иными словами, это количество таких чисел в отрезке 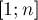, наибольший общий делитель которых с 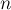равен единице.

Несколько первых значений этой функции (A000010 в энциклопедии OEIS):

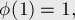
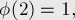
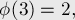
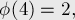
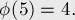
Свойства

Три следующих простых свойства функции Эйлера — достаточны, чтобы научиться вычислять её для любых чисел:

· Если 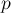— простое число, то .

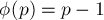(Это очевидно, т.к. любое число, кроме самого 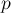, взаимно просто с ним.)

· Если 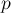— простое, 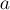— натуральное число, то .

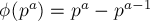(Поскольку с числом 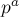не взаимно просты только числа вида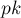 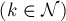, которых 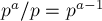штук.)

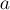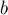· Если и взаимно простые, то 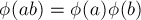("мультипликативность" функции Эйлера).

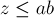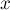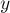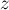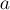(Этот факт следует из китайской теоремы об остатках. Рассмотрим произвольное число . Обозначим через и остатки от деления на и 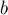соответственно. Тогда 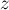взаимно просто с 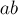тогда и только тогда, когда 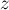взаимно просто 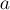с и с 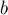по отдельности, или, что то же самое, 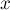взаимно просто с 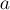и 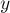взаимно просто с 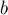. Применяя китайскую теорему об остатках, получаем, что любой паре чисел 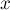и 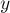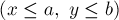взаимно однозначно соответствует число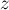 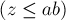, что и завершает доказательство.)

Отсюда можно получить функцию Эйлера для любого 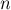через его факторизацию (разложение 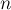на простые сомножители):

если

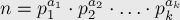
(где все 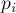— простые), то