Задачи по теории вероятностей
1. 12 студентов случайным образом рассаживаются на 12 первых местах одного ряда партера. Какова вероятность того, что студенты М и Н будут сидеть рядом?
2. В ящике находится 20 лампочек, среди которых 3 перегоревшие. Найти вероятность того, что 10 лампочек, взятых наудачу из ящика, будут гореть.
3. Действительные числа х и у удовлетворяют системе неравенств: -1 ≤ х ≤ 3 и 2 ≤ у ≤ 5. Какова вероятность того, что они удовлетворяют также системе: 0 ≤ х ≤ 1
и 3 ≤ у ≤ 4?
4. На АТС могут поступать вызовы трёх типов. Вероятности поступления вызовов 1-ого, 2-ого и 3-его типа соответственно равны: 0.2, 0.3, 0.5. Поступило три вызова. Какова вероятность того, что а) все они разных типов; б) среди них нет вызова 2-ого типа?
5. В пункте проката имеется 8 новых и 10 подержанных (т.е. хотя бы раз использованных) автомобилей. Три машины взяли наудачу в прокат и, спустя некоторое время, вернули. После этого вновь наудачу взяли в прокат два автомобиля. Какова вероятность того, что оба автомобиля новые?
6. Завод отправил на базу 5000 изделий. Вероятность того, что в пути изделие повредится, равна 0.0002. Найти вероятность того, что а) на базу прибудет ровно три и
б) не более трех изделий.
7. 9 туристов наудачу рассаживаются по 12 вагонам электрички. Найти вероятность того, что все они окажутся: а) в одном вагоне; б) во втором вагоне;
в) в разных вагонах.
8. Имеются три урны. В первой урне 3 белых и 2 синих шара, во второй-4 белых, 3 синих и 5 черных шаров, в третьей-2 белых, 2 синих и 3 черных шара. Из выбранной урны взяли три шара. Найти вероятность того, что они разных цветов.
9. В автопарке 20 экскурсионных автобусов двух марок: 12 и 8 соответственно. Вероятность выезда на экскурсию автобусов каждой марки одна и та же.
4 автобуса выехали на экскурсию. Какова вероятность того, что выехали автобусы: а) первой марки; б) одной марки; в) разных марок?
10. Сумма квадратов двух неотрицательных чисел не больше 64. Какова вероятность того, что их сумма не больше 8?
11. С вероятностью 0.4 посланное сообщение принимается при одной передаче. Сколько надо сделать передач, чтобы с вероятностью не менее 0.9 сообщение было принято хотя бы один раз?
12. На ёлочный базар поступают ёлки с трех лесхозов, причем первый лесхоз поставил 50% ёлок, второй – 30%, третий – 20%. Среди ёлок первого лесхоза 10% голубых, второго – 20%, третьего – 30%. Куплена одна ёлка. Она оказалась голубой. Какова вероятность того, что она поставлена вторым лесхозом?
13. Вероятность поражения мишени при одном выстреле равна 0.8. Найти вероятность того, что при 100 выстрелах мишень будет поражена не менее 75 раз.
14. В семизначном телефонном номере стерлись три последние цифры. Найти вероятность того, что стерлись: а) одинаковые цифры; б) разные цифры.
15. В урне находится 40 шаров. Вероятность того, что два извлеченных шара окажутся белыми, равна 7/60. Сколько в урне белых шаров?
16. Числа а и б выбираются наугад из промежутка соответственно [0; 8] и [0; 10]. Какова вероятность того, что корень уравнения а∙ х = б больше 1?
17. Вероятность дозвониться с первой попытки в справочное бюро вокзала равна 0.4. Какова вероятность того, что: а) удастся дозвониться при втором звонке;
б) придется звонить не более трёх раз?
18. Из 1000 ламп 590 принадлежат первой партии, 200 – второй, остальные – третьей. В первой партии 6% бракованных ламп, во второй – 5%, в третьей – 4%. Наудачу выбирается лампа. Она оказалась бракованной. Какова вероятность того, что лампа принадлежала первой партии?
19. Вероятность того, что изделие не выдержит испытания, равна 0.004. Какова вероятность того, что из 750 проверяемых изделий более трех изделий не выдержат испытания?
20. В ящике лежат 9 кубиков с номерами от 1 до 9. Найти вероятность того, что появятся кубики: а) с номерами 2, 5, 9; б) с номерами 5, 2, 9, в) с номерами 4, 5, 4.
21. 52 игральные карты раздаются 4 игрокам. Найти вероятность того, что: а) все тузы будут у одного игрока; б) каждый игрок получил один туз.
22. Какова вероятность того, что произведение двух наугад взятых правильных положительных дробей не больше ¼?
23. Вероятность потери письма в почтовом отделении равна 0.03, а телеграммы – 0.01. Отправлено два письма и одна телеграмма. Какова вероятность того, что дойдет: а) только телеграмма; б) хотя бы одно из отправлений?
24. В первой урне 3 белых и 7 чёрных шаров, во второй – 5 белых и 2 чёрных. Из первой урны переложили во вторую два шара, затем из второй урны извлекли один шар. Какова вероятность того, что он белый?
25. Что вероятнее: выиграть у равносильного партнера: а) три партии из четырех или пять из восьми; б) не менее трех партий из четырех или не менее пяти партий из восьми?
26. Из букв А, С, Н, Н, А, А разрезной азбуки составляется наудачу слово, состоящее из 6 букв. Какова вероятность того, что получится слово «АНАНАС»?
27. В ящике 50 годных и 16 дефектных деталей. Сборщик наудачу достает 8 деталей. Найти вероятность того, что среди них: а) нет дефектных; б) три дефектных.
28. Наудачу выбирают два числа из промежутка [0; 1]. Какова вероятность того, что их сумма заключена между ¼ и 1?
29. В электрической цепи вероятности выхода из строя элементов равны соответственно 0.01, 0.02, 0.03, 0.04. Найти вероятность безотказной работы цепи, если элементы 1, 2, 3 соединены параллельно между собой и к ним последовательно подсоединен 4 элемент.
30. Турист вышел на поляну, откуда вело 5 дорог. Известно, что вероятности выхода из леса за час различных дорог равны соответственно: 0.6, 0.3, 0.2, 0.1, 0.1. Через час турист вышел из леса. Чему равна вероятность того, что он пошел по первой дороге?
31. Учебник издан тиражом 100 000 экземпляров. Вероятность неправильной брошюровки учебника равна 0.0001. Найти вероятность того, что тираж содержит ровно 5 бракованных книг.
32. Двое друзей, А и Б, стоят в очереди из 8 человек. Какова вероятность того, что а) А и Б стоят рядом; б) между А и Б стоят два человека?
33. Из 40 вопросов, входящих в экзаменационные билеты, студент знает 30. Найти вероятность того, сто среди трех наугад выбранных вопросов студент знает: а) 3 вопроса: б) 2 вопроса: в) 1 вопрос.
34. Какова вероятность того, что корни уравнения 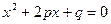 будут действительными, если коэффициенты
будут действительными, если коэффициенты 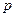 и
и 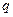 уравнения выбираются наудачу из отрезка [0; 1]?
уравнения выбираются наудачу из отрезка [0; 1]?
35. В электрической цепи вероятности выхода из строя элементов равны соответственно 0.01, 0.02, 0.03, 0.04. Найти вероятность безотказной работы цепи, если параллельно соединенные элементы 1 и 2 соединены последовательно с параллельно соединенными элементами 3 и 4.
36. Система обнаружения самолета из-за наличия помех в зоне действия локатора может давать ложные показания с вероятностью 0.05, а при наличии цели в зоне система обнаруживает ее с вероятностью 0.9. Вероятность появления противника в зоне равна 0.25. Определить вероятность ложной тревоги.
37. Монета подбрасывается 2020 раз. Какова вероятность того, что герб выпадет 1000 раз?
38. На зачетное занятие пришли 20 студентов. Из них 10 подготовлены хорошо, а 10 – слабо. Студенты рассаживаются парами. Какова вероятность того, что каждый слабый студент окажется в одной паре с сильным?
39. В группе 12 юношей и 10 девушек. Для дежурства выделяют 5 человек. Какова вероятность того, что в число дежурных войдут: а) 2 юноши и 3 девушки; б) 4 юноши и 1 девушка?
40. В круг вписан квадрат. Найти вероятность того, что а) точка, брошенная наудачу внутрь круга, окажется и внутри квадрата; б) из пяти точек, брошенных наудачу внутрь круга, одна окажется внутри квадрата и по одной точке попадет на каждый сегмент.
41. В ящике лежат шары трёх цветов: 10 синих, 8 –красных и 7 зеленых. Какова вероятность того, что из трёх извлеченных шаров по крайней мере два окажутся одного цвета?
42. Имеется 1000 лампочек. События, что среди них неисправны 0, 1, 2, 3, 4, 5 лампочек – равновозможные. Из взятых наудачу 100 лампочек все оказались исправными. Какова вероятность того, что среди 1000 лампочек не было ни одной неисправной?
43. Вероятность отказа каждого прибора при испытании равна 0.2. Приборы испытываются независимо друг от друга. Что вероятнее: отказ 10 приборов при испытании 80, или отказ 15 приборов при испытании 120 приборов?
44. Какова вероятность того, что наудачу составленное четырёхзначное число составлено а) из разных цифр; б) только из нечётных цифр?
45. 25 экзаменационных билетов содержат по 2 вопроса. Студент может ответить только на 35 вопросов. Какова вероятность того, что студент вытянет хороший билет?
46. В течение трех часов касса один раз закрывается на перерыв на 15 минут. Клиенту для оформления билета требуется 5 минут. С какой вероятностью клиент будет обслужен без задержки?
47. В электрической цепи вероятности выхода из строя элементов равны соответственно 0.01, 0.02, 0.03, 0.04. Найти вероятность безотказной работы цепи, если последовательно соединены элементы 1, 2 и пара параллельно соединенных элементов 3 и 4.
48. У рыбака имеется три излюбленных места для ловли рыбы, которые он посещает с равной вероятностью каждое. Вероятности поймать рыбу при одном закидывании удочки равны –0.8, 0.6, 0.5 соответственно. Известно, что рыбак, выйдя на ловлю рыбы, три раза закинул удочку и рыба клюнула только один раз. Найти вероятность того, что он удил рыбу на первом месте.
49. Вероятность попадания в цель из орудия при отдельном выстреле равна 0.75. Найти вероятность того, что при 300 выстрелах число попаданий будет не менее 210, но не более 230 раз.
50. В партии из 20 деталей имеется 4 неисправных. Наугад выбираются 3 детали. Какова вероятность, что среди них хотя быодна исправна?
51. Два спортсмена должны выполнить норму мастера спорта. Вероятность того, что первый выполнит норму, равна 0.9, второй – 0.8. Найти вероятность того, что норма будет выполнена а) только одним спортсменом
б) двумя спортсменами.
52. Имеются две урны с шарами по 10 и 8 шаров, причем в каждой урне 1 шар белый. Шар, наугад взятый из первой урны, переложен во вторую, после чего шар, наугад взятый из второй урны, - в первую. Какова вероятность, что состав шаров в урнах не изменится?
53. Как изменится надёжность схемы, изображённой на рисунке, если продублировать /параллельно/ круглое устройство одним, а квадратное – двумя дополнительными? Надёжность круглого устройства 0.9, а квадратного 0.7.

54. Пара одинаковых игральных костей бросается 7 раз. Какова вероятность того, что сумма очков, равная 7, выпадет дважды?
55.Среди 15 книг имеется 5 по математике. Наугад выбираются 4 книги. Какова вероятность, что более двух по математике.
56. Батарея из трёх орудий производит залп по цели. Вероятности попадания в цель первым, вторым и третьим орудием соответственно равны: 0.7, 0.8 и 0.9. Найти вероятность того, что: а) не было ни одного попадания б) хотя бы одно попадание.
57. На двух станках производятся одинаковые детали. Вероятность того, что деталь, произведенная 1-м станком, будет стандартной, равна 0.6, а вторым - 0.9. Производительность второго станка втрое больше производительности первого. Найти вероятность того, что будет стандартной деталь, взятая наугад с транспортера, на который сбрасываются детали с обоих станков.
58. Как изменится надёжность схемы изображённой на рисунке, если продублировать /параллельно/ круглое устройство двумя дополнительными? Надёжность круглого устройства 0.8, а квадратного 0.9.

59. Определить вероятность того, что в семье, имеющей 5 детей, будет 2 девочки и 3 мальчика. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
60. В партии из 12 телевизоров имеются 4 неисправных. Наугад отобраны 3 телевизора. Какова вероятность , что хотя бы один исправный?
61. Баскетболист производит два штрафных броска. Вероятность попадания мяча в корзину при каждом броске равна 0,8. Найти вероятность того, что будет
а) только одно попадание б) два попадания.
62. В вычислительной лаборатории имеется 6 клавишных автоматов и 4 полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не откажет, равна 0.9, а для полуавтомата эта вероятность равна 0.7. Студент производит расчет на наудачу взятой машине. Найти вероятности того, что до окончания расчета машина не откажет.
63. Найти надёжность схем, изображённых на рисунке, если надёжность (вероятность не выхода из строя) i-го устройства равна  .
.

64. Пара одинаковых игральных костей бросается 7 раз. Какова вероятность того, каждый раз выпадет сумма очков, большая 7?
65. В группе 30 студентов. 8 студентов не подготовились к занятию. Наугад вызываются 3 студента. Найти вероятность, что двое подготовились, а третий – нет.
66. В партии 8 деталей, из них 6 стандартных. Найти вероятность того что среди наудачу извлеченных 2 деталей а) хотя бы одна стандартная б) только одна стандартная.
67. В группе спортсменов лыжников в 2 раза больше, чем бегунов, а бегунов в 3 раза больше, чем велосипедистов. Вероятность выполнить норму для лыжника – 0.9, для бегуна – 0.75, для велосипедиста – 0.8. Найти вероятность того, что спортсмен, выбранный наугад, выполнит норму.
68. Пара одинаковых игральных костей бросается 7 раз. Какова вероятность того, что сумма очков, равная 7, выпадет по крайней мере 1 раз?
69. Определять вероятность того, чтo партия из 20 деталей, среди которых 4 бракованных, будет принята при испытании наудачу выбранной половины всей партии изделий.
70. Три стрелка производят по одному выстрелу в мишень. Вероятность попадания в мишень первым стрелком равна 0.9, вторым – 0.8, третьим – 0.7. Найти вероятность того, что мишень будет поражена а) только одним стрелком б) хотя бы одним стрелком.
71. Студент выучил 15 билетов из 20. Какова вероятность вынуть неизвестный билет, если он берет билет вторым?
72. Пара одинаковых игральных костей бросается 7 раз. Какова вероятность того, что ни разу не выпадет сумма очков, равная 12?
73. В коллекции 20 пластинок имеется 5 с произведениями Моцарта. Наугад выбираются 4 пластинки. Какова вероятность того, что хотя бы одна с произведениями Моцарта?
74. Два стрелка произвели по одному выстрелу. Вероятность попадания в мишень первым стрелком равна 0.7, а вторым – 0.6, Найти вероятность того, что будет а) ровно одно попадание б) два попадания.
75. В двух ящиках содержится по 15 деталей, причем из них в первом ящике 9, а во втором 10 стандартных деталей. Из первого ящика наугад извлечена одна деталь и переложена во второй ящик. Найти вероятность того, что наудачу извлеченная после этого деталь из второго ящика будет стандартной.
76. Пара одинаковых игральных костей бросается 5 раз. Какова вероятность того, что ни разу не выпадет сумма очков, меньшая 6?
77. В водоёме имеется 13 крокодилов, из них 5 голодных и 8 сытых. Какова вероятность того, что 3 наугад выбранных крокодила – сытые?
78. Пассажир поезда купил 2 пирожка – один с картошкой и один с мясом. Пирожок с картошкой свежий с вероятностью 0.9, а с мясом – 0.5. Найти вероятность того, что а) оба пирожка свежие б)только один свежий.
79. В гостинице дежурный администратор с вероятностью 0.1 отсутствует у телефона, а с вероятностью 0.7 – спит. Какова вероятность, позвонив 1 раз, переговорить с администратором, если звонок будит его с вероятностью 0.3?
80. Пара одинаковых игральных костей бросается 6 раз. Какова вероятность того, что сумма очков, меньшая 5, выпадет ровно 2 раза?
81. Имеется 15 пирожков, из них 3 с картошкой, а остальные с мясом. Какова вероятность, что из двух наудачу выбранных пирожков один с мясом и один с картошкой?
82. Один из двух приборов исправен с вероятностью 0.7, другой – 0.8. Найти вероятность того, что а) только один прибор исправен б) хотя бы один прибор исправен.
83. Имеются две урны с шарами по 5 и 10 шаров, причем в каждой урне 2 шара чёрных. Шар, наугад взятый из первой урны, переложен во вторую, после чего шар, наугад взятый из второй урны, - в первую. Какова вероятность, что состав шаров в урнах не изменится?
84. Биатлонист попадает в мишень с вероятностью 0.9. Какова вероятность того, что за 5 выстрелов он поразит ровно 3 мишени из имеющихся 5?
85. На складе имеется 15 ящиков с помидорами, из них 5 с зелеными и 10 с красными. Какова вероятность того, что из 4 наугад выбранных ящиков ровно 3 с красными?
86. Пассажир поезда купил 2 пирожка – один с картошкой и один с мясом. Пирожок с картошкой свежий с вероятностью 0.8, а с мясом – 0.2. Найти вероятность того, что будет а) оба пирожка не свежие
б) только один свежий.
87. В первом водоёме имеется 10 сытых крокодилов, во втором – 5 голодных и 4 сытых. Один крокодил переполз из второго водоема в первый, а затем два – из первого во второй. Какова вероятность того, что в первом водоёме все крокодилы по-прежнему сытые?
88. Пара одинаковых игральных костей бросается 6 раз. Какова вероятность того, что сумма очков, большая 10, выпадет ровно 3 раза?
89. Из урны, содержащей 6 белых и 4 чёрных шаров, случайным образом и без возвращения извлекается 4 шара. Случайная величина x – число белых шаров в выборке. Найти ряд распределения случайной величины x, Mx, Dx. Построить график функции распределения случайной величины x. Найти  .
.
90. Стрелок производит несколько выстрелов в цель до первого попадания, имея всего четыре патрона. Вероятность попадания при одном выстреле равна 0,6. Найти ряд распределения случайной величины x, Mx, Dx, где x – число неизрасходованных патронов. Построить график функции распределения случайной величины x. Найти  .
.
91. Устройство содержит 1000 одинаково надежных элементов, каждый из которых может отказывать с вероятностью0,003. Какова вероятность, что откажет: а) более двух элементов, б) хотя бы один элемент?
Найти математическое ожидание и дисперсию случайной величины x - числа отказавших элементов.
92. Случайная величина x подчинена закону распределения с плотностью f(x), причем
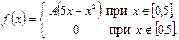 Найти параметр A ,
Найти параметр A , 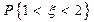 , Mx , Dx .
, Mx , Dx .
Построить график плотности распределения вероятности случайной величины x .
93. Найти параметр А, математическое ожидание и дисперсию случайной величины x плотность вероятности которой
 Найти
Найти 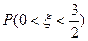 .
.
Построить график плотности распределения вероятности случайной величины x.
94. Известно, что время x безотказной работы радиолампы имеет показательное распределение. Найти математическое ожидание
Мx, если  .
.
Построить график плотности распределения вероятности случайной величины x .
95. Известно, что время x безотказной работы радиолампы имеет показательное распределение. Найти 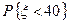 , если Мx = 20.
, если Мx = 20.
Построить график плотности распределения вероятности случайной величины x .
96. Измерительный прибор не имеет систематической ошибки, а средняя квадратичная ошибка равна 75. Какова вероятность, что ошибка измерения не превзойдет по абсолютной величине 45 (закон распределения – нормальный) ?
98. Случайное отклонение длины изделия от стандарта при его изготовлении на данном станке имеет систематическую ошибку 2 мм. Какова вероятность, что длина изделия находится в пределах от 8 до 12 мм, если средняя квадратичная ошибка равна 10 мм, а ошибки распределены по нормальному закону ?
99. Систематическая ошибка высотомера равна нулю, а случайные ошибки распределены по нормальному закону. Какую среднюю квадратичную ошибку должен иметь высотомер, чтобы с вероятностью 0,95 ошибка измерения высоты по абсолютной величине была меньше 50 м ?
100. Каким должен быть допуск отклонения размера детали от номинала, чтобы с вероятностью 0,9 отклонение было допустимым, если систематическая ошибка отклонения отсутствует, а средняя квадратичная равна 25 мм (закон распределения – нормальный)?
101. Деталью высшего качества считается такая, у которой отклонение размера от номинала не превосходит по абсолютной величине 4,3 мк. Случайное отклонение распределено по нормальному закону. Найти среднюю квадратичную ошибку, если систематическая ошибка равна нулю, а вероятность того, что деталь высшего качества равна 0,99.
102. Случайная величина x распределена по закону Коши с плотностью

Найти плотность распределения вероятности случайной величины h. Варианты: 1.  2.
2. 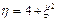
3. 4. 5. 6. 7. 8. 9. .
