Квадрат түбірлер әдісі

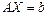сызықтық теңдеулер жүйесі берілсін, мұндағы А симметриялы матрица, яғни .

Тура жүрісі. А матрицасын өзара транспонирленген екі үшбұрышты матрицаларының көбейтіндісі ретінде жазуға болады

, (1)

мұндағы

,

Т матрицасының элементтерін аныктау үшін және Т матрицаларын көбейтіп А матрицасына теңестіреміз.

(2)

(5) қатынас орындалса, (1) теңдеу келесі екі теңдеумен пара-пар

. (3)

Кері жүрісі. (7) теңдеулерді жүйе арқылы жазамыз

және

Осы жүйелерден біртіндеп у және х мәндерін табамыз:

МЫСАЛ.

Сызықтық алгебралық теңдеулер жүйесін квадрат түбірлер әдісімен шешу керек

Шешуі. Тура жүрісі. t_іj элементтерін табамыз

;

Кері жүрісі

1) табамыз

2) табамыз:

Жауабы: .

2. Бір ғана бөлу схемасында тік және кері жүрістің мағынасы неде?

3. Зейдель әдісінің итерациялық процесі қарапайым итерацияның сондай әдісінен қандай өзгешілігі бар?

Бақылау сұрақтары:

1. Квадрат түбірлер әдісін қолдану шарты қандай?
2. Квадрат түбірлер әдісі дәл әдіс пе әлде итерациялық әдіс пе?
3. Квадрат түбірлер әдісінде тура және кері жүрістің мағынасы неде?

Дәріс. Сызықтық алгебралық теңдеулер жүйесiн шешудің итерациялық әдістері. Итерациялық әдістердің жинақталуы. Оптималды параметрлі итерациялық әдістер.