Расчет арок на подвижную нагрузку

Линии влияния опорных реакций

Для определения вида линии влияния реакции R_А составим следующее уравнение равновесия Sm_B = 0,

R_А∙l – P(l – x) = 0.

Тогда линия влияния левой реакции

л. в. R_А = 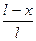. (3.6)

Выражение для линии влияния реакцию R_В определим из уравнения Sm_A = 0,

R_В∙l – P∙ x = 0.

В результате:

л. в. R_В = 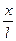. (3.7)

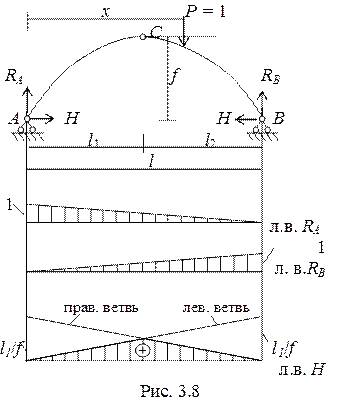
Линии влияния реакций R_А и R_В показаны на рис. 3.8.

Отметим, что линии влияния вертикальных реакций в арке те же, что и в однопролетной балке и в ферме.

Поскольку выражение горизонтальной реакции (распора) связано со значением балочного изгибающего момента в точке С 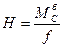, его линия влияния будет иметь две ветви.

Сила Р = 1 справа от точки С. Рассмотрим равновесие левой части арки.

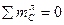, R_А∙l₁ – H∙f = 0. Откуда

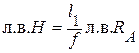. (3.8)

Получили уравнение правой ветви линии влияния H.

Аналогично получим уравнение левой ветви - сила Р = 1 слева от точки С. 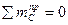, R_В∙l₂ - H∙f = 0. Тогда

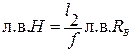. (3.8)′

Линия влияния Н показана на рис. (3.8).

Построение линии влияния изгибающего момента

Воспользуемся выражением для изгибающего момента в арке

M_к = M_к^б – Н∙у_к.

Очевидно, что справедливо следующее утверждение

л.в. M_к = л.в. M_к^б – (л.в.Н)у_к,

то есть линию влияния момента в арке можно построить методом наложения двух линий влияния - M_к^б и Н∙у_к. Поступаем следующим образом.

1. Вверх от оси строим линию влияния M_к^б (на рис. 3.9 показана сплошной линией).

2. На той же оси откладываем ординаты линии влияния Н, умноженные на координату точки «к» у_к (пунктирная линия). Для этого достаточно построить левую ветвь линии влияния Н, умножив ее ординаты на у_к, Правая ветвь будет представлена прямой, соединяющей конец левой ветви (проекция т. С) с нулевой точкой на правой опорной вертикали (проекция т. В).

3. В результате получаем разность ординат линий влияния M_к^б и Н∙у_к (заштрихованная область на рис. 3.9 и представляет собой линию влияния M_к).

Точка F′ – нулевая точка линии влияния M_к.

Положение нулевой точки F′ можно найти графическим построением на чертеже арки (графически). Нулевое значение M_к получается при положении единичной силы в интервале между сечением к и ключевым шарниром С. Так как единичная сила приложена к левому диску арка, линия действия правой реакции В должна проходить через центр ключевого шарнира, поскольку .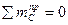

Поскольку единичная сила правее сечения «к», то для выполнения условия, что M_к = 0, реакция А должна действовать по линии Ак. Проводим линии Ак и ВС, под точкой пересечения которых и находится нулевая точка F′.

Для построения линии влияния M_к способом нулевой точки откладываем на левой опорной вертикали ординату 1∙а_к, далее соединяем ее с нулевой точкой F′ - получаем 1-ю правую ветвь. Проводя вертикаль через шарнир С получаем границу 1-й и 2-й правых ветвей (то есть правая ветвь представляет собой ломаную линию).

Левую ветвь находим по 1-й правой ветви, соединяя ее начало с левой опорной точкой.

Ординату нулевой точки можно определить аналитически. Она равна (без вывода)

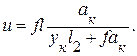(3.9)

Построение линии влияния поперечной силы.

Воспользуемся выражением (3.3) для поперечной силы в арке

Q_к = Q_к^б cosj_к– Н sinj_к. (3.3)

Поскольку для заданного сечения величины cosj_к и sinj_к постоянны, справедливо следующее утверждение

л.в. Q_к = (л.в. Q_к^б )cosj_к – (л.в.Н) sinj_к.

То есть для построения линию влияния поперечной силы в арке можно воспользоваться методом наложения линий влияния Q_к^б и Н, умноженных на значения соответствующих тригонометрических функций. Поступаем следующим образом (рис. 3.10).

1. Строим линию влияния Q_к^бcosj_к для сечения «к».

2. Вверх от оси откладываем ординаты линии влияния Н sinj_к, которые получаем по левой ветви, ордината которой на правой опоре равна (l₂/f) sinj_к.

3. Отмечаем (штрихуем) ординаты, соответствующие выражению (3.3).

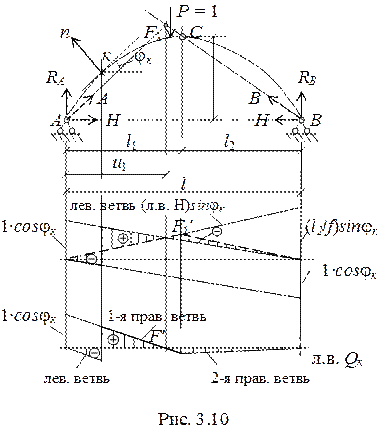Отметим, что в пересечении левой ветви л. в. Н sinj_к с правой ветвью л. в. Q_к^бcosj_к находится нулевая точка F₁′, положение которой можно установить графически по чертежу арки. Действительно, если сила Р = 1 находится между точками к и С, то слева от точки «к» будет действовать только реакция А и для того, чтобы в сечении «к» выполнялось условие 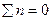, реакция должна быть параллельна касательной к оси арки в сечении «к».

В то же время, линия действия реакции В будет направлена вдоль прямой ВС. На пересечении этих прямых находится нулевая точка F₁.

Для построения линии влияния поперечной силы в арке методом нулевой точки достаточно в сечении «к» провести касательную к оси арки направить реакцию А по этой касательной до пересечения с прямой , соединяющей шарниры С и В и получить положение нулевой точки. Далее, отложить на левой опорной вертикали ординату cosj_к и провести 1-ю правую ветвь через точку F₁′. Проводя вертикаль через шарнир С получаем границу 1-й и 2-й правых ветвей. Затем проводим левую ветвь, которая параллельна 1-й правой ветви (рис. 3.10).

Положение нулевой точки F₁ можно определить аналитически

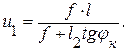(3.10)

Построение линии влияния продольной силы.

По аналогии с построением линии влияния поперечной силы, для построения линии влияния продольной силы можно применить метод наложения и метод нулевой точки.

Для метода наложения необходимо воспользоваться выражением для продольной силы в арке

N_к = – Q_к^б sinj_к – Н cosj_к, (3.4)

тогда:

л.в. N_к = (л.в. Q_к^б )sinj_к + (л.в.Н) cosj_к.

Здесь мы учли, что сжимающая сила в арке считается положительной.

Воспользуемся методом наложения (рис. 3.11).

1. Строим линию влияния Q_к^б sinj_к.

2. От оси вниз строим линию влияния Н cosj_к по левой ветви (пунктирная линия).

3. Складываем ординаты построенных линий влияния.

Если продолжить правую ветвь (л.в.Н) cosj_к и левую ветвь (л.в. Q_к^б ) sinj_к получим точку F₂′. Если предположить наличие консоли – ответвления от участка арки кС, по которой перемещается единичная сила, то слева отсечения «к» действует только реакция А. Если она направлена вдоль оси n, то N_к = 0, т. е.

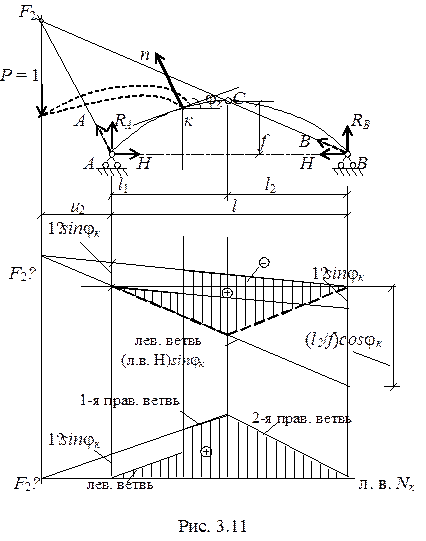
нулевая точка находится на пересечении прямых ВС и линии действия реакции А.

Для построения лини влияния N_к методом нулевой точки достаточно найти положение т. F₂′, затем отложить от левой опоры ординату sinj_к и соединить полученные точки до координаты шарнира С – получим 1-ю правую ветвь. Далее строим 2-ю правую ветвь, проводя прямую от конца 1-й правой ветви до правой опоры. Левая ветвь параллельна 1-й правой ветви.

Координата нулевой точки равна

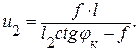(3.11)

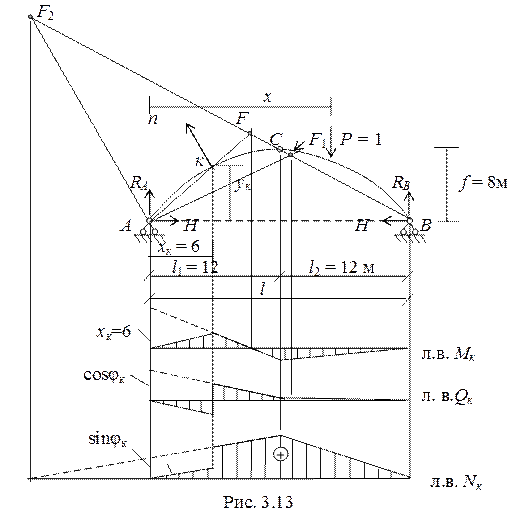
Пример 3.3.Построить линии влияния опорных реакций и внутренних усилий в сечении «к» для арки параболического очертания. Размеры арки указаны на чертеже.

Решение. Построение линий влияния опорных реакций R_A, R_B и распора H однотипно для трехшарнирных систем, так как не зависит от очертания арки (рис. 3.12).

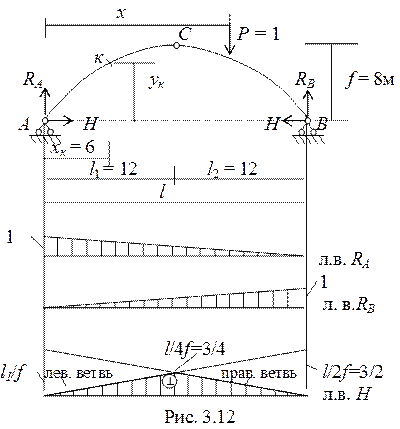
Для построения линий влияния внутренних усилий вычислим координаты сечения «к» и тригонометрические функции угла φ_к.

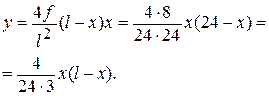
y_k =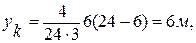

φ_k = 33,6°, sinφ_k = 0.554, cosφ_k = 0.836.

Построение указанных линий влияния проведем методом нулевой точки (рис. 3.13).

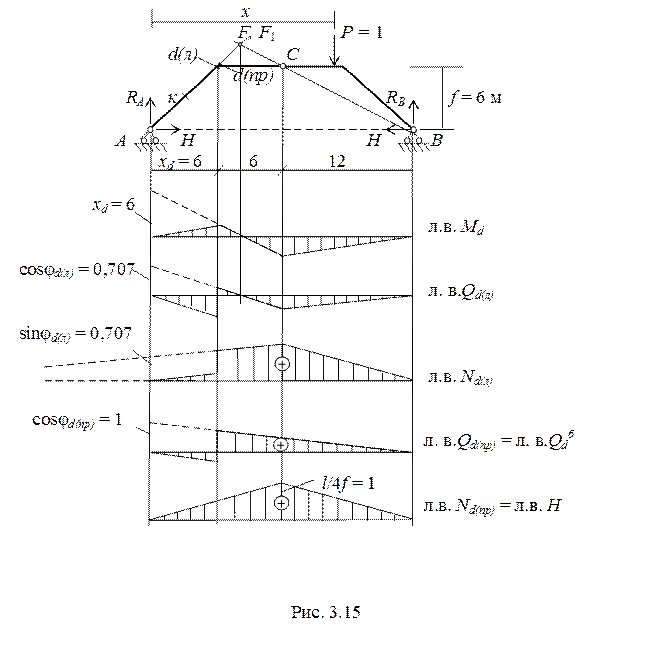
Пример 3.4.Построить линии влияния внутренних усилий в сечениях «к» и «д» в трехшарнирной раме. Размеры рамы указаны на чертеже (рис. 3.14).

Для построения линий влияния внутренних усилий вычислим координаты сечений «к» и «d» и тригонометрические функции углов φ_к и φ_d.

x_k = 3 м, x_d = 6 м.

φ_k = 45°, sinφ_k = 0.707, cosφ_k = 0.707,.

φ_d(л) = 45°, sinφ_d(л) = 0.707, cosφ_d(л) = 0.707.

φ_d(пр) = 0°, sinφ_d(пр) = 0, cosφ_d(пр) = 1.

Построение указанных линий влияния проводим методом нулевой точки (рис. 3.14, 3.15). Линии влияния Q_d(пр) и N_d(пр) построены методом наложения.