Расчет показателей надежности систем с восстановлениями при произвольных законах распределения времени безотказной работы и восстановления

Предыдущий метод расчета показателя надежности базируется на экспоненциальных законах распределения безотказной работы и восстановления. Он называется методом «переходных интенсивностей», потому что интенсивности – константы (экспоненциальный закон).

Для произвольных законов распределения используется метод переходных вероятностей.

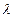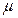Уже нет требования к постоянству и , что соответствует нестационарной системе.

Идея метода.

Так же как в методе переходных интенсивностей ( 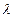, 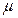- константы) используется граф переходов.

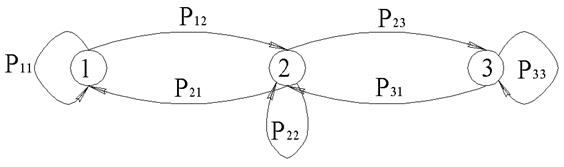
Рис. 12 Граф.

Здесь указываются вероятности переходов из одного состояния в другое.

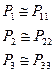
Вероятности записываются в виде матрицы .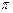

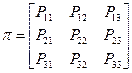
Первая строка соответствует вероятности перехода из 1-го состояния и т.д.

Для схемы (рис. 12.)

.

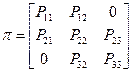Сумма по строке должна быть равна единице.

Если рассмотреть изменение состояния по этапам и ввести гипотезу (допущение) о независимости вероятностей и переходов от предыдущих состояний.

Неважно, как попало состояние, далее движение происходит независимо.

Так же система при стационарности интенсивности перепадов называется Марковскими цепями.

В данном случае веса дуг меняются во времени, т.е. интенсивность изменяется, поэтому такой граф называется Марковским (цепь полумарковская).

С учетом этого предположения на каком такте для 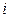-й вероятности можно записать:

.

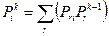Произведение отражает, что два события независимы.

Совпадение двух событий (независимых) отражается произведением.

Таким образом, для данного графа:

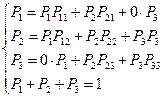(3.3)

Все вероятности зависят от времени.

Одно из уравнений не принимается к расчету.

Поскольку система нестационарная, аналитических методов получения зависимости 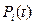не существует.

Численный метод:

1) Задаются начальные условия;

2) Задается шаг квантования по времени. Шаг квантования выбирается обычно из

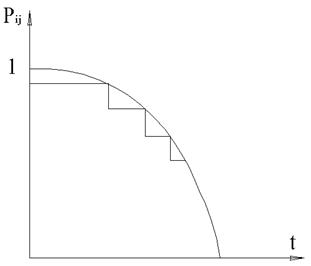
Рис. 13. Ступеньки.

Т.е. по среднему значению ступенек, которое мало отличается от крайних значений (порядка 200 часов).

3) Итеративно (по точкам) начинают решать систему уравнений

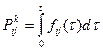(3.4)

при этом кривая должна быть задана.

Решение заканчивается тогда, когда вероятности перестают изменяться, т.е. заканчивается переходный процесс.

Пример 4.

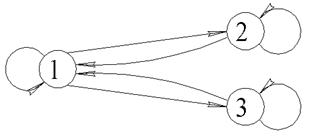
Рис. 14. Граф.

Матрица 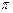запишется в виде:

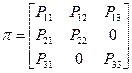
система уравнений

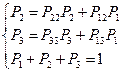
начальные условия: ; ;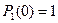

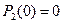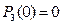
берем интервал времени 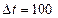часов.

1) Шаг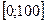

На этом интервале

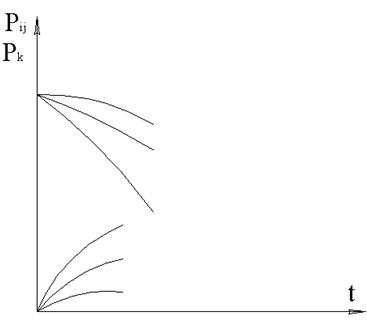
Рис. 15. Кривые изменения вероятностей.

Понятно, что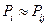

Допустим, что вероятность

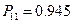
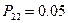
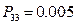
при .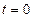

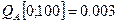
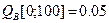
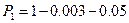
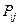- рассчитывается.

Полученные вероятности подставляются в систему уравнений и решают ее.

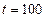часов

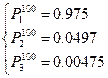
2) Вычислим 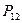и т.д. исходя из того, что нам задано.

3) Получаются новые решения.

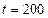
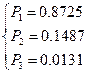
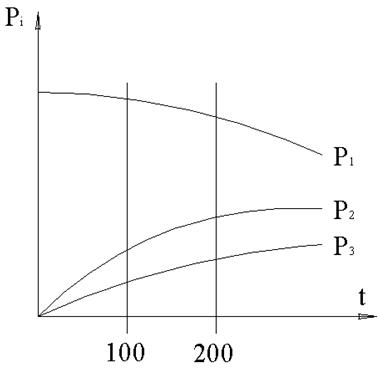
Рис. 16. Вероятность.

Предельное (финальное) значение вероятностей находятся по этой же системе, но беда в том, что финальное значение 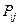неизвестно, поэтому могут быть получены только оценки.

Пример 5

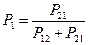- для системы, имеющей два состояния.

Рис. 17. Система с двумя состояниями

4. Достоинства и недостатки «дерева событий»

Анализ причин промышленных аварий показывает, что возникновение и развитие крупных аварий, как правило, характеризуется комбинацией случайных локальных событий, возникающих с различной частотой на разных стадиях аварии (отказы оборудования, человеческие ошибки при эксплуатации/проектировании, внешние воздействия, разрушение/разгерме-тизация, выброс/утечка, пролив вещества, испарение, рассеяние веществ, воспламенение, взрыв, интоксикация и т.д.). Для выявления причинно-следственных связей между этими событиями используют логико-графические методы деревьев отказов и событий. Модели процессов в человеко-машинных системах должны отражать процесс появления отдельных предпосылок и развития их в причинную цепь происшествия в виде соответствующих диаграмм причинно-следственных связей – диаграмм влияния. Такие диаграммы являются формализованными представлениями моделируемых объектов, процессов, целей, свойств в виде множества графических символов (узлов, вершин) и отношений – предполагаемых или реальных связей между ними. Широкое распространение получили диаграммы в форме потоковых графов (графов состояний и переходов), деревьев событий (целей, свойств) и функциональных сетей различного предназначения и структуры.

Основные достоинства: сравнительная простота построения; дедуктивный характер выявления причинно-следственных связей исследуемых явлений; направленность на их существенные факторы; легкость преобразования таких моделей; наглядность реакции изучаемой системы на изменение структуры; декомпозируемость «дерева» и процесса его изучения; возможность качественного анализа исследуемых процессов; легкость дальнейшей формализации и алгоритмизации; приспособленность к обработке на средствах ВТ; доступность для статистического моделирования и количественной оценки изучаемых явлений, процессов и их свойств.

Создание дерева заключается в определении его структуры: а) элементов – головного события (происшествия) и ему предшествующих предпосылок; б) связей между ними – логических условий, соблюдение которых необходимо и достаточно для его возникновения.

На практике обычно используют обратную или прямую последовательность выявления условий возникновения конкретных происшествий или аварийности и травматизма в целом: а) от головного события дедуктивно к отдельным предпосылкам, либо б) от отдельных предпосылок индуктивно к головному событию.

Из анализа структуры диаграммы влияния следует, что основными ее компонентами служат узлы (вершины) и связи (отношения) между ними. В качестве узлов обычно подразумеваются простейшие элементы моделируемых категорий (переменные или константы) – события, состояния, свойства, а в качестве связей – активности, работы, ресурсы и другие взаимодействия. Отношения или связи между переменными или константами в узлах диаграммы графически представляются в виде линий, называемых дугами или ребрами.

Каждые два соединенных между собой узла образуют ветвь диаграммы. В тех случаях, когда узлы связаны направленными дугами таким образом, что каждый из них является общим ровно для двух ветвей, возникают циклы или петли. Переменные в узлах характеризуются фреймами данных – множеством выходов (значений, принимаемых переменными, неизменных во времени и между собой не пересекающихся) и условными распределениями вероятностей появления каждого из них.

Идея прогнозирования размеров ущерба от происшествий в человеко-машинных системах основана на использовании деревьев специального типа (деревьев исходов) – вероятностных графов. Их построение позволяет учитывать различные варианты разрушительного воздействия потоков энергии или вредного вещества, высвободившихся в результате происшествия.

С помощью предварительно построенных диаграмм – графов, сетей, и деревьев могут быть получены математические модели аварийности и травматизма.

В исследовании безопасности широкое распространение получили диаграммы влияния ветвящейся структуры, называемые «деревом» событий (отказов, происшествий). Деревом событий называют не ориентированный граф, не имеющий циклов, являющийся конечным и связным. В нем каждая пара вершин должна быть связанной (соединенной цепью), однако все соединения не должны образовывать петель (циклов), т.е. содержать такие маршруты, вершины которых одновременно являются началом одних и концом других цепей.

Структура дерева происшествий обычно включает одно, размещаемое сверху нежелательное событие – происшествие (авария, несчастный случай, катастрофа), которое соединяется с набором соответствующих событий – предпосылок (ошибок, отказов, неблагоприятных внешних воздействий), образующих определенные их цепи или «ветви». «Листьями» на ветвях дерева происшествий служат предпосылки – инициаторы причинных цепей, рассматриваемые как постулируемые исходные события, дальнейшая детализация которых не целесообразна. В качестве узлов дерева происшествий могут использоваться как отдельные события или состояния, так и логические условия их объединения (сложения или перемножения).

Данный метод, как и любой другой, обладает определенными достоинствами и недостатками. Так, например, метод дает представление о поведении системы, но требует от специалистов по надежности глубокого понимания системы и конкретного рассмотрения каждый раз только одного определенного отказа; помогает дедуктивно выявлять отказы; дает конструкторам, пользователям и руководителям возможность наглядного обоснования конструктивных изменений и анализа компромиссных решений; позволяет выполнять количественный и качественный анализ надежности; облегчает анализ надежности сложных систем.

Вместе с тем реализация метода требует значительных затрат средств и времени. Кроме того, полученные результаты трудно проверить и трудно учесть состояния частичного отказа элементов, поскольку при использовании метода, как правило, считают, что система находится либо в исправном состоянии, либо в состоянии отказа. Существенные трудности возникают и при получении в общем случае аналитического решения для деревьев, содержащих резервные узлы и восстанавливаемые узлы с приоритетами, не говоря уже о тех значительных усилиях, которые требуются для охвата всех видов множественных отказов.

Практическая часть

Задача 1

В результате наблюдений за 45 образцами радиоэлектронного оборудования получены данные до первого отказа всех 45 образцов. Определить: Р(t); α(t); λ(t) в функции времени, построить графики этих функций, а также найти среднюю наработку до первого отказа (T_ср).

Δti,ч	n(Δti)	Δti,ч	n(Δti)
0-5		40-45
5-10		45-50
10-15		50-55
15-20		55-60
20-25		60-65
25-30		65-70
30-35		70-75
35-40		75-80

Дано: Решение:

N₀= 45 Определим вероятность безотказной работы по формуле:

Δt= 5ч Р(t)= ;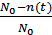

Р(t) -? Р(5) = 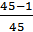= 0,98; Р(10) = 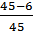= 0,87; Р(15) = 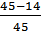= 0,69;

α(t) -? Р(20) = 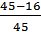= 0,64; Р(25) = 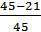= 0,53; Р(30) = 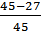= 0,4;

λ(t) -? Р(35) = 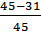= 0,31; Р(40) = 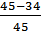= 0,24; Р(45) = 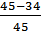= 0.24;

Т_ср -? Р(50) = 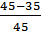= 0,22; Р(55) = 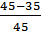= 0.22; Р(60) = 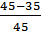= 0.22;

Р(65) = 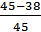= 0,16; Р(70) = 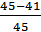= 0,09; Р(75) = 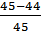= 0,02;

Р(8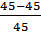0) = =0.

Найдем частоту отказов по формуле: α(t)=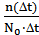

α(2,5)= 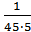= 0,44·10^-2; α(7,5)= 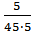= 2,22·10^-2; α(12,5)= 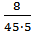= 3,55·10^-2;

α(17,5)= 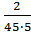= 0,88·10^-2; α(22,5)= 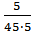= 2,22·10^-2; α(27,5)= 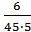= 2,66·10^-2;

α(32,5)= 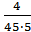= 1,77·10^-2; α(37,5)= 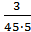= 1,33·10^-2; α(42,5)= 0;

α(47,5)= 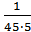= 0,44·10^-2; α(52,5)= 0; α(57,5)= 0; α(62,5)= 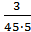= 1,33·10^-2;

α(67,5)= 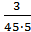= 1,33·10^-2; α(72,5)= 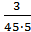= 1,33·10^-2; α(77,5)= 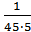= 0,44·10^-2.

Найдем интенсивность отказов по формуле: λ(t) =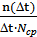

λ(2,5) = 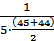= 0,45·10^-2; λ(7,5) = 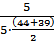= 2,40·10^-3; λ(12,5) = 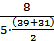= 4,57·10^-3;

λ(17,5) = 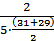=1,33·10^-2; λ(22,5) = 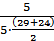=3,77·10^-2; λ(27,5) = 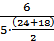=5,71·10^-2;

λ(32,5) = 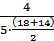= 5·10^-2; λ(37,5) = 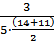= 4,8·10^-2; λ(42,5) = 0;

λ(47,5) = 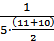= 1,90·10^-2; λ(52,5) = 0; λ(57,5) = 0; λ(62,5) = 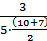=7,05·10^-2;

λ(67,5) = 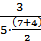= 10,9·10^-2; λ(72,5) = 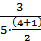= 24·10^-2; λ(77,5) = 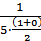= 40·10^-2.

Значения Р(t), α(t), λ(t), вычисленные для всех Δt_i.

Δti,ч	Р(t)	α(t),·10-2ч	λ(t),·10-2ч
0-5	0,98	0,44	0,45
5-10	0,87	2,22	2,40
10-15	0,69	3,55	4,57
15-20	0,64	0,88	1,33
20-25	0,53	2,22	3,77
25-30	0,4	2,66	5,71
30-35	0,31	1,77
35-40	0,24	1,33	4,8
40-45	0,24
45-50	0,22	0,44	1,90
50-55	0,22
55-60	0,22
60-65	0,16	1,33	7,05
65-70	0,09	1,33	10,9
70-75	0,02	1,33
75-80		0,44

Находим среднюю наработку до первого отказа.

Учитывая, что в данном случае: m=t_k/Δt=80/5=16; N₀=45;

имеем:

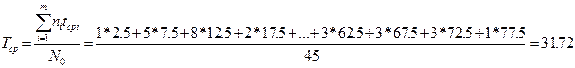
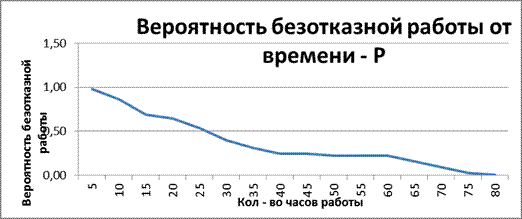
Вероятность безотказной работы на всем процессе наблюдения уменьшается, а в промежутке наблюдения от 40 до 60 часов работы остановилась на уровне 0,22.

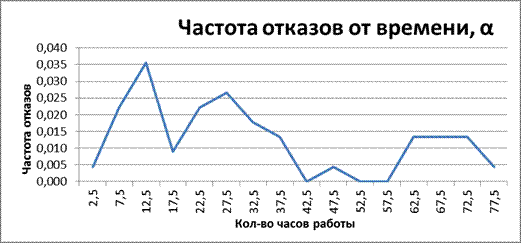
В промежутке времени от 2,5 до 12,5 часов работы частота отказов увеличивалась и достигла 36 * 10^-3 ч. В промежутке от 12,5 до 17,5 часов частота отказов уменьшилась до 9 * 10^-3 ч. В промежутке от 17,5 до 27,5 часов частота отказов увеличилась до 27 * 10^-3 ч. В промежутке от 27,5 до 42,5 часов падает до нуля. В промежутке от 42,5 до 57,5 ч частота отказов не превышает 5*10^-3 ч и после 47,5 часов работы падает до нуля. В промежутке от 57,5 до 62,5 часов работы частота отказов увеличилась до 13 * 10^-3 ч и держалась до 72,5 часов работы наблюдений. В конце испытания частота отказов упала до 4*10^-3ч.

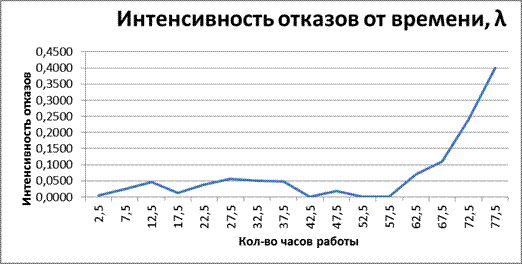
В процессе наблюдения от 2,5 до 57,5 часов интенсивность отказов была в пределах от 0 до 5,71*10^-2 ч. После 57,5 часов работы наблюдений интенсивность отказов резко увеличилась и в конце наблюдения достигла 0,4ч.

Задача №2

В результате наблюдений за 45 образцами радиоэлектронного оборудования, которые прошли предварительную 80-часовую приработку, получены данные до первого отказа всех 45 образцов. Требуется определить : Р(t); α(t); λ(t) в функции времени, построить графики этих функций, а также найти среднюю наработку до первого отказа (T_ср).

Δti, ч	n(Δti)
0 – 10
10 – 20
20 – 30
30 – 40
40 – 50
50 – 60
60 – 70

Решение:

Вычислим Р(t) по формуле:

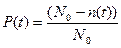
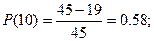
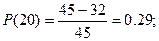
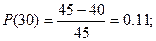
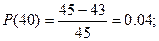
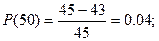
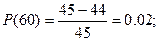
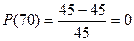
Рассчитываем частоту отказов по формуле:

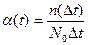
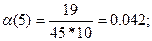
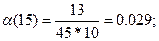
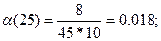
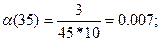
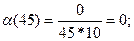
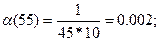
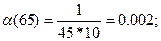
Рассчитываем интенсивность отказов по формуле:

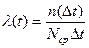
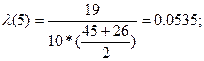
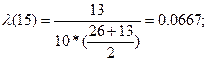
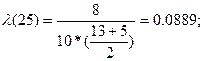
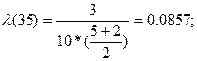
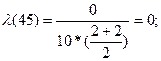
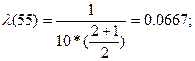
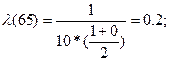
Значения P(t), α(t), λ(t), вычисленные для всех Δt_i сведем в таблицу:

Δti, ч	P(t)	α(t), ч	λ(t), ч
0 – 10	0,58	0,042	0,0535
10 – 20	0,29	0,029	0,0667
20 – 30	0,11	0,018	0,0889
30 – 40	0,04	0,007	0,0857
40 – 50	0,04
50 – 60	0,02	0,002	0,0667
60 – 70		0,002	0,2

Находим среднюю наработку до первого отказа.

Учитывая, что в данном случае: m=t_k/Δt=70/10=7; N₀=45;

имеем:

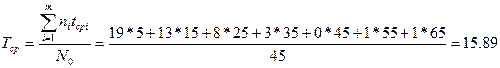
Строим графики функций.

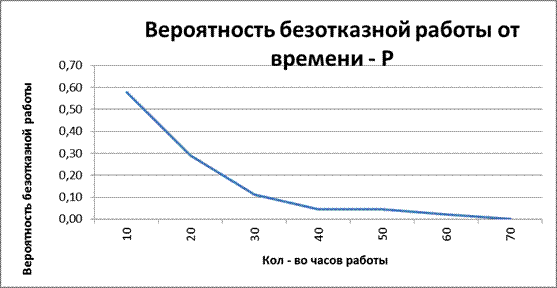
Вероятность безотказной работы радиоэлектронного оборудования падала на всем процессе наблюдений и изменялась от 0,58 до 0.

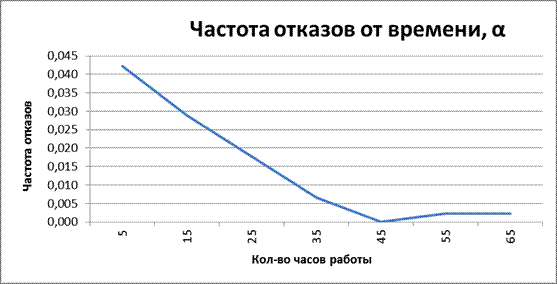
Частота отказов после 5 часов работы радиоэлектронного оборудования составила 4,2*10^-2 ч. Далее частота отказов падала и после 45 часов работы частота достигла нуля. Далее до конца наблюдения частота отказов держалась на отметке 2*10^-3 ч.

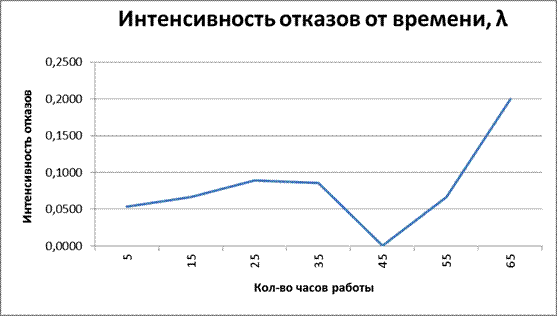
Интенсивность отказов в промежутке времени до 25 часов работы радиоэлектронного оборудования увеличивалась от 53,5 * 10^-3 ч до 88,9 * 10^-3 ч. Далее интенсивность отказов падала и на отметке 45 часов достигла нуля. Потом интенсивность резко увеличилась и в конце наблюдения составила 0,2ч.

Заключение

В ходе проделанной работы:

- изучена методология исследования надёжности технических систем;

- произведена сравнительная оценка эффективности «дерева событий»;

- выполнены все необходимые расчеты, решены поставленные задачи.

Изученный мною материал позволил сделать вывод о том, что большое разнообразие методов оценки надёжности технических систем является явлением необходимым, в силу большого количества задач поставленных перед дисциплиной «надёжность технических систем и техногенный риск». Выявление лучшего метода расчёта надёжности – задача невыполнимая, так как каждый метод применим лишь к определённому спектру задач.

Список используемой литературы

1. Дружинин В.Г. Надёжность автоматизированных систем. «Энергия» 1977. 536 с.

2. Костерев В.В. Надёжность технических систем и управление риском: учебное пособие. – М.: МИФИ, 2008 – 280 с.

3. Сарвин А.А., Абакулина Л.И., Готшальк О.А. Диагностика и надёжность автоматизированных систем: Письменные лекции. – СПб.: СЗТУ, 2003. – 69 с.

4. Рыжкин А.А., Слюсарь Б.Н., Шучев К.Г. Основы теории надёжности: Учеб. Пособие. – Ростов н/Д: Издательский центр ДГТУ. 2002. – 182с.

5. Бобров В.И. Надёжность технических систем: Учеб. Пособие/В.И. Бобров. Моск. гос. Ун-т печати. – М.:МГУП,2004. _236 с.