Проверка истинности параметров уравнения множественной линейной регрессии. Определение стандартных отклонений и t-статистики коэффициентов

Метод наименьших квадратов(МНК, англ. Ordinary Least Squares, OLS) является одним из основных методов определения параметров регрессионных уравнений, Он заключается в том, чтобы определить вид кривой, характер которой в наибольшей степени соответствует выраженной эмпирическими данными зависимости. Такая кривая должна обеспечить наименьшее значение суммы квадратов отклонений эмпирических значений величин показателя от значений, вычисленных согласно уравнению этой кривой. Меняя вид теоретических кривых, приближенно отображающих динамику рассматриваемого показателя, пытаются добиться как можно меньшего значения этой разности.

Для всех моделей проверка качества и статистической значимости опр-ся аналогично моделям парной регрессии.

В Excel считаем R² и F

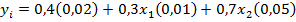
0,02; 0,01; 0,05 – стандартные ошибки

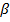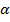0,7	0,3	0,4
0,05	0,01	0,02

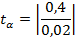
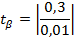
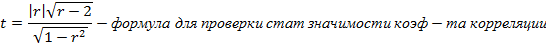
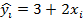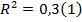		СО(а) = 0,01
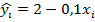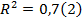		СО(b) = 0,3

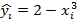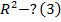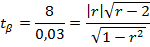Для парной модели t-статистика высчитывается по коэф-ту регрессии b.

Качество модели регрессии связывают с адекватностью модели наблюдаемым (эмпирическим) данным. Проверка адекватности (или соответствия) модели регрессии наблю­даемым данным проводится на основе анализа остатков - .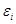

Анализ остатков позволяет получить представление, насколько хорошо подобрана сама модель и насколько правильно выбран метод оценки коэффициентов. Согласно общим предположениям регрессионного анализа, остатки должны вести себя как независимые (в действительности, почти независимые) одинаково распределенные случайные величины.

Качество модели регрессии оценивается по следующим направлениям:

1) проверка качества всего уравнения регрессии;

2) проверка значимости всего уравнения регрессии;

3) проверка статистической значимости коэффициентов уравнения регрессии;

4) проверка выполнения предпосылок МНК.

При анализе качества модели регрессии, в первую очередь, используется коэффициент детерминации, который определяется следующим образом:

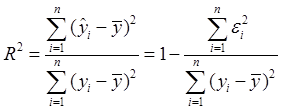, (2.5)

где 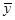- среднее значение зависимой переменной,

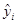- предсказанное (расчетное) значение зависимой переменной.

Коэффициент детерминациипоказывает долю вариации результативного признака, находя­щегося под воздействием изучаемых факторов, т. е. определяет, ка­кая доля вариации признака Y учтена в модели и обусловлена влия­нием на него факторов.

Чем ближе 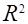к 1, тем выше качество модели.

Для оценки качества регрессионных моделей целесообразно также ис­пользовать коэффициент множественной корреляции (индекс корреляции) R

R = 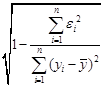= 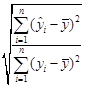(2.6)

Данный коэффициент является универсальным, так как он отра­жает тесноту связи и точность модели, а также может использовать­ся при любой форме связи переменных.

Важным моментом является проверка значимости построенного уравнения в целом и отдельных параметров.

Оценить значимость уравнения регрессии – это означает установить, соответствует ли математическая модель, выражающая зависимость между Y и Х, фактическим данным и достаточно ли включенных в уравнение объясняющих переменных Х для описания зависимой переменной Y

Оценка значимости уравнения регрессии производится для того, чтобы узнать, пригодно уравнение регрессии для практического использования (например, для прогноза) или нет.

Для проверки значимости модели регрессии используется F-критерий Фишера. Если расчетное значение с n₁= k и n₂ = (n - k - 1) степенями свободы, где k – количество факторов, включенных в модель, больше табличного при заданном уровне значимости, то модель считается значимой.

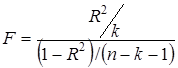(2.7)

В качестве меры точности применяют несмещенную оценку дис­персии остаточной компоненты, которая представляет собой отно­шение суммы квадратов уровней остаточной компоненты к величи­не (n- k -1), где k – количество факторов, включенных в модель. Квадратный корень из этой величины ( 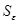) называется стандартной ошибкой:

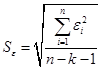(2.8)

значимость отдельных коэффициентов регрессии проверяется по t-статистике пу­тем проверки гипотезы о равенстве нулю j-го параметра уравнения (кроме свободного члена):

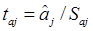, (2.9)

где S_aj— это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии a_j.Величина S_aj представляет собой квадратный корень из произ­ведения несмещенной оценки дисперсии 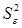и j -го диагонального эле­мента матрицы, обратной матрице системы нормальных уравнений.

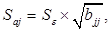
где 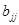- диагональный элемент матрицы .

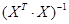Если расчетное значение t-критерия с (n - k - 1) степенями сво­боды превосходит его табличное значение при заданном уровне зна­чимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует ис­ключить из модели (при этом ее качество не ухудшится).