Изучение движения тел в вязкой среде»

Цель работы:на примере движения тела шарообразной формы изучить основные закономерности движения в вязкой среде.

Литература

1. Савельев И.В. Курс общей физики, т.1. Механика и молекулярная физи­ка.

2. Стрелков С.П. Механика.

3. Александров Н.В., Яшкин А.Я. Курс общей физики. Механика.

4. Архангельский М.М. Курс физики. Механика.

Вопросы для допуска к работы

а) знать следующие теоретические вопросы:

1. Понятие пограничного слоя. Чем определяется толщина пограничного слоя? Ламинарное и турбулентное движение.

2. Силы, действующие на тело при его движении в вязкой среде. Определяющие формулы сил, которые действуют на тело.

3. Уравнение движения тела. Характер движения тела на отдельных уча­стках.

4. Число Рейнольдса: его физический смысл и определяющая формула.

б) иметь в протоколе следующие расчетные формулы:

1. Формулу для расчета скорости движения шарика при условии равномерного движения.

2. Формулу, по которой можно оценить число Рейнольдса, зная геометри­ческие размеры, массу шарика и характеристики среды.

3. Формулы для расчета объема тел и площади "миделя".

4. Формулы для оценки погрешности.

Р.S. В расчетные формулы должны входить только те величины, которые могут быть измерены в процессе выполнения работы.

Краткая теория вопроса

На тело, движущееся в вязкой среде, действует сила сопротивления, величина которой зависит от размеров и формы тела, скорости его движения относительно среды и свойств самой среды. Как показал Л. Прандтль, процессы, обуславливающие появление силы сопротивления, в значительной мере определяются явлениями, происходя­щими в пограничном слое и характером вихрей. Вычисление силы сопротивления яв­ляется исключительно сложной задачей и можно лишь оценить порядок этой силы.

В общем случае полная сила сопротивления движению тела в вязкой среде складывается из двух компонент: сопротивления трения и сопротивления давления. Первое слагаемое определяется силами внутреннего трения, возникающим за счет градиента скорости в пограничном слое, второе - разностью давлений на передней и задней кром­ках обтекаемого тела и связано с турбулентным (вихревым) движением жидкости.

Стокс установил, что при небольших скоростях и размерах тел модуль силы сопротивления трения определяется формулой:

F_тр = khLV (1)

где h - динамическая вязкость среды, V - скорость движения тела, L - характерный размер тела и k - коэффициент пропорциональности, который зависит от формы тела. Для шара k = 6p. Исходя из формулы (1) выражение для определения модуля силы сопро­тивления трения имеет вид:

F_тр = 6phR_шV (2)

Модуль силы сопротивления давления определяется формулой:

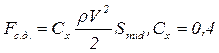(3)

где r - плотность среды, V - скорость движения тела, C_x - характеристический коэффициент обтекаемости тела, зависящий от формы тела, S_mid - площадь "миделя", под кото­рой понимают наибольшую площадь сечения тела плоскостью, перпендикулярной к потоку.

Для оценки вклада той или иной силы в величину полной силы сопротивления движению в вязкой среде введено число Рейнольдса Re, которое определяется как отношение силы сопротивления давления к силе трения. Так при Re£0,5 (ламинарное движение) учитывают только силу сопротивления трения. При 0,5<Re£1 - учитывают

обе компоненты, а при Re>1, т.е. турбулентных (вихревых) течений, учитывают только

силу сопротивления давления.

Найдем уравнения, описывающие движение тела в вязкой среде, т.е. решим основную задачу динамики. Рассмотрим это решение на примере падения шарика в вязкой среде (см. рис.). Динамическое уравнение движения может быть записано в виде:

mg + F_с.т. + F_с.д. + F_арх. = ma (4)

В проекции на вертикальную ось Y это же уравнение записыва­ется так:

mg - F_с.т. - F_с.д. - F_арх. = ma (5)

Из трех сил лишь одна является переменной - это сила сопротивления, величина кото­рой быстро изменяется с увеличением скорости. Естественно, что с течением времени ускорение, с которым движется тело, будет уменьшаться, и наступит такой момент, когда оно станет равным нулю. Начиная с этого момента тело будет двигаться равно­мерно с постоян ной скоростью V_уст, величину которой можно найти из уравнения дви­жения при условии, что а=0.

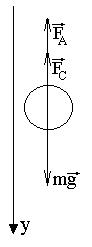Рис. 1

В зависимости от того, какая сила сопротивления преоб­ладает значение V_уст будет различным.

Законы движения, описывающие движение тела, можно найти, решая дифферен­циальное уравнение вида:

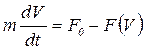(6)

где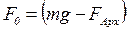

Список заданий

Задание 1: Экспериментально определить скорость установившегося движения шарика в глицерине и число Рейнольдса. Необходимые для расчета данные взять из справочной литературы или определить экспериментально.

Задание 2: Используя результаты работы записать зависимость V(t), Y(t), a(t).

Вопросы для зачета

1. Понятие пограничного слоя. Чем определяется толщина пограничного слоя?

2. Какое движение называют ламинарным, турбулентным?

3. Какие силы действуют на тело, движущееся в вязкой среде?

4. Каковы причины появления сил сопротивления давления и сопротивления трения?

5. Каков физический смысл и размерность коэффициента вязкости

6. Физический смысл числа Рейнольдса.

7. Напишите уравнение движения тела. Каков характер движения тела на отдельных участках?

8. Качественные графики зависимости скорости и ускорения тела, па­дающего в вязкой среде, от времени.

ЛАБОРАТОРНАЯ РАБОТА № 7