Выпуклость функции. Точки перегиба

Применение производной в исследовании функций.

Возрастание и убывание функций.

Теорема (критерий монотонности дифференцируемой функции).Пусть функция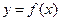непрерывна напромежутке 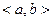и дифференцируема во всех его внутренних точках. Тогда:

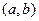
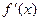
- для монотонного возрастания функции необходимо и достаточно, чтобы в 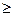0;

- для монотонного убывания функции необходимо и достаточно, чтобы в (а,в) 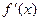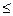0;

- для постоянности функции необходимо и достаточно, чтобы в (а,в) 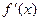=0.

Док-во. Докажем достаточность для возрастающей функции. Выберем произвольно точки 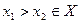. По теореме Лагранжа найдется точка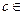 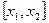, такая что 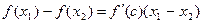. Т.к. оба множителя в правой части неотрицательны, то 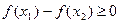, т.е. 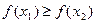. Следовательно, функция является монотонно возрастающей.

Докажем необходимость для возрастающей функции. Пусть f(x) – монотонно возрастает. Тогда 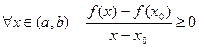, следовательно 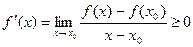в (а,в).

Для убывающей функции доказательства аналогичны.

Докажем необходимость для постоянной функции. Если f(x)=const в (а,в), то .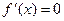

Докажем достаточность для постоянной функции. Пусть 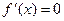в (a,b). Тогда тем более 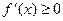в (a,b). Тогда по доказанному выше функция монотонно возрастает в (a,b), т.е. 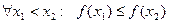. С другой стороны, если 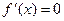в (a,b), то тем более 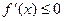в (a,b). Тогда по доказанному выше функция монотонно убывает в (a,b), т.е. 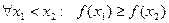. Одновременное выполнение этих условий возможно лишь при .▲

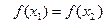Пример. Найти промежутки монотонности функции .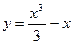

Найдем производную 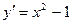. Очевидно, что при 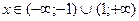производная 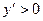, функция является возрастающей. При 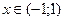производная 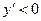, функция убывает.

Экстремумы функции.

Пусть функция 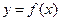задана на интервале .

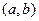Опр. Точка 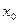называется точкой локального максимума функции f(x), если в некоторой ее окрестности выполняется условие: .

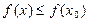Опр. Точка 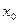называется точкой локального минимума функции f(x), если в некоторой ее окрестности выполняется условие: .

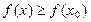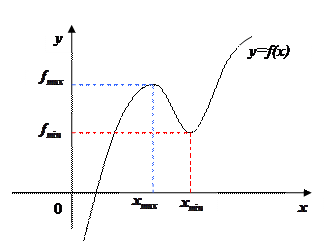
Значения функции в точках локального минимума и максимума называют минимумом и максимумом функции. Минимум и максимум функции объединяют в понятие «экстремум функции»

(extr f).

Отметить отличия локального и глобального экстремумов.

Теорема (необходимое условие локального экстремума).Еслидифференцируемаяфункция имеет экстремум в точке 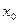, то ее производная в этой точке равна нулю: .

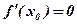Док-во. Если 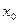- точка экстремума дифференцируемой функции, то существует некоторая окрестность этой точки, в которой выполнены условия теоремы Ферма. Тогда ее производная .

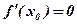Замечание. Функция может иметь экстремум и в точках, в которых она не дифференцируема (если эти точки входят в область определения). Например, функция 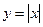имеет экстремум в точке х=0, но не дифференцируема в ней.

Точки, в которых производная равна нулю или не существует, называются стационарными или критическими точками. Из теоремы следует, что точки локального экстремума функции являются ее критическими точками. Обратное утверждение неверно. Например, функция 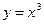имеет неотрицательную производную, т.е. возрастает на всей числовой оси, следовательно не имеет точек экстремума. В то же время, 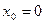является ее критической точкой.

Теорема (достаточное условие локального экстремума).Если при переходе через критическую точку 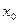производная дифференцируемой функции меняет знак с «+» на «-», то 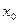- точка локального максимума, если с «-» на «+», то 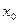- точка локального минимума.

Док-во. В соответствии с достаточным условием монотонности, функция возрастает слева от 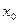и убывает справа, тогда в силу непрерывности функции, 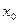является точкой максимума. Аналогичные рассуждения для минимума.

Замечание. Если при переходе через критическую точку производная не меняет знак, то в этой точке экстремума функции нет.

Теорема (2 достаточное условие локального экстремума). Для того, чтобы функция имела локальный максимум (минимум) в критической точке 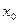, достаточно, чтобы в некоторой окрестности этой точки существовала непрерывная вторая производная и ( ).

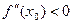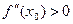(без док-ва).

Пример. Найти экстремумы функции ;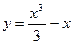

Ее производная: .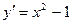

Определим критические точки: 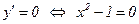, 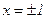- критические точки.

Определим знак производной в окрестностях критических точек.

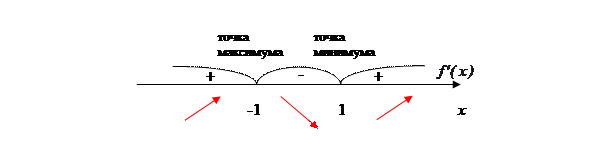
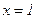- точка минимума, 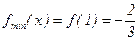- минимум функции;

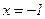- точка максимума, 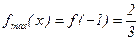- максимум функции.

§3. Наибольшее и наименьшее значения функции на отрезке.

При решении прикладных задач бывает нужно найти глобальные экстремумы функции на некотором промежутке. Если этот промежуток является отрезком, то экстремумы функция может достигать как в точках экстремума, так и на концах отрезка.

Пример. Найти наибольшее значение функции 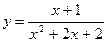на отрезке .

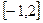Решение. Данная функция является непрерывной на данном отрезке (т.к. знаменатель не обращается в нуль), а следовательно, может принимать экстремальные значения либо в точках экстремума, либо на концах отрезка. Вычислим производную:

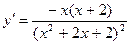. Тогда критическими точками являются точки х=0 и х=-2. Данному отрезку принадлежит только точка х=0. Вычислим значения функции в точке экстремума и на концах отрезка:

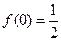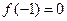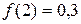, , . Сравнивая эти значения, заключаем, что наибольшее значение функции достигается в точке х=0.

Выпуклость функции. Точки перегиба.

Опр. Функция называется выпуклой вверх (выпуклой) на промежутке Х, если 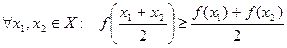. График выпуклой на промежутке Х функции расположен над любой ее секущей (и под любой ее касательной) на этом промежутке.

Аналогично вводится определение функции, выпуклой вниз (вогнутой).

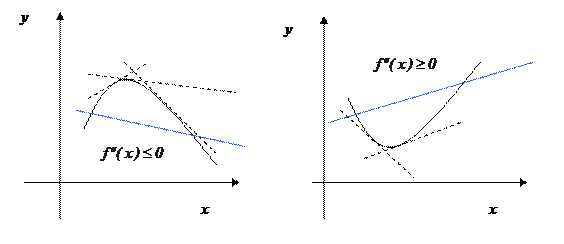
выпуклая (вверх) вогнутая (выпуклая вниз)

Теорема (критерий выпуклости функции). Пусть функция дифференцируема в интервале (а,в). Тогда для выпуклости функции вниз необходимо и достаточно, чтобы монотонно возрастала на этом интервале. Для выпуклости функции вверх необходимо и достаточно, чтобы монотонно убывала на этом интервале.

Следствие (достаточное условие выпуклости). Если вторая производная дважды дифференцируемой функции неотрицательна (неположительна) внутри некоторого промежутка, то функция выпукла вниз (вверх) на этом промежутке.

Опр. Точки, в которых график функции меняет направление выпуклости, называются точками перегиба графика функции.

Абсциссы точек перегиба являются точками экстремума первой производной.

Теорема (необходимое условие точки перегиба). Вторая производная дважды дифференцируемой функции в точке перегиба равна нулю: .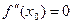

Абсциссы точек, в которых выполняется необходимое условие, называются критическими точками второго рода. Если перегиб графика есть, то только в таких точках.

Теорема (достаточное условие точки перегиба).Пусть 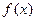- дважды дифференцируема в интервале (а,в). Тогда если вторая производная при переходе через критическую точку второго рода 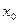меняет знак, то точка 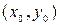является точкой перегиба графика функции.

Замечание. Если смены знака второй производной не происходит, то перегиба графика в точке нет.

Пример. 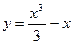, 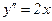; 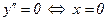- точка перегиба.

Итак, чтобы найти интервалы выпуклости функции, нужно:

1. Найти вторую производную функции.

2. Найти точки, в которых 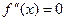или не существует.

3. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод о направлении выпуклости и точках перегиба на основании достаточных условий.