Основное уравнение динамики вращательного движения твердого тела с закрепленной осью вращения. момент импульса тела

Рассмотрим твердое тело, которое может вращаться вокруг неподвижной вертикальной оси (рис.5.3). Чтобы удержать ось от перемещений в пространстве, заключим ее в подшипники.

Абсолютно твердое тело – это система материальных точек с неизменным расстоянием между ними, и для всех его частиц (материальных точек) справедливо уравнение: 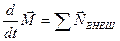. Это уравнение справедливо и для твердого тела. При этом под 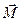следует понимать момент импульса тела, а 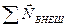есть сумма моментов всех внешних сил, .
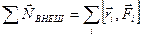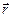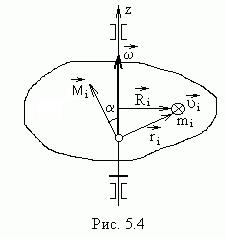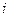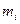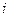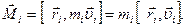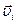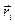Возьмем на оси вращения точку О и будем характеризовать положение образующих тело частиц радиус-векторами , проведенными из этой точки (на рис.5.3 показана -я частица с массой ). Момент импульса -той частицы относительно точки О равен Векторы и для всех частиц тела взаимно перпендикулярны, поэтому модуль вектора 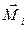равен

.

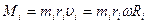Направление вектора 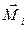показано на рис.5.4, его модуль пропорционален угловой скорости 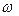. Направление 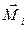не зависит от 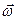, так как 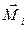лежит в плоскости, проходящей через ось вращения и частицу 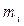, и перпендикулярен 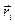. Проекция вектора 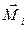на ось вращения 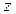, как следует из рис.5.4 , равна

.

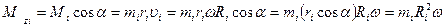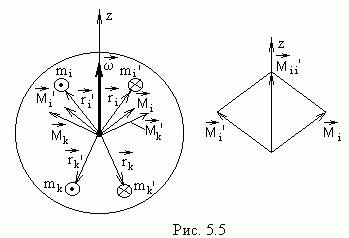
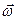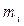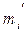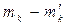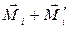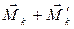Очевидно, для однородного тела вращения суммарный момент импульса направлен по оси вращения в ту же сторону, что и (рис.5.5). Действительно, разобьем тело на пары равных по массе и расположенных симметрично частиц (на рис. 5.5 показаны пары - и ). Сумма моментов каждой пары и направлена вдоль вектора 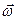, поэтому суммарный момент 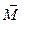также будет совпадать по направления с 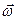, и модуль вектора 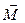равен его проекции на ось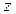

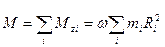. (5.1)

Величина 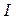, равная сумме произведений элементарных масс на квадраты их расстояний до некоторой оси, называется моментом инерции тела относительно этой оси:

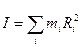. (5.2)

Тогда выражение (5.1) принимает вид:

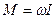. (5.3)

Так как векторы 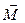и 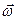имеют одинаковые направления, в векторной форме

получаем:

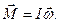(5.4)

Это выражение справедливо только для однородного тела, вращающегося вокруг оси симметрии. В общем случае оно не выполняется.

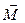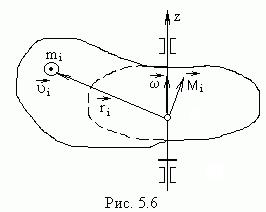
Для несимметричного или неоднородного тела момент импульса не совпадает по направлению с вектором 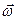. На рис.5.6 пунктиром выделена та часть несимметричного однородного тела, которая симметрична относительно оси вращения. Суммарный момент импульса этой части направлен вдоль 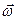. Момент 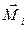каждой частицы, не входящей в симметричную часть, отклонен от оси вращения ( вправо для ситуации, представленной на рис.5.6). Полный момент импульса всего тела будет отклонен в ту же сторону (рис.5.7). При вращении тела вектор 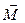поворачивается вместе с ним, описывая конус. За время 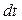вектор 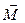получает приращение 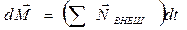. Если вектор 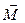не изменяется по величине, то вектор 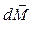направлен за чертеж на рис.5.7, так же направлен и вектор 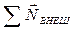. На этом рисунке момент внешних сил создается силами тяжести 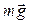(сила приложена в центре масс тела С), бокового давления подшипников на ось 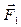и 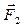, а также давления бортика подшипника на фланец 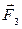. Силы трения отсутствуют.

Момент импульса относительно оси вращения для любого тела равен

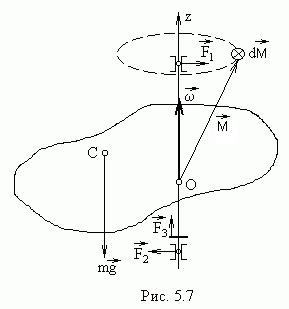
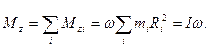(5.5)

В отличие от (5.4) эта формула выполняется для любого тела. Тогда

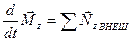. (5.6)

Подставив (5.5) в выражение (5.6), получаем

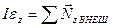, (5.7)

где 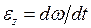- проекция углового ускорения на ось 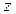. Уравнение (5.7) аналогично второму закону Ньютона 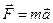. Роль массы играет момент инерции, роль линейного ускорения - угловое ускорение, роль суммарной силы - суммарный момент внешних сил. Поэтому (5.7) описывает динамику тела, вращающегося вокруг неподвижной оси, и называется основным уравнением динамики вращающегося тела.

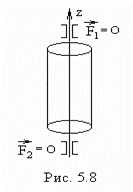
В случае вращения однородного симметричного тела силы бокового давления на подшипники не возникают (рис.5.8). В этом случае при отсутствии силы тяжести ось сохраняет свое положение в пространстве. Ось, положение которой в пространстве остается неизменным при вращении вокруг не тела в отсутствие внешних сил, называется свободной осью тела.

Для тела любой формы с произвольным распределением массы существуют три взаимно перпендикулярные, проходящие через центр масс тела оси, которые являются свободными осями. Они называются главными осями инерции тела.

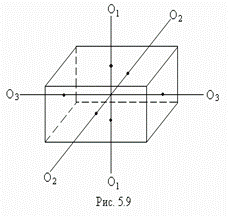
У однородного параллелепипеда (рис.5.9) главными осями инерции являются оси 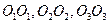, проходящие через центры противоположных граней.

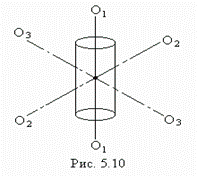У тела, обладающего осевой симметрией, например, у цилиндра (рис.5.10) одной из главных осей является ось симметрии, две другие – любые две взаимно перпендикулярные оси, лежащие в плоскости, перпендикулярной к оси симметрии и проходящие через центр масс тела. Таким образом, у тела с осевой симметрией фиксирована только одна из главных осей инерции.

У тела с центральной симметрией (шар) главными осями инерции являются любые три взаимно перпендикулярные оси, проходящие через центр масс, т.е. ни одна из главных осей не фиксирована.

Моменты инерции относительно главных осей называются главными моментами инерции тела. В общем случае эти моменты различны: 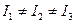. Для тела с осевой симметрией два главных момента одинаковы, а третий от них отличен, 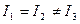. Такие тела называются симметричными волчками. У тел с центральной симметрией все три главных момента инерции одинаковы, эти тела называют шаровыми волчками.

Важной особенностью главных осей является то, что при вращении тела вокруг любой из них его момент импульса 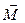совпадает по направлению с угловой скоростью 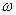и определяет­ся как 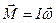, где 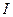- момент инерции тела относительно данной главной оси (Заметим, что последнее соотношение справедливо и относительно осей, параллель­ных главным осям тела и не проходящих через его центр масс). Причем 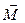не зависит от выбора точки, относительно кото­рой его определяют (здесь предполагается, что ось вращения неподвижна).

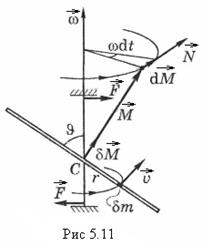
Если твердое тело привести во вращение и затем предоставить самому себе, то направление оси вращения в пространстве, вообще говоря, будет меняться. Для того чтобы произвольная ось вращения тела сохраняла свое направление неизменным, к ей необходимо приложить определенные силы. Рассмотрим этот вопрос более подробно на следующем примере. Пусть середина С однородного стержня жестко скреплена с осью вращения так, что угол между стержнем и осью равен 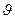(рис. 5. 11). Найдем момент 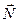внешних сил, которые необходимо приложить к оси вращения, чтобы при вращении стержня с угловой скоростью 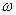ее направление не менялось. Согласно основному уравнению динамики вращательного движения, 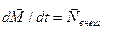. Таким образом, чтобы определить 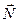, сначала надо найти момент импульса стержня 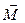, а затем его производную по времени. Момент импульса 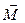проще всего определить относительно точки С. Мысленно выделим элемент стержня массы 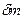, находящейся на расстоянии r от точки С. Его момент импульса относительно этой точки 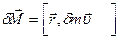,где 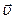- скорость элемента. Легко видеть, что вектор 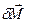направлен перпендикулярно стержню (рис. 5.11), причем его направление не зависит от выбора элемента 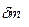. Поэтому суммарный момент импульса 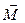стержня совпадает по направлению с вектором 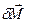. Заметим, что в данном случае вектор 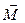не совпадает по направлению с вектором 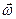! При вращении стержня вектор 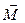будет также вращаться с угловой скоростью 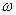. За промежуток времени 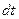вектор 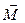получает приращение 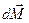, модуль которого, как видно из (рис. 5.11) равен 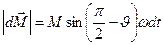, или в векторной форме .

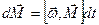Поделив обе части последне­го выражения на 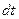, получим .

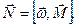Таким образом, действительно, для удержания оси враще­ния в неизменном направлении к ней необходимо в данном слу­чае приложить момент 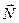некоторых внешних сил 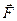(они пока­заны на рис. 5.11). Однако нетрудно видеть, что если 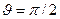, то вектор 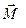совпадает по направлению с вектором 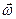, и в этом слу­чае , т. е. направление оси вращения будет оставаться не­изменным без внешнего воздействия.

Наиболее просто убедиться в справедливости 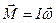можно для случая однородного тела с осевой симметрией. Действите­льно, момент импульса твердого тела относите­льно оси вращения 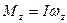( 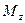- это проек­ция вектора 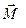, определенного относительно любой точки на этой оси). Но если тело симметрично относительно оси враще­ния, то из соображения симметрии сразу следует, что вектор 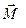совпадает по направлению с вектором 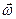и, значит, .

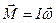В общем случае (ось вращения не сов­падает ни с одной из главных осей, хотя и проходит через центр масс тела) направление вектора 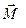не совпадает с векто­ром 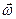, и связь между этими векторами носит сложный харак­тер. Это обстоятельство является причиной сложного поведе­ния вращающихся твердых тел.