Розв'яжіть завдання 2.1 — 2.4. Запишіть відповідь у бланк відповідей.
2.1. Знайдіть нулі функції у = х4 - 3х2 - 4.
2.2. Спростіть вираз 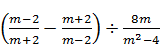
2.3. Кидають дві монети. Яка ймовірність того, що випаде один герб і одна цифра?
2.4. У трикутнику ABC відомо, що 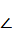 С = 90° , АС = 9 см, ВС = 12 см. На стороні АВ позначено точку D так, що AD = 5 см. Знайдіть відрізок CD.
С = 90° , АС = 9 см, ВС = 12 см. На стороні АВ позначено точку D так, що AD = 5 см. Знайдіть відрізок CD.
Частина третя
Розв'язання задач 3.1 - 3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1. При будь-якому n суму n перших членів деякої арифметичної прогресії
можна обчислити за формулою Sn=n2 + 3п . Знайдіть різницю цієї прогресії.
3.2. Першому робітнику для виконання завдання потрібно на 4 год більше, ніж другому. Якщо перший робітник буде працювати 3 год, а потім його змінить другий, то останньому потрібно буде працювати 6 год, щоб закінчити завдання. За скільки годин може виконати все завдання другий робітник?
3.3. Центр кола, описаного навколо трапеції, належить більшій основі, а бічна сторона дорівнює меншій основі. Знайдіть кути трапеції.
Варіант 30
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь та позначте її у бланку відповідей.
1.1. Яке з даних чисел можна записати у вигляді скінченного десяткового дробу?
А)  ; Б)
; Б)  ; В)
; В)  ; Г)
; Г)  .
.
1.2. Скоротіть дріб 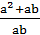
А) 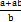 ; Б)
; Б) 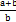 ; В)
; В) 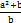 ; Г)
; Г) 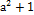 .
.
1.3. Обчисліть значення виразу 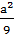 при а =
при а = 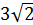
А)2; Б) 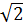 ; В)
; В) 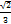 ; Г)
; Г)  .
.
1.4. Які координати точки перетину графіка рівняння 4х +7у = 28 з віссю ординат?
А) (7; 0); Б) (0; 7); В) (4; 0); Г) (0; 4).
1.5. Яка з послідовностей є арифметичною прогресією?
А) 2; 6; 10; 15; Б) 14; 17; 20; 23; В)-7;5;-3;1; Г) 12; 9; 6; 4.
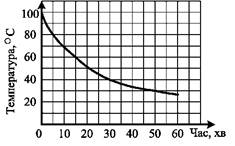 1.6. Після того як вода в чайнику закипіла, його вимкнули. На рисунку зображено графік зміни
1.6. Після того як вода в чайнику закипіла, його вимкнули. На рисунку зображено графік зміни
температури води в чайнику. За який час температура води знизилася з 60° до 40°?
A) 30 хв; Б) 25 хв; B) 20 хв; Г) 15 хв.
1.7. Областю значень якої з функцій є проміжок
[-2; + 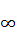 ) ?
) ?
А)у = х-2; Б)у = х2-2; В)у = -2х; Г)у =- 
1.8. Кирило купив 5 зошитів, після чого у нього залишилося 2,6 грн. Для покупки 8 зошитів йому не вистачило 1,6 грн. Скільки коштує один зошит?
А) 1 грн 20 коп.; Б) 1 грн 40 коп.; В) 1 грн 50 коп.; Г) 1 грн 60 коп.
1.9. Яка фігура є геометричним місцем точок площини, рівновіддалених від даної точки?
 А) промінь; Б) пряма; В) коло; Г) відрізок
А) промінь; Б) пряма; В) коло; Г) відрізок
1.10. На рисунку зображено прямокутник ABCD, 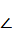 ACD = 43°. Яка величина кута AOD?
ACD = 43°. Яка величина кута AOD?
А) 86°; Б) 43°; В) 94°; Г) 137°.
1.11. На сторонах АВ і АС трикутника АВС, зображеного на рисунку, позначили точки М і К так , що АМ= 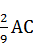 , АК=
, АК= 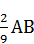 . Знайдіть сторону ВС, якщо МК=18 см
. Знайдіть сторону ВС, якщо МК=18 см
А) 4 см; Б) 36 см; В) 72 см; Г) 81 см.
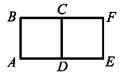 1.12. Квадрат CDEF, зображений на рисунку, є образом квадрата ABCD при повороті за годинниковою стрілкою на кут 90°. Яка точка є центром повороту?
1.12. Квадрат CDEF, зображений на рисунку, є образом квадрата ABCD при повороті за годинниковою стрілкою на кут 90°. Яка точка є центром повороту?
А) точка А; Б) точка С; В) точка D; Г) точка В
Частина друга
Розв'яжіть завдання 2.1 - 2.4. Запишіть відповідь у бланк відповідей.
2.1. Яку суму грошей треба покласти в банк під 10% річних, щоб через 2 роки на рахунку стало 6050 грн?
2.2. Розв яжіть систему нерівностей 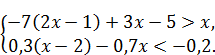
2.3. Спростіть вираз: 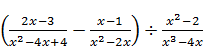
2.4. Перпендикуляр, опущений з точки перетину діагоналей ромба на його сторону, ділить її на відрізки 3 см і 12 см. Знайдіть площу ромба.
Частина третя
Розв'язання задач 3.1 — 3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1. Знайдіть область визначення функції у = 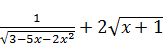
3.2. Першій бригаді для підготовки газону футбольного поля потрібно на 10 год більше, ніж другій. Коли перша бригада пропрацювала 12 год, а потім її замінила друга, яка пропрацювала 9 год, то було підготовлено 60 % газону. За скільки годин може підготувати газон кожна бригада, працюючи самостійно?
3.3. Центр кола, вписаного у рівнобедрений трикутник, ділить його висоту, проведену до основи, на відрізки, довжини яких дорівнюють 34 см і 16 см. Знайдіть площу даного трикутника.
Варіант 31
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь та позначте її у бланку відповідей.
1.1. Визначте пару взаємно простих чисел.
А) 7 і 14; Б) 14 і 16; В) 14 і 35; Г) 14 і 27.
1.2. Яка з нерівностей є правильною?
A) 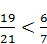 ; Б)
; Б) 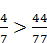 ; В)
; В) 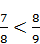 ; Г)0,(3)<
; Г)0,(3)< 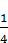 .
.
1.3. Спростіть вираз 45а4b5 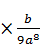 .
.
а) 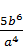 ; б)
; б) 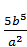 ;В)
;В) 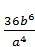 ; Г)
; Г) 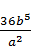 .
.
1.4. Укажіть вираз, який набуває тільки від'ємних значень.
А) х4-6 ; Б) -х4 -6; В)-х4+6; Г) -(х + 6)4.
1.5. Розв'яжіть систему нерівностей 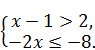
А)(3;+ 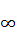 ); Б) [4; +
); Б) [4; + 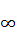 ); В) (-
); В) (- 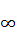 ; 3); Г) (-
; 3); Г) (- 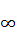 ; 4].
; 4].
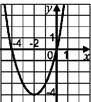 1.6. На рисунку зображено графік функції у = х2 + 4х. Користуючись рисунком, укажіть проміжок зростання функції.
1.6. На рисунку зображено графік функції у = х2 + 4х. Користуючись рисунком, укажіть проміжок зростання функції.
А) [-4; + 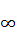 ); Б) [-3; +
); Б) [-3; + 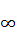 ); В)[-2;+
); В)[-2;+ 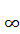 ); Г)(-
); Г)(- 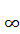 ;-4].
;-4].
1.7. У скільки разів хвилинна стрілка годинника рухається швидше, ніж годинна?
А) у 4 рази; Б) у 6 разів; В) у 9 разів; Г) у 12 разів.
1.8. Чому дорівнюють 20 % від числа 55 ?
А) 54 ; Б) 45 ; В) 5; Г) 1000.
1.9. Укажіть правильне твердження.
A) будь-який правильний многокутник має центр симетрії;
Б) якщо сторони опуклого многокутника рівні, то він є правильним;
B) будь-який правильний многокутник має осі симетрії;
Г) якщо суми протилежних сторін опуклого чотирикутника рівні, то навколо нього можна описати коло
1.10. Сторони трикутника відносяться як 7:6:4. Знайдіть більшу сторону подібного йому трикутника, менша сторона якого дорівнює 12 см.
 А) 84 см; Б) 56 см; В) 14 см; Г) 21 см
А) 84 см; Б) 56 см; В) 14 см; Г) 21 см
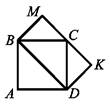
1.11. Площа квадрата ABCD, зображеного на рисунку, дорівнює 12 см2. Чому дорівнює площа прямокутника BMKD?
А) 16 см2; Б) 12 см2; В) 18 см2; Г) 24 см2.
1.12. 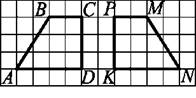 Укажіть рух, при якому образом чотирикутника ABCD, зображеного на рисунку, є чотирикутник MNKP.
Укажіть рух, при якому образом чотирикутника ABCD, зображеного на рисунку, є чотирикутник MNKP.
А) осьова симетрія;
Б) центральна симетрія;
В) паралельне перенесення;
Г) поворот
Частина друга
