Какая из формул является средней арифметической взвешенной?
1) 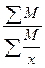 ; ; | 2) 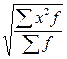 ; ; | 3) 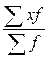 ; ; | 4) 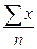 . . |
Какую среднюю можно определить по формуле: ?
1) среднюю гармоническую простую; 2) среднюю гармоническую взвешенную; 3) среднюю арифметическую простую; 4) среднюю квадратическую простую.
16. Какая из формул является средней гармонической взвешенной:
1) 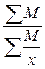 ; 2)
; 2) 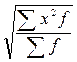 ; 3)
; 3) 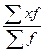 ; 4)
; 4) 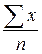 .
.
Какую среднюю можно определить по формуле ?
1) среднюю квадратическую простую; 2) среднюю хронологическую; 3) среднюю арифметическую простую; 4) среднюю гармоническую простую.
18. Какая из формул является средней гармонической простой:
1) 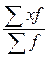 ; ; | 2) 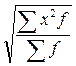 ; ; | 3) 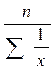 ; ; | 4) 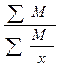 |
19. Какая из формул является средней квадратической взвешенной:
1) 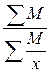 ; 2)
; 2) 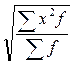 ; 3)
; 3) 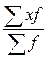 ; 4)
; 4) 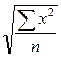
20. Какую среднюю следует применять, если отдельные значения признака в совокупности встречаются несколько раз:
1) среднюю гармоническую простую; 2) среднюю арифметическую простую; 3) среднюю гармоническую взвешенную; 4) среднюю арифметическую взвешенную.
Решение типовых задач
Пример 1. Валовой выпуск продукции отрасли составил в ба-зисном периоде 3500 тыс.грн. Планом на текущий период предус-мотрен выпуск на сумму 3800 тыс.грн., а фактическая его величина составила 3760 тыс.грн. Определите относительные величины плано-вого задания, выполнения плана и динамики.
Решение
1. Относительная величина планового задания:
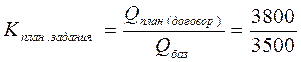 = 1,086 или 108,6%.
= 1,086 или 108,6%.
Таким образом, планировалось увеличить в отчетном периоде по сравнению с базисным валовой выпуск продукции в 1,086 раза или на 8,6% (108,6% - 100%).
2. Относительная величина выполнения плана: 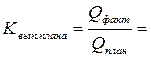 =
= 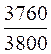 = 0,989 или 98,9%, т.е. план валового выпуска продукции вы-полнен на 98,9% или недовыполнен на 1,1% (98,9% -100%).
= 0,989 или 98,9%, т.е. план валового выпуска продукции вы-полнен на 98,9% или недовыполнен на 1,1% (98,9% -100%).
3. Относительная величина динамики: 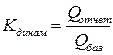
| |
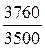 = 1,074 или 107,4%. В отчетном периоде по сравнению с базисным валовой выпуск продукции увеличился в 1,074 раза или на 7,4% (107,4% -100%). Взаимосвязь вычисленных показателей:
= 1,074 или 107,4%. В отчетном периоде по сравнению с базисным валовой выпуск продукции увеличился в 1,074 раза или на 7,4% (107,4% -100%). Взаимосвязь вычисленных показателей: 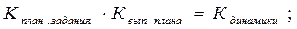 1,086 · 0,989 = 1,074.
1,086 · 0,989 = 1,074.
Пример 2.Планом производства на текущий год по сравнению с базисным было предусмотрено снижение себестоимости продукции на 3%, а фактически она была снижена на 2,5%. Определите относительную величину выполнения плана по снижению себестоимости продукции в текущем году.
Решение
Показатели заданы в процентах. По их содержанию определяем значения относительных величин: относительная величина планового задания по снижению себестоимости составляет 97% или Кплан.задания= = 0,97, а относительная величина динамики – 97,5% или Кдинамики = 0,975. Тогда относительная величина выполнения плана через взаимосвязь показателей будет равна: 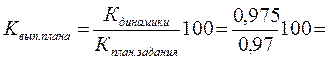
| |
Пример 3.За отчетный год в стране было зарегистрировано 9710 промышленных предприятий (без малых предприятий и кооперативов), в том числе по формам собственности: частная – 37; коллективная – 7141; государственная – 2516; собственность международных организаций и юридических лиц других государств – 16.
Определите все возможные относительные величины.
Решение
1.Относительная величина структуры:
d = 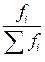 ; dчаст =
; dчаст = 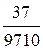 100 = 0,4%; dгосуд. =
100 = 0,4%; dгосуд. = 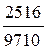 100 = 25,9%;
100 = 25,9%;
dкол. = 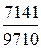 100 = 73,5%; dмеждунар.=
100 = 73,5%; dмеждунар.= 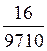 100 = 0,2%.
100 = 0,2%.
Наибольший удельный вес составляют предприятия коллективной формы собственности (73,5 %), на долю государственных предприятий приходится (25,9 %), малую долю составляют предприятия частные (0,4 %) и международные (0,2 %).
2. Относительная величина координации: примем за базу сравнения предприятия частной формы собственности: 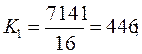
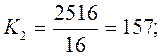
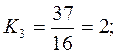 Ккоордин.= 446 : 157 : 2 : 1.
Ккоордин.= 446 : 157 : 2 : 1.
Это означает, что на одно предприятие частной формы собственности приходится 446 предприятий коллективной формы собственности, 157 государственной и 2 предприятия частных.
Пример 4. По городу имеются данные за год, тыс.чел.: число родившихся - 24,92; среднегодовая численность населения – 2800. Определить относительную величину интенсивности, характеризую-щую рождаемость.
Решение
Определим коэффициент рождаемости:
Крожд. = 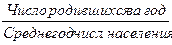 1000 =
1000 = 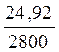 1000= 90/00. Это означает, что в расчете на каждую тысячу человек населения за год рождается 9 детей.
1000= 90/00. Это означает, что в расчете на каждую тысячу человек населения за год рождается 9 детей.
Пример 5.Заработная плата бригады строителей по отдельным профессиям за месяц характеризуется следующими данными:
| Маляры | Штукатуры | Кровельщики | |||
| Заработная плата, грн | Число ра-бочих, чел | Заработная плата, грн | Число ра-бочих, чел | Заработная плата, грн | Число рабочих, чел |
Определить среднюю заработную плату рабочих: а) по каждой профессии; б) в целом по бригаде.
Решение
1. Среднюю зарплату маляров определим по средней арифметической простой, так как каждый признак встречается в совокупности один раз: 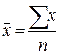 ;
; 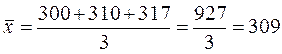 грн.
грн.
2.Среднюю зарплату штукатуров определим также по формуле средней арифметической простой, так как частоты равны между собой: 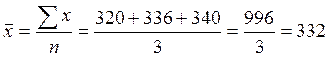 грн.
грн.
3. Среднюю зарплату кровельщиков определим по формуле средней арифметической взвешенной, так как каждый признак встречается неодинаковое число раз:
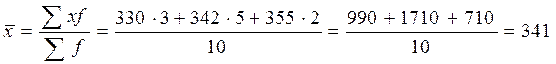 грн.
грн.
4.Средняя зарплата всех рабочих бригады строителей может быть определена как средняя арифметическая взвешенная из групповых средних: 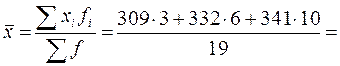 333,1 грн.
333,1 грн.
Пример 6. Средняя выработка продукции на одного рабочего за смену в двух цехах завода, вырабатывающих однородную продукцию, характеризуется следующими данными:
| Бригада № | Цех № 1 | Бригада № | Цех № 2 | ||
| дневная выработ- ка продукции,шт | число ра-бочих,чел | дневная выработ- ка продукции,шт | объем произведен-ной продукции,шт. | ||
| I | IV | ||||
| II | V | ||||
| III | VI |
Определить среднюю дневную выработку продукции рабочих по каждому цеху.
Решение
Логическая схема расчета:
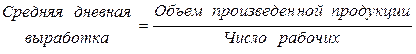
По первому цеху расчет произведем по средней арифметической взвешенной, поскольку по условию задачи известен знаменатель логической схемы расчета, т. е. число рабочих или частота появления признака: 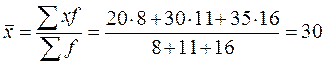 шт. По второму цеху – по средней гармонической взвешенной, т.к. известен числитель логической схемы расчета, т.е объем произведенной продукции:
шт. По второму цеху – по средней гармонической взвешенной, т.к. известен числитель логической схемы расчета, т.е объем произведенной продукции:
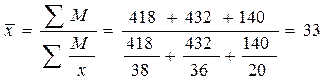 шт.
шт.
Пример 7.Три предприятия производят электромиксеры. Себестоимость одного миксера составляет: на 1-ом предприятии 50 грн, на 2-ом 60 грн, на 3-ем 80 грн. Определить среднюю себестоимость миксера при условии, что общие затраты на производство миксера на всех предприятиях одинаковы.
Решение
Составим исходную схему расчета:
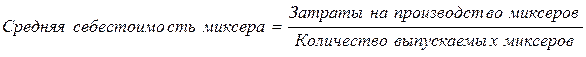 .
.
Так как общие затраты на всех предприятиях одинаковы, а значения признака (себестоимости) известны (x), расчет выполняем по средней гармонической простой:
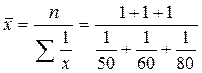 = 60,6 (грн).
= 60,6 (грн).
Пример 8. По данным о месячной зарплате 50-ти рабочих цеха определим среднюю зарплату:
| Группы рабочих по месячной зарплате, грн | Число ра-бочих, чел, f | Дискретный ряд, x | xf | Доля рабочих в коэф-тах, df | x df |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 400 - 420 | 0,04 | 16,4 | |||
| 420 - 440 | 0,08 | 34,4 | |||
| 440 - 460 | 0,16 | 72,0 | |||
| 460 - 480 | 0,4 | 188,0 | |||
| 480 - 500 | 0,32 | 156,8 | |||
| Итого: | - | 1,0 | 467,6 |
Решение
Данные о месячной зарплате рабочих цеха представлены в виде интервального ряда распределения (гр.1, 2). Для расчета средней месячной зарплаты необходимо перейти к дискретному ряду распределения. Определим середину каждого интервала (x) и запишем результаты в гр.3. Затем выполним расчет в 2-х вариантах:
1. Используя в качестве весов численность рабочих (f) (гр.4):
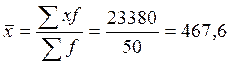 грн.
грн.
2. Используя в качестве весов долю рабочих в коэффициентах (df) (гр.5, 6): 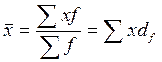 ;
; 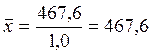 грн.
грн.
Пример 9.Члены садового товарищества постановили, что допустимый размер отклонения площади земельных участков от установленной нормы должен составлять 0,02 га. По следующим данным определите средний размер отклонения площади земельных участков от нормы:
| Отклонение, га | -0,03 | -0,02 | -0,01 | 0,03 | 0,04 | 0,05 | 0,06 | Итого | |
| Число участков |
Решение
Для ответа на вопрос задачи вычислим среднюю квадратическую взвешенную, т.к. значения признака представлены в виде отклонений и предварительно сгруппированы: 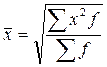 . Промежуточные вычисления выполним в таблице 4.1.
. Промежуточные вычисления выполним в таблице 4.1.
Таблица 4.1
Промежуточные расчеты для определения среднего размера
отклонения величины земельных участков от нормы
| Отклонения, га, x | Количество участков, f | x2 | x2f |
| 1 | 2 | 3 | 4 |
| - 0,03 | 0,0009 | 0,0108 | |
| - 0,02 | 0,0004 | 0,0072 | |
| - 0,01 | 0,0001 | 0,001 | |
| 0,03 | 0,0009 | 0,0225 | |
| 0,04 | 0,0016 | 0,0128 | |
| 0,05 | 0,0025 | 0,0175 | |
| 0,06 | 0,0036 | 0,018 | |
| Итого | - | 0,0898 |
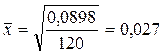 га. Средний размер отклонения величины земельных участков от нормы в ту и другую сторону составляет 0,027 га.
га. Средний размер отклонения величины земельных участков от нормы в ту и другую сторону составляет 0,027 га.
