Кинетическая энергия в обобщенных координатах

Для нестационарных связей радиус – вектор 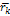зависит от всех обобщенных координат и времени t.

; ;

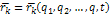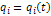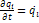
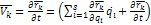(1)

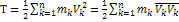i=1,2,…,s

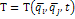
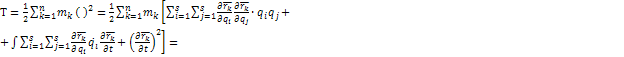
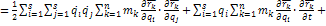
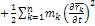В пустых скобках выражение (1)

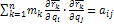
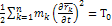
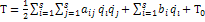
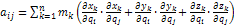
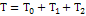
В общем случае кинетическую энергию материальной системы можно представить суммой квадратичной 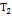, линейной 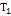и нулевой 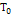форм относительно обобщенных скоростей.

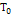- нулевая ступень обобщенных скоростей

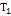- линейная функция обобщенных скоростей

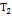- квадратичная степень обобщенных скоростей

Для стационарных связей: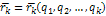

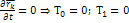
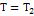
Одна степень свободы:

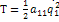
Две степени свободы:

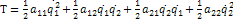
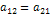
Уравнение Лагранжа II рода

Из формулы :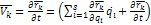

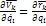
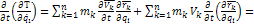
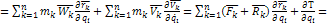
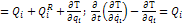
Связи идеальные:

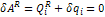
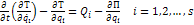
Силы только потенциальны:

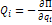
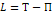(кинетический потенциал, функция Лагранжа)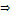

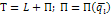
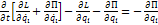
Обыкновенное однородное ДУ 2-го порядка (с нулевой правой частью):

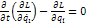“2S”

Число уравнения равно числу степеней свободы.