Угол между векторами и расстояние между точками. Доказать свойства расстояния

Косинус угла между векторами равен скалярному произведению, деленному на произведение моделей векторов.

Расстоянием называется величина вектора, соединяющего эти точки.

Свойства расстояния: 1) оно не отрицательно;

2) расстояние от А до В равно расстоянию В до А;

3) неравенство треугольника;

137) Ортогональность системы векторов. Доказать существование двух (трёх) ненулевых ортогональных векторов.

Ортогональные системы ненулевых векторов линейно независимы. (Доказывается записью 2-х скалярок, где один вектор представлен в виде линейной комбинации двух других.)

Существует 3 (2) ненулевых вектора.

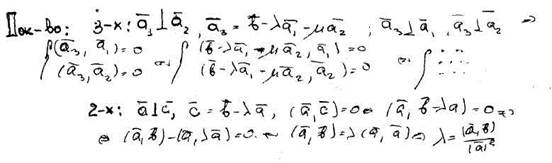
Доказать линейную независимость ортогональной системы векторов.

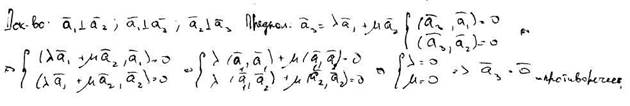
Проекция вектора на вектор.

Проекцией вектора а на вектор b называется скалярное произведение векторов а и b, деленное на модель вектора b.

Доказать теорему о проекции произведения вектора на число. Доказать теорему о проекции вектора на ось.

Т: Проекция произведения вектора на число равна произведению проекции этого вектора на число.(Выводится через определение)

Т: Проекция вектора на ось равна координатам вектора. (Выводится через определение)

Доказать, что в декартовой системе координаты вектора есть его проекции на оси координат.

Доказывается по определению.

Декартова система координат. Доказать теорему о скалярном произведении.

Декартовой системой координат называется аффинная система координат с ортонормированным базисом.

В декартовой системе координат скалярное произведение двух векторов равно сумме по парных произведений их координат.

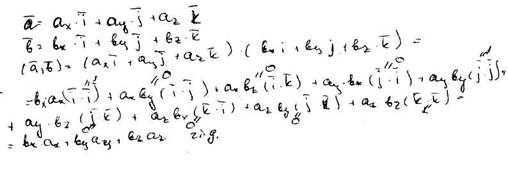
Доказать теоремы о длине вектора, расстоянии между точками и угле между векторами.

Т: В декартовой системе координат длина вектора равна квадратному корню из суммы квадратов координат.

Сл.: Расстояние между точками А и В равно квадратному корню из суммы квадратов разностей соответствующих координат (причём из координат 2-й точки вычитаются координаты 1-й).

Формула для вычисления косинуса угла та же.

Признак перпендикулярности прямой и плоскости.

О: Прямую, пересекающую плоскость, называют перпендикулярной этой плоскости, если она перпендикулярна ко всем прямым принадлежащим этой плоскости.

Т: Что бы прямая была перпендикулярна плоскости, необходимо и достаточно, что бы она была перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости.

Теорема о плоскости, проходящей через прямую перпендикулярную другой плоскости и обратная теорема.

Две плоскости, перпендикулярные одной и той же прямой, параллельны между собой.