Евклидово пространство, ортонормированные системы

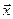Определение. Вещественное линейное пространство называется евклидовым пространством, если каждой паре поставлено в соответствие вещественное число, которое называется скалярным произведением векторов и 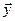, обозначается и для любых 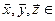, R удовлетворяет следующим требованиям:

1) ;

2) ;

3) , причем равенство возможно лишь в том случае, когда .

Утверждение. Арифметическое пространство Rⁿ, в котором скалярное произведение векторов задано равенством

,

является евклидовым пространством. Оно обозначается Eⁿ.

Определение. Векторы 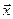и 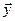называются ортогональными, если их скалярное произведение равно нулю.

Определение. Нормой (длиной) вектора называется число .

Определение. Углом между ненулевыми векторам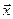и и 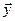назы­вается угол такой, что

.

Определение. Система ненулевых векторов 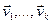называется ортого­нальной системой, если скалярное произведение любых двух различных векторов этой системы равно нулю.

Утверждение. Ортогональная система линейно независима.

Определение. Ортогональная система векторов 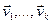называется ортонормированной системой, если норма любого вектора из этой системы равна единице.

Процесс ортогонализации базиса. Пусть даны линейно независимых векторов . Для построения по этим векторам попарно ортогональных векторов необходимо провести следующую процедуру ортогонализации. Положим вначале . Затем вектор будем искать в виде .

По условию ортогональности . Следовательно, откуда .

Предположим, что уже построено ортогональных векторов . Будем искать в виде

.

По условию вектор должен быть ортогонален , что даёт уравнений для определения неизвестных . Выпишем эти уравнения с учётом ортогональности векторов :

откуда получим

Примеры

1. В евклидовом пространстве построить ортонормированный базис по данному

Решение. Проведём вначале ортогонализацию, т.е. построим ортогональный базис . Проверим прежде всего, нет ли среди векторов ортогональных. Вычислим :

.

Откуда следует, что векторы и ортогональны. Они сразу входят в состав ортогонального базиса .

Далее определим , пользуясь процедурой ортогонализации. Ищем в виде .

Из условий ортогональности имеем

.

Таким образом

Теперь отнормируем базис , т.е. переведём его в ортонормированный базис , получим

2. Дополнить до ортогонального базиса пространства систему векторов

Решение. Вначале ортогонализируем . Положим . Исходя из условия .

Построим . Пусть . По условиям ортогональности , откуда имеем

.

Общее решение полученной системы есть

ФСР строится стандартным способом и состоит из двух линейно независимых решений:

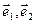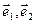Вектор ортогонален векторам и, следовательно, входит в ортогональный базис. Вектор также ортогонален , но не ортогонален . Действительно

.

Проверим теперь, является ли система векторов линейно независимой. Для установления факта зависимости (независимости) этих векторов вычислим а»):

Неравенство нулю этого определителя означает, что однородная система уравнений для коэффициентов линейной комбинации рассматриваемых векторов имеет лишь тривиальное решение. Следовательно, векторы линейно независимы и составляют базис в пространстве . Остаётся теперь ортогонализировать вектор . Следуя стандартной процедуре, ищем в виде

Таким образом окончательно в качестве ортогонального базиса в имеем .

Задачи

3.49. Найти нормы векторов 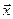и 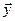, их скалярное произведение и косинус угла между ними, если

а) , ; б) , ;

в) , .

3.50. Найти длины сторон и внутренние углы треугольника , вершины которого заданы своими координатами: , , .

3.51 Установить, что данная система векторов является ортогональной, и получить из нее ортонормированную систему:

а) , ; б) , , ;

в) , , .

3.52. Ортогонализировать систему векторов:

а) , ; б) , , ;

в) , , .

3.53. Построить ортонормированный базис линейной оболочки векторов:

а) , ; б) , , ;

в) , , , .

3.54. Дополнить до ортогонального базиса пространства Еⁿсистему векторов:

а) ; б) , ; в) , , ; г) , .

3.55. Дополнить до ортонормированного базиса пространства Еⁿсистему векторов:

а) ; б) , ;

в) , .

3.56. Доказать, что линейное пространство непрерывных на отрезке функций является также евклидовым пространством, если в нем скалярное произведение двух произвольных функций и задано следующим образом:

.

Записать в этом пространстве неравенство треугольника и неравенство Коши-Буняковского.

3.57. Считая, что в евклидовом пространстве из предыдущей задачи , , найти

а) длину вектора ;

б) длину вектора ;

в) скалярное произведение векторов и ;

г) скалярное произведение векторов и ;

д) угол между векторами и ;

е) угол между векторами и .

3.58. Проверить, что в пространстве непрерывных на отрезке функций со скалярным произведением, заданным формулой

,

функции образуют ортогональную систему. Получить из нее ортонормированную систему.

Матрица Грама

Определение. Матрицей Грама для системы векторов 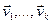называется симметричная матрица вида

,

где .

Утверждение. Скалярное произведение векторов и , заданных в базисе 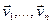, вычисляется по фор­муле

,

где - матрица Грама для системы векторов .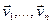

Определение. Подмножество евклидова пространства Еⁿ вида

,

где - линейно независимые векторы, называется k-мерным параллелепипедом, построенным на векторах .

Утверждение. Объем k-мерного параллелепипеда, построенного на векторах , равен квадратному корню из определителя матрицы Грама для системы векторов .

Задачи

3.59. Построить матрицу Грама для системы векторов:

а) , ;

б) , , ;

в) , .

3.60. Вычислить скалярное произведение векторов 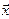и 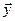, заданных своими координатами в базисе 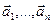, если

а) , , , ;

б) , , , , .

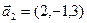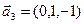3.61. Вычислить длины векторов 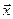, 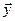и угол между ними, если даны следующие разложения по базису 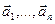и ортонормированному базису :

а) , , , ;

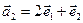б) , , , ;

в) , , , , .

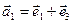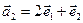3.62. Найти площадь параллелограмма, построенного на векторах:

а) , ; б) , ;

в) , .

3.63. Вершины треугольника заданы своими координатами: , , . Найти

а) длину медианы, проведенной из вершины ;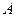

б) площадь треугольника ;

в) длину высоты, опущенной из вершины .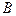

3.64. Найти объем параллелепипеда, построенного на векторах:

а) , , ;

б) , , .

3.65. Основание параллелепипеда, построенного на векторах , лежит в плоскости векторов . Найти высоту параллелепипеда, проведенную к основанию, если в ортонормированном базисе справедливо разложение , , .

3.66. Вершины пирамиды заданы своими координатами: , , , . Найти объем пирамиды, длину высоты, опущенной из вершины на основание , и угол наклона бокового ребра к плоскости основания.

3.67. В евклидовом пространстве Еⁿ под n-мерным единичным кубом понимается множество вида

,

где векторы 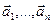образуют ортонормированную систему. Требуется

а) найти число диагоналей n-мерного куба;

б) найти число его диагоналей, ортогональных данной диагонали;

в) найти длину диагонали куба;

г) доказать, что любая диагональ куба образует равные углы со всеми его ребрами; найти этот угол и его предел при .

Унитарное пространство

Определение. Линейное пространство называется унитарным пространством, если каждой паре поставлено в соответствие комплексное число, которое называется скалярным произведением 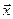на 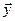, обозначается , и для любых и комплексных удовлетворяет следующим требованиям:

1) ;

2) ;

3) , причем равенство возможно лишь том случае, когда .

Утверждение. Комплексное линейное пространство

Uⁿ= ,

в котором скалярное произведение векторов задано равенством

,

является унитарным пространством.

Примеры

1. Векторы образуют ортонормированный базис в унитарном пространстве. Найти скалярное произведение , если

.

Решение. В рассматриваемом случае в соответствии со свойствами скалярного произведения в унитарном пространстве можно записать

2. В унитарном пространстве со скалярным произведением

вида построить ортонормированный базис по данному

.

Решение. Сначала проведём процедуру ортогонализации. В данном случае она аналогична описанной для евклидова пространства. Положим

.

Используя условия ортогональности, получим

.

Теперь отнормируем векторы :

Задачи

3.68. В унитарном пространстве Uⁿ вычислить скалярное произведение:

а) на ; б) на ;

в) на ; г) на .

3.69. Ортогональны ли векторы:

а) и ; б) и ;

в) и .

3.70. В унитарном пространстве Uⁿ вычислить норму вектора:

а) ; б) ; в) ; г) .

3.71. Построить матрицу Грама системы векторов:

а) , , ; б) , .

3.72. Векторы образуют ортонормированный базис пространства U². Найти скалярное произведение и , если

а) , ;

б) , .

3.73. Векторы 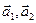образуют ортогональный базис пространства U². Найти и , если

а) , , , ;

б) , ,

, .

3.74. Ортонормировать систему векторов:

а) , ; б) , .

3.75. Показать, что линейное пространство

не будет являться унитарным, если в нем скалярное произведение на задать равенством .