Исследование операций и принятие решений
Любая целенаправленная деятельность сопровождается принятием решений.
Под термином «исследование операций» понимают применение математических, количественных методов для обоснования принимаемых решений во всех областях человеческой деятельности.
Операцией называют комплекс мероприятий направленных на достижение поставленной цели. Операция является управляемым мероприятием.
Прежде всего это относится к планированию сложных систем, которые возникают в экономике, экологии, социальной сфере. Хотя экономисты, управленцы, военные и т.д. принимают решения каждый в своей сфере деятельности, методы и критерии, которыми они руководствуются, по существу, одни и те же. Эти методы и составляют предмет теории принятия решений.
Процесс принятия решения можно условно разбить на части:
1. определение цели и критериев,
2. построение моделей,
3. разработка методов поиска оптимального решения,
4. экспертиза моделей,
5. выбор приемлемых альтернативных вариантов и их сравнение,
6. нахождение линии оптимального поведения в рамках выбранного варианта,
7. распределение интеллектуальных и материальных ресурсов и т.д.
При анализе той или другой ситуации выбирают соответствующий критерий оценки, который называют показателем эффективности или целевой функцией. Это может быть, например, средняя прибыль предприятия, количество сбитых самолетов и т.п., но также и вероятность получения заданной средней прибыли, вероятность обнаружения самолета и т.п.
Затем строится математическая модель рассматриваемой ситуации или рассматриваемого объекта и ищется max (или min) целевой функции при заданных ограничениях. Построение модели требует специальных знаний и хорошей математической подготовки. Методы математического программирования (планирования) предполагают компьютерную реализацию. Модель тестируется и корректируется до тех пор, пока не будет достигнуто соответствие между объектом и моделью. Полученное математическое решение облекается в содержательную форму и представляется в виде рекомендаций.
Окончательное решение остается за ответственным лицом, который должен наряду с рекомендациями математического расчета учесть и не вошедшие в расчет соображения.
Если известны все действующие в системе факторы, т.е. отсутствуют случайные воздействия, то это будет принятие решения в условиях определенности.
Если выбранное решение приводит с разной вероятностью к одному из возможных исходов, то принимающий решение рискует получить не тот результат, на который надеется. Этот случай называют принятием решений в условиях риска.
Если в момент принятия решения какие-либо факторы неизвестны, например погодные условия, действия противника и т.п., то такая задача называется принятием решений в условиях неопределенности. Природа неизвестных факторов различна. Если неизвестные факторы представляют собой случайные величины, для которых известны законы распределения вероятностей и другие статистические характеристики, то такие задачи исследования операций называются стохастическими.
В условиях неопределенности выбор варианта должен определяться двумя факторами:
- знанием вероятностей возможных исходов (последствий);
- знанием предпочтений, отдаваемых различным исходам.
В согласии с теорией принятия решений следует выделять следующие этапы:
1. определение альтернативных способов действия;
2. описание вероятностей возможных исходов;
3. ранжировка предпочтений возможных исходов через их полезность;
4. рациональный синтез информации, полученный на первых трех этапах.
Новые возможности ЭВМ позволили создать так называемые системы поддержки принятия решений. Эти системы содержат базы знаний об исследуемой области, набор ситуаций и рекомендуемых к ним вариантов решения, опыт других лиц, модели и правила.
Несмотря на объективность математических методов, полученное решение нельзя рассматривать как истину в последней инстанции, так как при отсутствии полной исходной информации математическая теория и научно обоснованные методы не дают точного решения. Можно сказать, что метод исследования операций – искусство давать плохие советы, когда другие методы дают еще худшие.
К тому же даже самый тщательный выбор решения не гарантирует успех навечно. Через определенный период времени каждое решение надо пересматривать. Научные методы лишь помогают принять решение. Никакая ЭВМ не сможет принять решение вместо человека и взять на себя ответственность за последствия этого решения.
Часто решения приходится принимать в конфликтных ситуациях, когда сталкиваются интересы и цели двух и более сторон. Математическая теория, анализирующая конфликтные ситуации, называется теорией игр.
ПРИЛОЖЕНИЕ
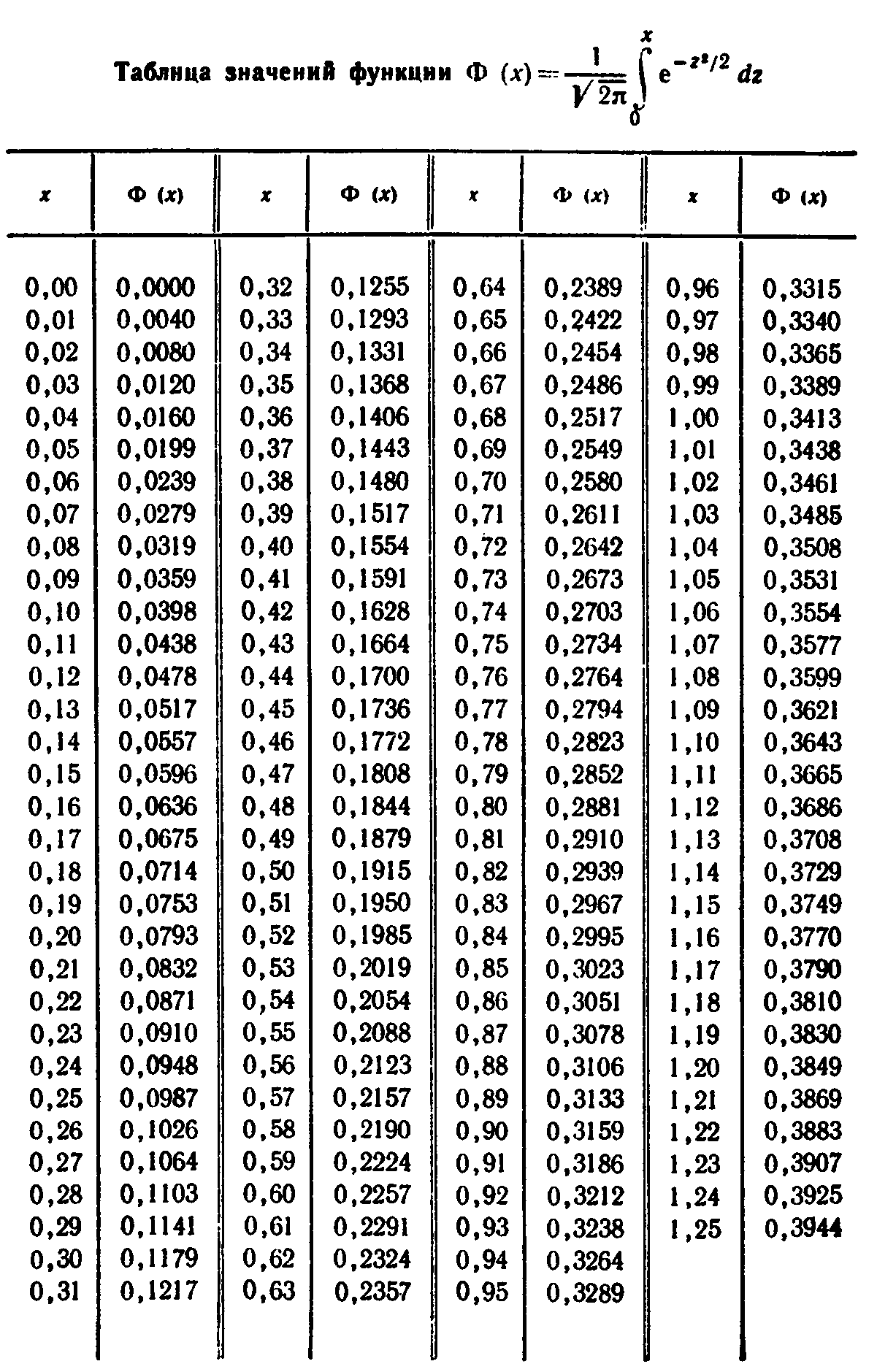
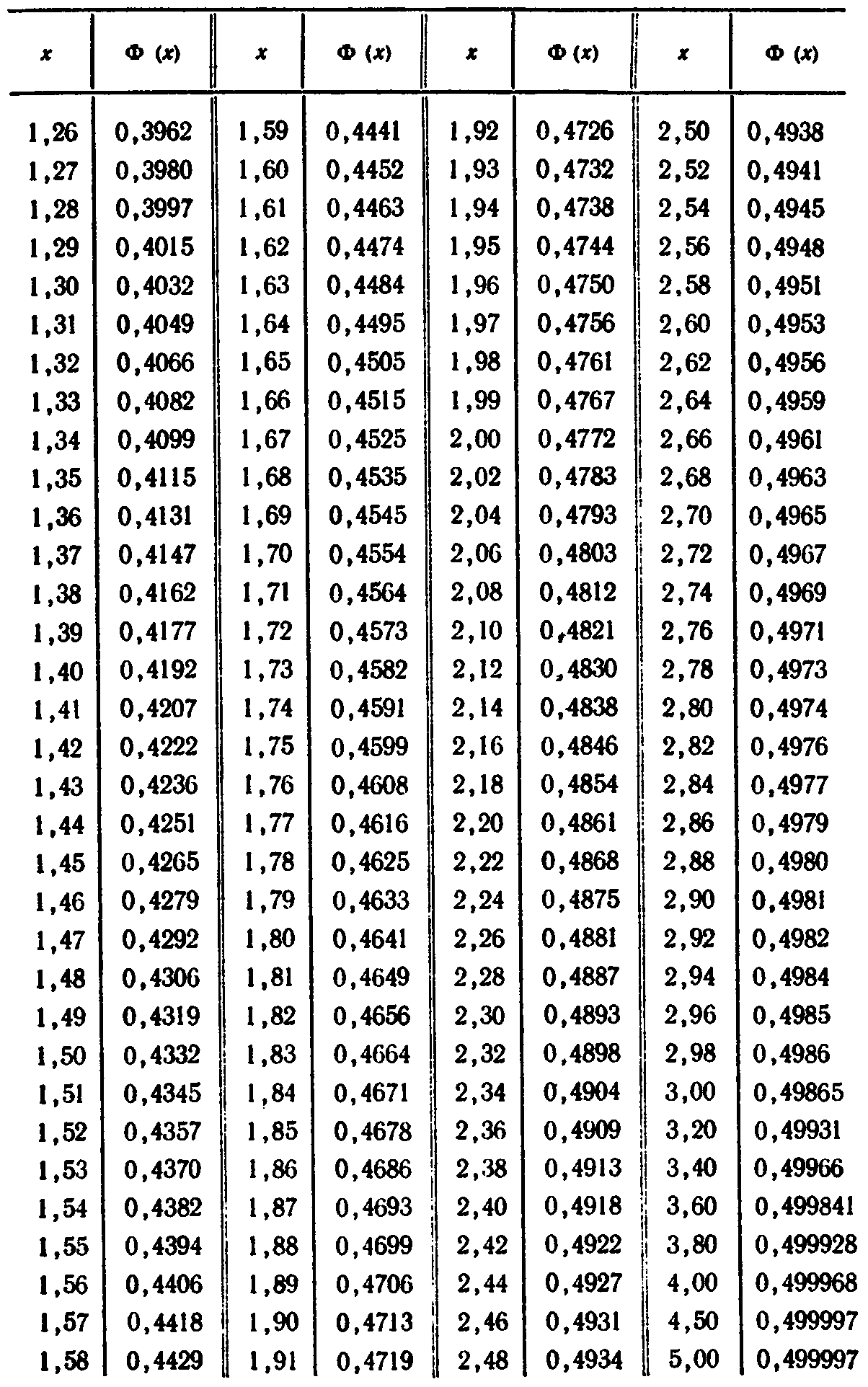
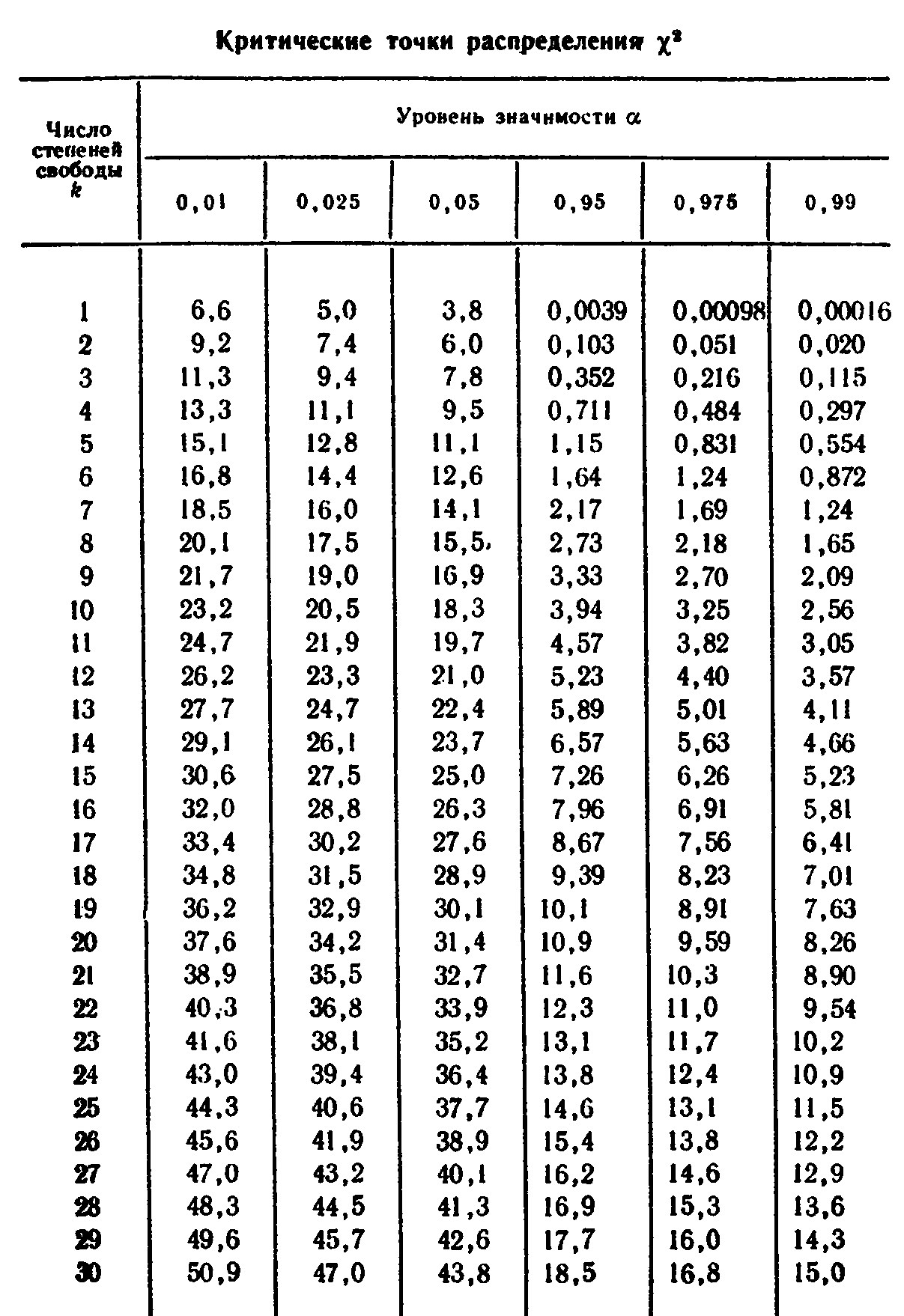

БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Турецкий В.Я. Математика и информатика: учеб, пособие для вузов / В.Я. Турецкий. – 3-е изд., перераб. и доп. – М.: ИНФРА, 2006. – 560 с.
2. Грес П.В. Математика для гуманитариев: учеб. пособие. для вузов / П.В. Грес. – М.: Логос, 2003 – 120 с.
3. Козлов В.Н. Математика и информатика: учеб. пособие для вузов / В.Н. Козлов. – СПб.: Изд-во СПбГТУ, 2001. – 266 с.
4. Елисеева И.И. Теория статистики с основами теории вероятностей: учеб. пособие для вузов / И.И. Елисеева, В.С. Князевский, Л.И. Новорожкина, З.А. Морозова; под ред. И.И. Елисеевой. – М.: ЮНИТА-ДАНА, 2001. – 446 с.
5. Вентцель Е.С. Теория вероятностей и ее инженерные приложения: учеб. пособие для втузов / Е.С. Вентцель, Л.А. Овчаров. – 2-е изд., стер. – М.: Высш. шк., 2000. – 480 с.
6. Виленкин Н.Я. Задачник-практикум по теории вероятностей с элементами комбинаторики и математической статистике: учеб. пособие для вузов / Н.Я. Виленкин, В.Г. Потапов. – М.: Просвещение, 1979. – 111 с.
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ 3
1 ОСНОВHЫE ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА 4
1.1 Математика как часть общечеловеческой культуры. Основные этапы становления современной математики. Аксиоматический подход 4
1.2 Множества и подмножества. Операции над множествами. Мощность множества 11
1.3 Множество действительных и комплексных чисел 17
1.4 Линейные пространства. Векторы и операции над ними. Координаты вектора в заданном базисе 21
1.5 Понятие матрицы. Квадратные матрицы и их определители. Формулы Крамера 24
1.6 Топологические понятия. Последовательности. Предел и непрерывность функции 29
1.7 Производная и дифференциал функции.Экстремум функции. Правила Лопиталя 36
1.8 Первообразная, неопределенный и определённый интегралы. Формула Ньютона–Лейбница 41
1.9 Понятие о дифференциальных уравнениях. Задача Коши 45
2 ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ВЕРОЯТНОСТИ 48
2.1 Предмет теории вероятности. Случайные события. Действия над случайными событиями 48
2.2 Классическое определения вероятности. Комбинаторика 53
2.3 Статистическое определения вероятности. Частота и вероятность 55
2.4 Геометрическое определения вероятности 57
2.5 Теоремы сложения и умножения вероятностей. Условная вероятность. Независимость событий 58
2.6 Формула полной вероятности 62
2.7 Формула Байеса 64
2.8 Схема испытаний Бернулли 65
2.9 Понятие случайной величины. Числовые характеристики дискретных случайных величин 66
2.10 Основные законы распределения дискретных случайных величин 72
2.11 Числовые характеристики непрерывных случайных величин 76
2.12 Основные законы распределения непрерывных случайных величин. Нормальное распределение 83
2.13 Зависимость двух случайных величин. Коэффициент корреляции 89
2.14 Предельные теоремы теории вероятностей 92
3 ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 98
3.1 Предмет математической статистики. Генеральная и выборочные совокупности 98
3.2 Эмпирическое распределение. Точечные оценки параметров распределения генеральной совокупности 102
3.3 Интервальные оценки. Доверительные интервалы для параметров нормального распределения 110
3.4 Проверка статистических гипотез. Проверка гипотез о законе распределения 117
4 ПРИНЦИПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ 122
5 ИССЛЕДОВАНИЕ ОПЕРАЦИЙ И ПРИНЯТИЕ РЕШЕНИЙ 125
ПРИЛОЖЕНИЕ 128
БИБЛИОГРАФИЧЕСКИЙ СПИСОК 132
Учебное издание
Шунина Валентина Алексеевна
Пешков Вадим Вячеславович
Кострюков Сергей Александрович
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА,
ТЕОРИИ ВЕРОЯТНОСТИ И СТАТИСТИКИ
В авторской редакции
Компьютерный набор В.В. Шуниной
Подписано к изданию 11.06.2014.
Объем данных 2,73 Мб.
ФГБОУ ВПО «Воронежский государственный технический университет»
394026 Воронеж, Московский просп., 14
