Явление переноса в газах. Уравнение переноса

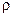Хаотичное движение газовых молекул ведет к непрерывному перемешиванию газа. С этим связано ряд важных явлений, происходящих в газах. Например, если в разных частях сосуда с газом плотность газа различная, то с течением времени она выравнивается. Точно также два различных газа, находящихся в соприкосновении перемешиваются между собой. Эти явление называются диффузией.

В объеме газа, части которого имели первоначально различные температуры, происходит постепенное выравнивание температуры, за счет переноса молекулами своей энергии 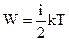и обмена энергиями с другими молекулами при перемешивании. Это явление называется теплопроводностью. Рассмотрим еще одно явление. Пусть газ течет вдоль горизонтальной поверхности АВ. Ближайший к поверхности слой имеет меньшую скорость благодаря трению о поверхность. Скорости разных слоев газа показаны на рисунке 6. Между слоями газа возникает сила трения, обусловленная переносом молекулами из слоя в слой количества движения 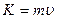. Это явление называется внутренним трением или вязкостью. Благодаря внутреннему трению газ движется вблизи поверхности параллельными слоями, скорости которых убывают в направлении перпендикулярном к поверхности АВ. Все перечисленные явления обусловлены одной причиной - переносом молекулами газа своих физических характеристик: массы (диффузия), энергии (теплопроводность), количество движения (явление внутреннего трения). Поэтому механизм всех этих явлений является одинаковым, и все они объединены под общим названием - явление переноса.

Исходя из молекулярно-кинетической теории, выведем общее для всех явлений переноса уравнение переноса. В пространство, где находится газ с концентрацией 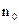, введем декартовую систему координат (рис.7).

Перпендикулярно оси Х поместим поверхность площадью 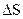. Определим количество молекул, проходящих через эту поверхность за время .

Рис.7

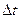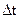За время через 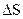пройдут 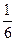часть всех молекул, находящихся внутри параллелепипеда с основанием 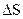и высотой 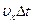. Число таких молекул будет равно

.

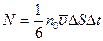Эти молекулы переносят через площадку 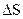значения своих характеристик 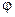(масса, энергия, количество движения). Тогда количество физических характеристик, перенесенных молекулами в одном направлении через 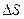за время 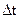определится выражением:

.

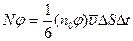Такое же количество физической характеристики будет перенесено и в обратном направлении, т.е. поток физической характеристики через 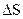будет равным нулю.

Предположим, что рассматриваемый газ неоднороден по своим свойствам, т.е. 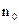различно в разных местах объема, а сами молекулы имеют неодинаковые значения 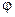. Тогда 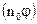будет также различным в разных местах объема газа. Пусть 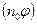убывает в положительном направлении оси Х.

Выберем две площади, находящиеся на одинаковых расстояниях от площади 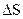, равных длине свободного пробега 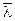(Рис.8). Тогда 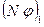будет связано переносом физической характеристики по направлению оси Х.

Такой же поток физической характеристики 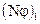в направлении оси Х будет и через площадь 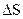, так как эти площади находятся на расстоянии длины свободного пробега, и в этом промежутке обмен значениями 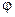и изменение 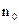не происходит, поскольку молекулы не испытывают столкновения. Также рассуждая, можно предположить, что через площадь 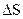в обратном направлении оси Х, будет поток физической характеристики 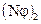, причем 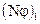> 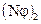. Тогда результирующий поток физической характеристики через 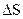будет равным:

.

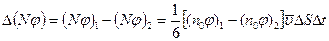Разделив и умножив правую часть полученного выражения на 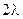, перепишем в виде:

.

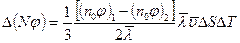Поскольку 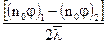представляет изменение 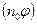на единицу длины, мы можем переписать выражение для 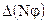в виде:

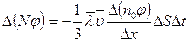. (4.3)

Полученное выражение представляет уравнение переноса. Знак (-) обусловлен тем, что перенос физической величины происходит в направлении противоположном 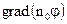, 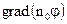определяет направление максимального роста .

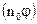Диффузия

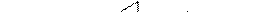Пусть в некотором объеме газа имеет место неоднородность в отношении плотности 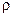, причем плотность 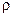убывает в направлении оси Х. Предположим,

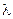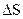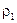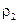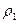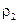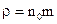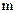что плотности на расстоянии влево и вправо от площади , равны соответственно и (Рис.9). Тогда > . Поскольку , где - масса молекулы, одинаковое для всех молекул газа, 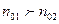. Переносимой величиной в случае диффузии является масса, т.е. 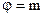. Тогда в выражении (4.3)

, .

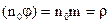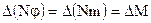Окончательно имеем:

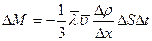. (4.4)

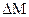- масса газа, переносимая благодаря диффузии через площадь 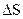, перпендикулярной направлению оси Х, за время 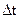. В термодинамике необратимых процессов уравнение диффузии определяется эмпирическим законом Фика:

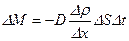, (4.5)

где D- коэффициент диффузии. Из уравнений (4.4) и (4.5) следует, что коэффициент диффузии определяется следующим выражением:

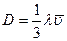. (4.6)

Единица измерения коэффициента диффузии в системе СИ .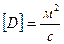

Рассмотрим, как зависит коэффициент диффузии от термодинамических параметров. Из формулы (4.6) следует, что 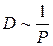, поскольку 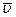не зависит от давления, а 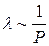. Таким образом, с ростом давления Р коэффициент диффузии уменьшается. Определим зависимость коэффициента диффузии от температуры. Так как длина свободного пробега практически не зависит от температуры, а 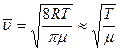, имеем 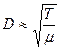. Кроме того, D зависит от сорта газа, эта зависимость определяется тем, что в выражении для коэффициента диффузии входит молярная масса газа .

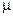Нестационарная диффузия

Рассматриваемый выше процесс диффузии называется стационарным. При стационарной диффузии градиент концентрации остается постоянным, соответственно, остается постоянным и диффузионный поток. Если градиент концентрации изменяется со временем, то диффузия называется не стационарной.

Рассмотрим процесс нестационарной диффузии, когда происходит выравнивание концентрации в следующем простейшем случае.

Пусть два сосуда с объемам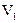и и 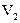соединены между собой трубкой длиной l с площадью сечения 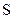и наполнены смесью газов разного состава при одинаковых давлениях и температурах (рис.10). Пусть концентрации интересующей нас компоненты в обоих сосудах равны 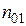и 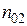. Вследствие диффузии концентрации в обоих сосудах будут выравниваться, т.е. будет убывать со временем разность концентраций

.

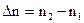Определим, по какому закону происходит это убывание. Из закона Фика, записанного для переносимого числа частиц, имеем:

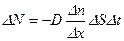. (4.7)

Предположим, что концентрация рассматриваемой компоненты мала, так что можно положить:

.

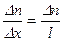В процесс диффузии молекулы интересуемой компоненты будут переходить из сосуда I в сосуд II. За бесконечно малый промежуток времени 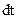число молекул, продиффундировавших в сосуд II равно:

.

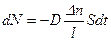Из-за такого перехода молекул их плотность в сосуде I уменьшается на некоторую величину 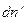, а в сосуде II увеличивается на величину 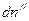, причем

.

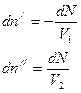Поэтому концентрация молекул в сосудах I и II через время 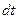станут равными:

.

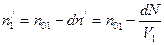
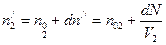Следовательно, разность концентраций станет равной:

.

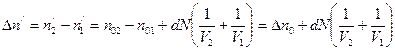Поставив в это выражение значение 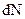из (4.7), получим:

.

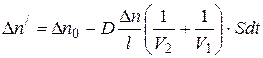Отсюда следует, что изменение концентрации за время 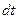равно:

.

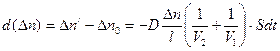Величину 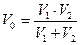называют приведенным объемом. Следовательно,

.

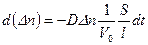Разделяя переменные, имеем:

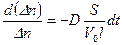. (4.8)

После интегрирования (4.8), получим:

.

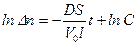С - постоянная интегрирования. Последнее выражение можно переписать в виде:

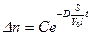. (4.9)

Постоянную интегрирования С легко найти, если известна начальная разность концентраций 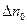в момент времени 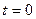. Подставляя эти условия в (4.9), получим:

.

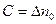Тогда

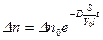. (4.10)

Согласно формуле (4.10) разность концентраций убывает со временем по экспоненциальному закону и тем быстрее, чем больше значение величины 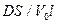, которое для данного опыта является постоянной величиной. Величина 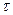, обратная этой постоянной 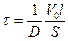, имеет размерность времени. При времени 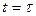разность концентраций 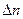становится равной 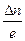, т.е. уменьшается в 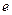раз по сравнению с начальной. Уравнение (4.10) можно переписать:

.

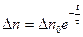Теплопроводность газов

Пусть в некотором объеме газа температура Т убывает в направлении оси Х, т.е. 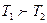(рис.11). Поскольку кинетическая энергия молекулы определяется как 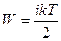, 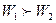. Поэтому в сторону убывания температуры будет происходить преимущественный перенос энергии, следовательно, и теплоты. В случае данной задачи переносимый молекулами физической характеристикой является

кинетическая энергия, т.е. 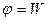. Будем считать, что 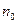одинакова во всем объеме. Тогда величины, входящие в уравнение переноса, выразятся следующим образом:

,

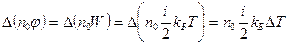где ,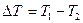

.

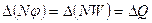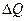- количество внутренней энергии, переносимое за время 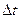через площадку 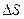перпендикулярно направлению переноса. Подставляя эти выражения в уравнение переноса (4.3), получим:

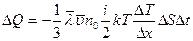. (4.11)

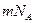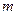Умножив числитель и знаменатель уравнения (4.11) на , где -масса молекулы, 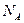-число Авогадро и учитывая, что 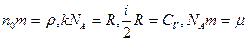, перепишем (4.11) в виде:

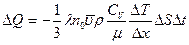, (4.12)

где 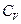-молярная теплоемкость при постоянном объеме, 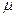-молярная масса. Так как 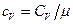-удельная теплоемкость, из (4.11) окончательно получим уравнение теплопроводности:

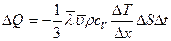. (4.13)

Эмпирически явление теплопроводности описывалось уравнением Фурье

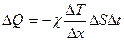, (4.14)

где 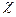называется коэффициентом теплопроводности. Из (4.13) и (4.14) следует, что выражение для коэффициента теплопроводности имеет вид:

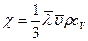. (4.15)

Рассмотрим зависимость коэффициента теплопроводности от давления и температуры. Из входящих в (4.15) величин, только плотность 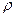и длина свободного пробега 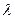зависят от давления, причем 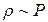и 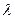~ 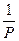. Это приводит к заключению, что коэффициент теплопроводности не зависит от давления. Этот вывод находится в превосходном согласии с опытными данными, которые показывают, что при изменении давления в широких пределах коэффициент теплопроводности остается постоянной.

Из величин, входящих в коэффициент теплопроводности (4.15), только одна величина 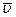зависит от температуры, причем 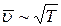, соответственно .

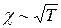Как показывает опыт, коэффициент теплопроводности растет с температурой несколько быстрее, чем 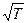. Это связано с тем, что коэффициент теплопроводности зависит от длины свободного пробега. Как показали раньше, 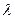не является постоянной величиной, а растет с температурой.