Вычисление дирекционных углов, румбов сторон теодолитных ходов и горизонтальных проложений их сторон
По исходному дирекционному углу aпп12-1и примычному горизонтальному углу bпр между ходом привязки и стороной замкнутого теодолитного хода 1– 2, вычисляют дирекционный угол стороны 1– 2:
a1-2 = aпп12 +180° - bпр.
Дирекционные углы последующих направлений находят по формуле:
an+1 = an + 180° - bn+1.
т. е. дирекционный угол последующей стороны теодолитного хода равен дирекционному углу предыдущей стороны плюс 180° и минус правый по ходу исправленный горизонтальный угол.
Контролем правильности вычисления дирекционных углов сторон является получение исходного дирекционного угла линии 1– 2.
Значения всех дирекционных углов записывают в графу 5 (таблица 4).
В примере:
a1-2 = aпп12 +180° - bпр.= 46˚24 ́+180˚ – 131˚ 26 ́= 94˚58 ́ ,
a2-3 = a1-2 + 180° - b2 = 94˚58 ́ + 180˚ – 106˚222́ = 118˚36́.
В конце вычислений получен дирекционный угол стороны 1– 2:
a1-2= 94˚58́.
Таблица 4
Ведомость вычисления координат
| № точки | Изме-ренн. углы | Поп-рав-ки | Исправлен-ные углы | Дирекцион-ные углы или азимуты | Румбы Название | Горизонт. проложе-ние, м | Приращения координат | Координаты | ||||||||
| вычисленные | исправленные | |||||||||||||||
| ° ¢ | ° ¢ | ° ¢ | ° ¢ | ±DХ | Поп-равка | ±DУ | Поп-равка | ±DХ | ±DУ | ±Х | ±Y | |||||
| Ход привязки от п.12 к точке №1 основного хода | ||||||||||||||||
| (12) | +175,54 | +98,50 | ||||||||||||||
| 46˚ 24́ | СВ:46˚ 24́́ | 157,24 | +108,43 | +113,87 | +108,43 | +113,87 | ||||||||||
| 131˚26́́ | 131˚ 26́ | +289,41 | +206,93 | |||||||||||||
| (2) | 94˚ 58́ | |||||||||||||||
| Основной замкнутый ход | ||||||||||||||||
| 89˚ 16́ | 89˚16 ́ | +289,41 | +206,93 | |||||||||||||
| 94˚ 58́ | ЮВ:85˚ 02́́ | 265,11 | -22,93 | 0,06 | +264,05 | +0,10 | -22,37 | +264,15 | ||||||||
| Продолжение таблицы 4 | ||||||||||||||||
| 106˚22́́ | 106 ˚22́́ | +266,54 | +471,08 | |||||||||||||
| 118˚ 36́́ | ЮВ:11˚ 24́́ | 204,66 | -200,57 | 0,04 | +40,32 | +0,08 | -200,53 | +40,40 | ||||||||
| 122˚ 42́́ | +1 | 122˚ 43́ | +66,01 | +511,48 | ||||||||||||
| 225˚ 53́́ | ЮЗ:45˚53́́ | 157,88 | -110,52 | 0,03 | -112,73 | +0,06 | -110,49 | -112,67 | ||||||||
| 105˚ 13́́ | +1 | 105˚ 14́ | -44,48 | +398,81 | ||||||||||||
| 300˚ 39́́́ | СЗ:59˚21́́ | 241,25 | +122,97 | 0,05 | -207,48 | +0,09 | +123,02 | -207,39 | ||||||||
| 116˚ 25́́́ | 116 ˚25́́ | +78,54 | +191,42 | |||||||||||||
| 4˚ 14́́́ | СВ:4˚14́́ | 211,46 | +210,83 | 0,04 | +15 44 | +0,07 | +210,87 | +15,51 | ||||||||
| (1) | 94˚ 58́́́ | +289,41 | +206,93 | |||||||||||||
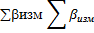 | 539˚ 58́́́ | 540 ˚00́́́ | Р=1080,30 | å+ 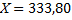 | 0,22 | å+ 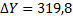 1 1 | -0,40 | å+ 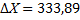 | å+ 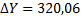 | |||||||
| åbтеор | 540˚ 00́́ | å- 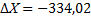 | å- 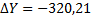 | å- 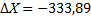 | å- 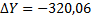 | |||||||||||
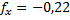 | 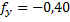 | 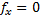 | 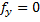 | |||||||||||||
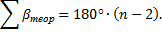 fb = åbизм – åbтеор = 539°58¢ – 540°00¢ = −2¢ fbдоп = ± 1,5×t Ön = ±1,5×1Ö5 = ± 3,35¢ fb = åbизм – åbтеор = 539°58¢ – 540°00¢ = −2¢ fbдоп = ± 1,5×t Ön = ±1,5×1Ö5 = ± 3,35¢ | fАБС = Ö fx 2 + fy 2 = Ö0,222 + 0,402 @ 0,45 м. fотн= 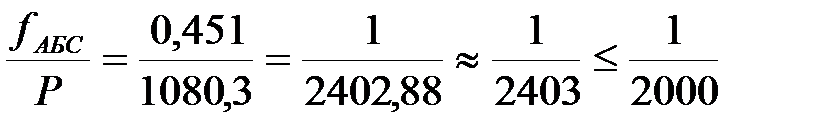 | |||||||||||||||
Продолжение таблицы 4
| № точки | Измереннуглы | Поп-рав-ки | Исправлен-ные углы | Дирекцион-ные углы или азимуты | Румбы | Горизонт проложе-ние, м | Приращения координат | Координаты | |||||||||
| вычисленные | исправленные | ||||||||||||||||
| ° ¢ | ° ¢ | ° ¢ | Назв.° ¢ | ±DХ | Поп-равка | ±DУ | Поп-равка | ±DХ | ±DУ | ±Х | ±у | ||||||
| Диагональный ход | |||||||||||||||||
| (5) | 4˚ 14́ | ||||||||||||||||
| 43˚10́́ | - | 43˚ 10́ | 141˚ 04́́ | ЮВ:38˚56́ | 194,41 | -151,64 | -0,05 | +122,08 | -0,08 | -151,69 | +122,00 | +289,41 | +206,93 | ||||
| 209˚38́ | 209˚ 39́ | +137,22 | +328,93 | ||||||||||||||
| 111˚ 25́́ | ЮВ:68˚35́ | 196,39 | -72,66 | -0,05 | +182,64 | -0,09 | -72,71 | +132,55 | |||||||||
| 65˚32́ | - | 65˚32́ | +65,01 | +511 48 | |||||||||||||
| (4) | 225˚ 53́ | ||||||||||||||||
| Окончание таблицы 4 | |||||||||||||||||
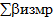 | 318˚ 20 | Р=390,80 | 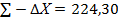 | -10 | å+ 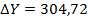 1 1 | -0,17 | å 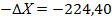 | å 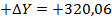 | |||||||||
| åbтеор | 318˚ 21 | ||||||||||||||||
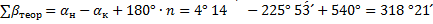 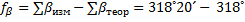 21 ́= - 1 ́ 21 ́= - 1 ́ 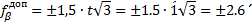 | 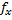 = = 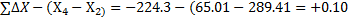 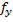 = = 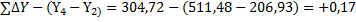 fАБС = Ö fx 2 + fy 2 = Ö0,12 + 0,172 @ 0,20 м fотн= fАБС = Ö fx 2 + fy 2 = Ö0,12 + 0,172 @ 0,20 м fотн= 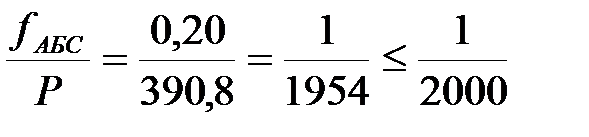 . . | ||||||||||||||||
Переводят дирекционные углы в румбы по зависимостям (табл. 5)
Таблица 5
Взаимосвязь румбов и дирекционных углов
| № четверти | Пределы четверти | Название румба | Зависимость |
| I | 0°-90° | CВ | r = a |
| II | 90°-180° | ЮВ | r = 180°- a |
| III | 180°-270° | ЮЗ | r = a - 180° |
| IV | 270°-360° | СЗ | r = 360°- a |
Вычисленные значения румбов записывают в графу 6 (табл.4).
Горизонтальные проложения сторон теодолитного хода d определяют по измеренным на местности длинам сторон Dср и углам наклона сторон к горизонту gпо формуле:
d = Dср×cosg.
Если углы наклона g < 2°, то горизонтальные проложения равны измеренным длинам сторон теодолитного хода.
В примере только сторона хода 3-4 имеет угол наклона более 2˚, поэтому:
a3-4 = 158,32 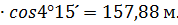
Вычисленные значения горизонтальных проложений d записывают в графу 7 (табл.4), после чего определяют периметр теодолитного хода:
Р = d1-2 + d2-3 + …….. + dn – n+1.
