Автокорреляция в остатках, критерий Дарбина-Уотсона в оценке качества уравнения тренда

Зависимость между последовательными уровнями врем. ряда называют автокорреляцией уровня ряда. Автокорреляция в остатках –это корреляционная зависимость между значениями остатков за текущий и предыдущий моменты времени.

Один из наиболее распространенных методов определения автокорреляции в остатках – критерий Дарбина-Уотсона:

d = ;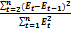

d – отношение суммы квадратов разностей последовательных значений к остаточной сумме квадратов по модели регрессии.

Сущ-ет след. соотношение между критерием Д-У «d» и коэф-ом автокорреляции остатков 1ого порядка r₁:

d = 2 * (1-r₁) .

Если в остатках сущ-ет полная положит. автокорреляция и r₁ = 1, то d = 0.

Если в остатках полная отриц. автокорреляция, то r₁ = -1 и d = 4.

Если автокорреляция отсутствует, то r₁ = 0 и d = 2.

Т.е. 0≤d≤4.

Рассмотрим алгоритм выявления автокорреляции остатков на основе критерия Д-У.

Выдвигается гипотеза H₀ об отсутствии автокорреляции остатков. Альтернативные гипотезы H₁ и H₁^* предполагают наличие положительной или отрицательной автокорреляции в остатках. Затем по спец. таблицам определяютсякритические значения критерия Дарбина — Уотсона d_L и d_u для заданного числа наблюдений n, числа независимых переменных модели k при уровня значимости ɑ (обычно 0,95). По этим значениям промежуток [0;4] разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью (1-ɑ) представлено на след: рисунке:

Есть положит. автокорреляция остатков. Н0 отклоняется. С вер-тью Р=1-ɑ принимается Н1.

Зона неопределенности.

Нет оснований отклонять Н0 (автокорреляция остатков отсутствует).

Зона неопределенности.

Есть отриц. автокорреляция остатков. Н0 отклоняется. С вер-тью Р=1-ɑ принимается Н1.

dL

du

4- du

4- dL

+ есть	?	НЕТ	?	- есть
	dL	du		4- du	4- dL

Если фактич. значение критерия Дарбина - Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и гипотезу Н₀ отклоняют.

Ограничения на применение критерия Дарбина-Уотсона :

1. Неприменимость к модели авторегрессии;

2. Использование для выявления автокорреляции остатков 1ого порядка;

3. Возможность получения достоверных результатов только для больших выборок.

45. Анализ временных рядов при наличии периодических колебаний: аддитивная имультипликативная модели.

Известно несколько подходов к анализу структуры временных рядов, содержащих сезонные и циклические колебания. Моделирование циклических колебаний осуществляется аналогично моделированию сезонных колебаний.

Простейший подход-это расчет значений сезонной компоненты методом скользящей средней и построение аддитивной и мультипликативной модели временного ряда.

Модель в кот временный ряд представлен как сумма перечисленных компонент называется аддитивной моделью, как произведение перечисленных компонент- мультипликативной моделью.

Аддитивная: Y=T+S+E

Мультипликативная: Y=T*S*E

данная модель предполагает, что каждый уровень временного ряда может быть представлен как сумма или произведение трендовой(T), циклической(S) и случайной(Е) компонент.

Выбор одной из двух моделей производится на основе анализа структуры сезонных колебаний.

Если амплитуда колебаний приблизительно постоянна, то строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянно для различных циклов.

Если амплитуда сезонных колебаний возрастает и уменьшается, то строят мультипликативную модель, кот ставит уровни ряда в зависимость от значений сезонной компоненты.

Построение модели включает следующие шаги:

-выравнивание исходного ряда методом скользящей средней
-расчет значений сезонной компоненты
-устранение сезонной компоненты из исходных уровней ряда, получение выровненных данных (T+E) в аддитивной или (Т*Е) в мультипликативной модели
-аналитическое выравнивание уровней (T+E) или (T*E) и расчет значений Т с использованием полученного уравнения тренда.
-расчет полученных по модели значений (T+S) или (T*S)
-расчет абсолютных и/или относительных ошибок

Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уравнения ряда и в дальнейшем использовать временной ряд ошибок для анализа взаимосвязи исходного ряда и других временных рядов.

46. Применение фиктивных переменных для моделирования сезонных колебаний.

Количество фиктивных переменных в модели должно быть на единицу меньше числа периодов времени внутри одного цикла колебаний. Например при моделировании по кварталам, данная модель должна включать четыре независимые переменные- фактор времени при фиктивной переменной.

Каждая фиктивная переменная отражает сезонную компоненту временного ряда какого-либо одного периода. Она равна 1 для данного периода и 0 для всех остальных периодов.

Пусть имеется временной ряд, содержащий циклические колебания периодичностью К.
Модель регрессии с фиктивными переменными для этого ряда будет иметь вид:

Y₁=a+bt+c₁x₁+…+c_jx_j+…+c_k-1x_k-1+E (1)

Где x_j=1 для для каждого j внутри каждого цикла, x_j=0 во всех остальных случаях

Например при моделировании сезонных колебаний на основе поквартальных данных за несколько лет, число кварталов внутри каждого года К равно 4.

Yt=a+bt+c₁x₁+c₂x₂+c₃x₃+Et (2)

Где x₁=1 для первого квартала, x₁=0 для остальных
x₂=1 для второго квартала, x₂=0 для ост
x₃=1 для третьего картала, x₃=0 для остальных.

Уравнение тренда для каждого квартала будет иметь вид:

I: Yt=a+bt+c₁+E_t
II: Yt=a+bt+c₂+E_t
III: Yt=a+bt+c₃+E_t
IV: Yt=a+bt+E_t

Таким же образом фиктивная переменная позволяет дифференцировать величину свободного члена уравнения регрессии. Для каждого квартала она составит:

I: a+c₁
II: a+c₂
III: a+c₃
IV: a (3)

Параметр b в модели (3) характеризует среднее абсолютное изменение уровней ряда под воздействием тенденции. В сущности модель (2) есть аналог аддитивной модели временного ряда, поскольку фактический уровень временного ряда это сумма трендовой, сезонной и циклической компонент.

47. Особенности изучения взаимосвязанных временных рядов.

Изучение причинно-следственных зависимостей переменных, представленных в форме временных рядов, является одной из самых сложных задач эконометрического моделирования.

Применение традиционных методов корреляционно-регрессионого анализа (КРА) может привести к серьёзным проблемам.

Необходимо сначала изучить структуру временного ряда и устранить сезонную или циклическую компоненту их уровня ряда, если они выявлены. Поскольку её наличие приведёт к завышению истинных показателей силы и тесноты связи изучаемых временных рядов в случае, если оба ряда содержат циклические колебания одинаковой периодичности, либо к занижению этих показателей случае, если сезонные, или циклические, колебания содержат только один из рядов или если периодичность колебаний в рассматриваемых временных рядах различна.

48. Автокорреляция по рядам динамики и методы ее устранения.

Предположим, что по двум временным рядам x_t и y_t строится уравнение парной линейной регрессии вида

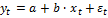
Наличие тенденции в каждом из этих временных рядов означает, что на зависимую y_t и независимую x_t переменные модели оказывает воздействие фактор времени, который непосредственно в модели неучтён.

Влияние фактора времени будет выражено в корреляционной зависимости между значениями остатков 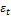за текущий и предыдущий моменты времени, которая получила название автокорреляция в остатках.

Автокорреляция в остатках – это нарушение одной из основных предпосылок МНК – предпосылки о случайности остатков, полученных по уравнению регрессии.

Автокорреляция в остатках может быть вызвана:

1. Ошибками измерения при первоначальном сборе данных по результативному признаку;

2. Неправильно выбранной формулировкой исходной модели; при формировании модели может быть упущен из вида фактор, оказывающий существенное влияние на результат. В итоге влияние этого фактора отражается в остатках в виде их автокорреляции. Часто этим фактором выступает показатель времени.