Современное состояние проблемы моделирования систем
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Коломенский институт (филиал)
Государственного образовательного учреждения высшего профессионального образования
«Московский государственный открытый университет»
В.М. КАШИН, В.Г. НОВИКОВ
ОСНОВЫ ТЕОРИИ И ПРАКТИКИ МОДЕЛИРОВАНИЯ ДИНАМИЧЕСКИХ СИСТЕМ
Учебное пособие
Коломна 2011
УДК 519.8 (076)
ББК 22.18
М–74
Рецензенты:
- доктор технических наук, профессор ТРУШКОВ А.С. (Московский государственный областной социально-гуманитарный институт (МГОСГИ), Коломна Московской области);
- кандидат технических наук, профессор МЯЛЬДЗИН Н. Х. (Коломенский институт МГОУ, Коломна Московской области);
- кафедра “Автоматики и электроники в машиностроении” Коломенского института МГОУ (Коломна Московской области).
Авторами пособия являются:
- действительный член РАРАН, доктор технических наук, заведующий кафедрой "Информатики и информационных технологий" КИ МГОУ Кашин В.М.;
- доктор технических наук, профессор кафедры “Автоматики и электроники в машиностроении” КИ МГОУ Новиков В.Г.
Основы теории и практики моделирования динамических систем:Учебное пособие/ Кашин В.М., Новиков В.Г. – Коломна: КИ МГОУ, 2011. – 215 с., ил.
В учебном пособии излагаются основы теории и практики моделирования динамических систем. Отдельным разделом даны приемы создания моделей в среде инженерных приложений Simulink программного продукта Matlab.
Содержание соответствует Государственным образовательным стандартам высшего профессионального образования по направлению подготовки дипломированного специалиста 220000 – “Автоматика и управление” и бакалавра 220200 – “Автоматизация и управление”.
Для студентов очной и очно-заочной формы обучения по специальности 220201 - Управление и информатика в технических системах, по направлению 220200 - Автоматизация и управление.
Утверждено Учебно-методическим Советом Коломенского института МГОУ, Председатель Совета Липатов А.М.
УДК 519.8 (076)
ББК 22.18
© Кашин В.М., Новиков В.Г.
© КИ МГОУ, 2010
СОДЕРЖАНИЕ
Введение. 7
1. Современное состояние проблемы моделирования систем. 10
1.1. Моделирование как метод научного познания. Философские аспекты моделирования. 10
1.2. Использование моделирования при исследовании и проектировании систем 11
1.2.1. Особенности разработки систем. 11
1.2.2. Особенности использования моделей. 11
1.2.3. Перспективы развития методов и средств моделирования систем. 11
2. Основные понятия теории моделирования систем. 13
2.1. Принцип системного подхода в моделировании систем. 13
2.1.1. Структура системы – совокупность связей между элементами системы.. 13
2.1.2. Экспериментальные исследования систем. 14
2.2. Стадии разработки моделей. 14
2.3. Понятие подобия. 14
2.3.1. Общие положения. 14
2.3.2. Основные понятия теории размерности. 15
2.3.3. Примеры подобия. 18
2.4. Общая характеристика проблемы моделирования систем. 21
2.4.1. Объект моделирования. 21
2.4.2. Характеристики моделей систем. 21
2.4.3. Цели моделирования систем. 22
2.5. Классификация видов и методов моделирования систем. 23
2.5.1. Классификационные признаки. 23
2.5.2. Математическое моделирование. 24
2.6. Построение модели. 27
2.7. Разработка вычислительного метода. 27
2.8. Проверка (тестирование) модели. 27
3. Математическое моделирование. 29
3.1. Задачи и цели исследования математических моделей. 29
3.2. Методология математического моделирования. Системный анализ 29
3.2.1. Понятие системы.. 29
3.2.2. Этапы системного анализа и декомпозиция. 30
3.2.3. Экспертные оценки. 32
3.3. Классификация математических моделей. 33
3.4. Методы формализованного описания системы.. 34
3.4.1. Математическая модель по “входу-выходу”. 35
3.4.2. Математическая модель в пространстве состояний. 35
3.4.3. Описание линейных систем в пространстве состояний. 35
3.4.4. Реализация систем в пространстве состояний. 37
3.5. Методы построения математических моделей и их применение в САПР. 39
3.5.1. Методы построения математических моделей. 39
3.5.2. Математические модели с точки зрения САПР. 41
3.5.4. Методика составления уравнений динамики элементов САУ.. 47
3.6. Математические модели системы управления. Понятие об оптимальном управлении. 49
4. Экспериментальное определение динамических характеристик объектов моделирования. 52
4.1. Понятие о динамических характеристиках объектов. 52
4.2. Определение динамических характеристик элементов систем по временным характеристикам. 52
4.2.1. Определение статических характеристик. 53
4.2.2. Определение динамических характеристик объектов с помощью периодических воздействий. 56
4.4.1. Временные характеристики и их свойства. 58
4.4.2. Определение характеристик апериодического звена. 59
4.4.3. Определение характеристик колебательного звена. 59
4.3. Формы описания динамических свойств объектов. 60
4.4. Синтез пассивных двухполюсников и четырехполюсников. 61
4.3.1. Разложение передаточной функции активного четырехполюсника. 62
4.3.2. Способы синтеза двухполюсников. 63
4.5. Экспериментальная отработка характеристик системы управления движущимся объектом. 66
4.5.1. Общие положения. 66
4.5.2. Алгоритмы обработки внешнетраекторных измерений. 67
5. Динамические свойства воспринимающих элементов и датчиков. 71
5.1. Основные определения и понятия. 71
5.1.1. Понятие датчика. 71
5.1.2. Классификация датчиков. 72
5.2. Основные характеристики датчиков. 73
5.2.1. Погрешности измерений. 73
5.2.2. Чувствительность датчиков. 74
5.2.3. Быстродействие датчика. 76
5.3. Схемы формирования сигналов пассивных датчиков. 77
5.3.1. Общие характеристики. 77
5.3.2. Потенциометрические схемы датчиков. 78
5.4. Оптические датчики. 79
5.4.1. Определения и основные зависимости. 79
5.4.2. Фоторезисторы.. 80
5.4.3. Фотодиоды.. 81
5.4.4. Тепловые приемники излучения. 81
5.4.5. Датчики изображения. 81
5.4.6. Волоконная оптика. 81
5.5. Датчики температуры.. 81
5.5.1. Методы измерения температуры.. 81
5.5.2. Шкалы температур. 82
5.6. Датчики положения и перемещения. 82
5.6.1. Методы определения положения и перемещения. 82
5.6.2. Резисторные потенциометры.. 82
5.6.3. Индуктивные датчики. 83
5.6.4. Емкостные датчики. 84
5.6.5. Цифровые датчики. 86
5.6.6. Датчики близости. 86
5.7. Датчики деформации. 87
5.7.1. Основные определения. 87
5.7.2. Основные положения. 87
5.8. Тахометрические датчики. 89
5.8.1. Электродинамическая тахометрия. 89
5.8.2. Импульсная тахометрия. 89
5.8.3. Гирометры.. 90
5.9. Датчики ускорения, вибрации и удара. 91
5.9.1. Общие положения. 91
5.9.2. Принцип действия сейсмических датчиков. 91
5.10. Датчики скорости, расхода и уровня жидкости. 95
5.10.1. Элементарные понятия. 95
5.10.2 Датчики и методы измерения скорости жидкости. 98
5.10.3. Измерение расхода жидкости. 101
5.10.4. Измерение и указание уровня жидкости. 106
5.11. Датчики влажности. 107
5.11.2. Гигрометры.. 107
5.12. Акустические датчики. 108
5.12.1. Распространение плоской волны.. 109
5.12.3. Микрофоны.. 111
5.12.4. Измерение интенсивности. 119
6. Основы технологии имитационного моделирования. 120
6.1. Основные определения и понятия. 120
6.2. Область применения и классификация имитационных моделей. 120
6.3. Описание поведения системы.. 121
6.3.1. Общие положения. 121
6.3.2. Методика моделирования случайных факторов. 121
6.3.3. Два подхода к моделированию случайных чисел. 122
6.4. Оценка качества псевдослучайных чисел. 123
6.5. Оценка качества имитационного моделирования. 124
7. Методы испытаний систем управления и их применение в системах автоматизированного проектирования (САПР) 125
7.1. Полунатурное моделирование. 125
7.1.1. Общие положения. 125
7.1.2. Автоматизация испытаний на основе полунатурного моделирования. 126
8. Анализ систем управления с ЭВМ.. 129
8.1. Основные задачи. 129
8.2. Особенности систем управления с ЭВМ.. 130
8.2. Основные положения из теории дискретных линейных систем. 131
8.2.1. Последовательности. 131
8.2.2. Линейные системы с постоянными параметрами. 132
8.2.3. Разностные уравнения. 133
8.2.4. Z – преобразование. 135
8.3. Расчет цифровых фильтров по фильтрам непрерывного времени. 138
8.3.1 Методика синтеза цифровых фильтров. Общие положения. 138
8.3.2 Методы дискретизации аналоговых фильтров. 140
8.3.3. Геометрическая интерпретация методов расчета цифровых фильтров по фильтрам непрерывного времени. 141
9. Моделирование свойств объектов с помощью системы MatLab. 144
9.1. Введение. 144
9.2. MatLab как научный калькулятор. 144
9.2.1. Командное окно. 144
9.2.2. Операции с числами. 145
9.2.3. Простейшие операции с векторами и матрицами. 146
9.2.4. Некоторые функции прикладной численной математики. 147
9.2.5. Построение простейших графиков. 149
9.3. Исследование линейных стационарных систем (ЛСС) 150
9.3.1. Классы пакета CONTROL.l 150
9.3.2. Ввод и преобразование моделей. 151
9.3.3. Анализ системы.. 155
9.4. Моделирование динамических процессов с помощью подсистемы MatLab SIMULINK.. 158
9.4.1. Краткие сведения о подсистеме MatLab SIMULINK.. 158
9.4.2. Запуск подсистемы SIMULINK.. 158
9.4.3. Создание модели. 159
9.4.4. Некоторые основные приемы подготовки и редактирования модели. 160
9.4.5. Установка параметров моделирования и его выполнение. 161
9.2.2. Результат составления модели. 164
Приложения. 165
П1. Динамические характеристики объектов моделирования. 165
П2. Примеры составление функциональной и структурной схемы динамической системы.. 169
П2.1. Система управления угловой скорости вращения ротора двигателя при условии действия постоянного возмущения. 169
П2.2. Система сопровождения цели. 170
П2.3. Система автоматического наведения летательного аппарата на объект 171
П2.4. Система управления уровнем жидкости. 174
П2.5. Система управления экономическими параметрами. 175
Использованные источники. 177
Введение
Дисциплина “Моделирование систем“ – особая наука. Она занимает достойное и важное место в теории познания – в гносеологии.
Под системой понимается совокупность взаимодействующих элементов, упорядоченная для достижения одной или нескольких поставленных целей [8].
У каждого из заказчиков, разработчиков, производителей и пользователей сложных систем (любой области приложения), служб обеспечения качества и безопасности и др. рано или поздно неизбежно возникают принципиальные системные вопросы. Например:
“Как достичь уровня международных стандартов?” (понимая под этим высокий уровень качества и конкурентоспособности производимой продукции);
“Достижимы ли ожидаемые эффекты?” (для разработчика особенно важно понять, на что все-таки реально они могут рассчитывать по завершении проекта в пределах выделенных ресурсов);
“Выполнимы ли задаваемые требования?”;
“Насколько безопасны те или иные сценарии?”;
“Какие меры более эффективны?” (понимая, что критерием может выступать либо максимум выигрыша (прибыли, качества, безопасности), либо минимум затрат (ущерба) при соответствующих ограничениях) и др.
Поскольку подобные вопросы возникают на протяжении всего жизненного цикла системы, у любых специалистов возникает естественное желание опереться в своих усилиях на успешный опыт коллег.
Практика доказала невозможность всесторонних испытаний за приемлемое время. Это объясняется, в первую очередь, объемностью проверок функционирования программного обеспечения при многочисленных сценариях его использования. Следствием является существенное возрастание роли моделирования как наиболее эффективного гаранта всесторонней оценки эффективности создаваемой системы.
Математическое моделирование - важнейший наукоемкий процесс в сопровождении создания и эксплуатации сложных систем, позволяющий оценить вероятности успеха, риски, прибыли и ущербы. В результате адекватного моделирования углубляются и расширяются знания о системе, о возможности результатов от различных характеристик самой системы и условий ее создания и функционирования, наконец, о степени достижения целей, которые стоят перед системой.
Моделирование – это стремление к истине. Исследователь, познавая мир, всегда исходит из различных предположений. Достигнув определенного уровня, он создает, таким образом, мысленно или материально модель исследуемого объекта.
Достигнув определенной цели, познав суть явления, он обретает знания. Однако, это знание относительное, не абсолютное. Оно верно лишь при заданных допущениях.
Далее исследователь усложняет себе задачу: а что будет, если мы снимаем то или иное ограничение, исключим такое-то допущение?
Создается модель другого уровня и т.д.
Поэтому можно смело заявить, что моделирование – один из способов, методов поиска истины.
В любой сфере человеческого бытия, его деятельности мы всегда, каждодневно и неминуемого сталкиваемся с моделированием – на производстве ли, в общественной жизни или в быту…
Идет ли человек к своим подчиненным или на прием к начальству – он всегда предварительно моделирует свою поведенческую линию. При этом в каждом случае модели бывают разные.
Или понаблюдаем поведение студента до и после экзамена.… Оно отличается. И каждый знает, поведение зависит от результата…
Или вот пример. Хозяйка встречает дома на кухне члена своей семьи или гостя. В каждом случае модели ее поведения разные…
Взрослый разговаривает с малышом или ведет беседу со взрослым – модели поведения также различные…
Налицо зависимость линии поведения от множества внешних факторов.
Научный сотрудник, инженер-конструктор проводит исследования, проектирует, допустим, ракетный комплекс, и ему необходимо определить границы зон на местности, находиться в которых при проведении стрельб опасно для жизни - зоны риска. Для расчета таких зон создается модель движения ракеты в воздушном пространстве. Размеры этих зон зависят от многих факторов, параметров, которые учитываются при создании модели. Кроме того, их размеры будут различны зимой, летом, зависят от барометрической высоты.
Таким образом, размеры опасной зоны (как обобщенный параметр, ее площадь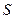 
) являются функцией вектора 
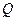множества параметров и факторов 
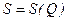. Причем проявление факторов является в общем случае случайной величиной случайной функции. Отсюда следует, что размеры зон также носят случайный характер.
Задача исследователя в данном случае заключается свести к минимуму количество неучтенных факторов и максимально достоверно определить вероятность проявления тех или иных размеров зон риска.
Общеизвестно определение науки как инструмента исследования явлений в природе, обществе строго определенными методами, в основе которых лежит установление причинно-следственных связей между явлениями. В соответствии с этим определением моделирование можно отнести к науке.
В целом теория моделирования – прикладная наука. И она предполагает, что изучающий эту науку владеет знаниями в области ряда остальных наук: математики, физики, химии, теории автоматического управления, теории вероятности, электротехники, философии и др. В целом, образно можно считать, что место этой науки на вершине дерева, корнями которого являются перечисленные отрасли наук.
Особое место при исследовании, изучении теории моделирования занимает теория автоматического управления. Поэтому в данном курсе под системой часто подразумевается система автоматического управления, поскольку практически все устойчивые явления можно свести формально к замкнутой системе автоматического управления. И предметом исследования при выполнении лабораторных работ в пределах данного курса будут некие системы автоматического управления.
Уместно здесь выделить еще один момент.
Любая наука и (или) учебная дисциплина начинаются с научного “языка”, характерного для данной предметной области. Как правило, такой научный “язык” включает область основных понятий, определений, задач соответствующей области человеческого знания. Очевидно, что, не определив сразу эти понятия, нельзя переходить к конкретным, детальным вещам, так как мы (ученики и учителя, разработчики и заказчики техники и систем, научные учреждения и учебные заведения, студенты и преподаватели) просто не поймем друг друга. Более того, продвижение по пути научно-технического прогресса невозможно без учета реальной обстановки, сложившейся в плане информационного обмена в широком смысле (например, свыше 90% всей научной литературы издается на 6 языках), а также в рамках конкретной теории [7].
Заметим, что большинство научно-практических достижений в мире совершаются на этих языках. Они лаконичны, а это очень важно для науки. Явление в отдельных независимых государствах бывшего СССР, распространенное в 90-х годах 20-го столетия, связанное с искусственным переводом научно-технической, физико-математической литературы на свои языки в угоду политическим амбициям лидеров этих государств, пагубно сказывается на качестве образования, на производстве.
При изучении дисциплины “Моделирование систем“ мы вынуждены общаться на нескольких языках. Поскольку данная дисциплина опирается на ряд наук, то и в качестве таких научных языков, как базы для успешного изучения дисциплины, выступают все теории, на которые опирается та или иная из перечисленных выше наук.
Таким образом, теория моделирования систем является сложнейшей наукоемкой дисциплиной, опирающейся на самые современные разделы ряда наук.
Данное учебное пособие предназначено дать представление о методах и способах моделирования технических систем. Задачей курса является овладение методами составления математических моделей систем различных классов, овладение методами анализа моделей таких систем. Также в задачу курса входит овладение практическими навыками составления и исследования моделей. При этом даются основы системы программирования MatLab, как наиболее широко используемой в инженерных и научных исследованиях, и которая послужила в пределах данного курса инструментом для выполнения лабораторных работ.
В пособии предметом изучения теории моделирования являются современное состояния проблемы моделирования систем, основные понятия теории моделирования, принципы системного подхода и подобия.
Достаточно широко рассмотрены основы математического моделирования, классификации видов такого моделирования. Рассмотрены основные свойства и отличия математических моделей в пространстве состояний и моделей по “входу и выходу”.
Даны основы экспериментального определения динамических характеристик объектов моделирования.
Отдельная глава посвящена достаточно подробному изучению динамических свойств широкого класса воспринимающих элементов и датчиков, принцип действия которых основан на различных законах физики.
Даются основы технологии имитационного моделирования, полунатурного моделирования, рассмотрены методы испытаний систем.
Отдельно уделено внимание анализу систем с использованием ЭВМ, использование которых необходимо предполагает рассмотрение класса дискретных систем, описываемых разностными уравнениями. Представлены некоторые методы расчета цифровых фильтров по известным фильтрам непрерывного времени.
В приложении приведены отдельные примеры составления функциональной и структурной схем динамических систем различной природы.
Современное состояние проблемы моделирования систем