Вопрос 7.5. Формула Тейлора с остаточным членом в интегральной форме

Теорема 7.5. Если 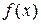имеет непрерывную 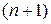‑ю производную на отрезке 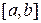, то справедлива формула Тейлора с остаточным членом в интегральной форме

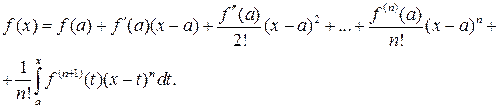
Доказательство. По формуле Ньютона – Лейбница, интегрируя по частям n раз, получим

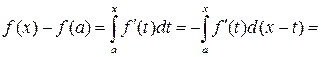
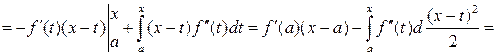
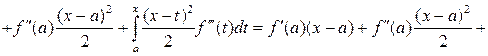
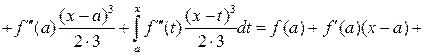
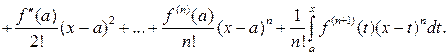
Конец доказательства.

ЛЕКЦИЯ № 8. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Вопрос 8.1. Формула трапеций.

Теорема 8.1. (Обобщенная теорема о среднем значении). Пусть функция 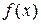непрерывна на отрезке 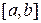, а функция 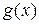интегрируема и неотрицательна ( 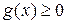) на этом отрезке. Тогда справедлива формула

,

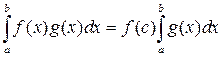где c принадлежит отрезку .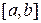

Доказательство. Так как 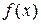непрерывна на 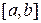, то она достигает своего минимального и минимального значения на этом отрезке. Пусть m ‑ минимальное, а M ‑ максимальное значения функции на отрезке 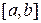. Тогда 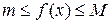. Интегрируя это неравенство, умноженное на функцию 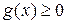, получим

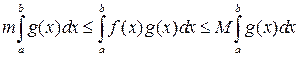
или

.

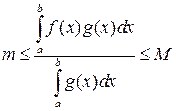Интеграл 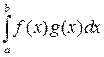существует, так как произведение интегрируемых функций является интегрируемой функцией. В силу непрерывности функции 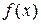всегда найдется точка c, в которой достигается указанное промежуточное значение между m и M. Следовательно

.

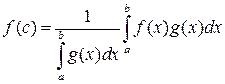Конец доказательства.

Теорема 8.2. (Формула трапеций). Если 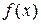имеет непрерывную вторую производную на отрезке 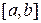, то справедлива формула

,

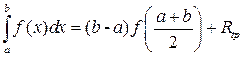где 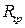‑ остаточный член формулы трапеций, равный

.

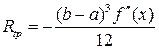Пояснение. Так как (см. рис. 1)

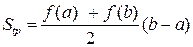
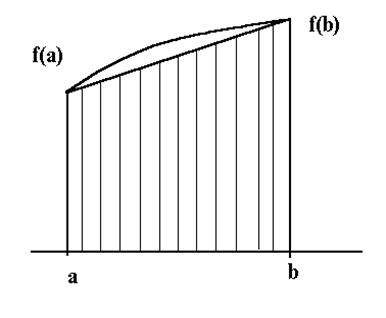
Рис. 1. Формула трапеций.

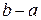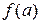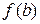есть площадь трапеции, высотой и основаниями и , то смысл формулы состоит в том, что значение интеграла, равное площади криволинейной трапеции, равно площади обычной трапеции (для неотрицательных функций).

Доказательство. Используем формулу Тейлора с остаточным членом в интегральной форме

.

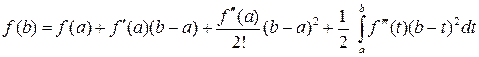Обозначим через 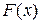функцию 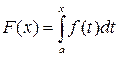, и разложим ее в ряд Тейлора

.

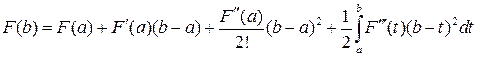Аналогично разложим функцию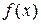

.

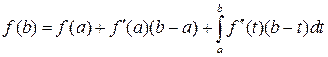Но 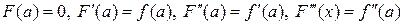. Пусть 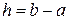, тогда

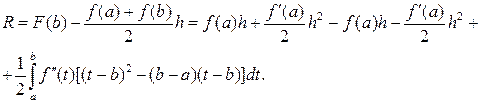
Откуда

.

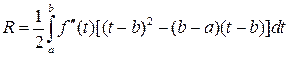Подынтегральная функция

,

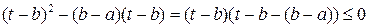тогда по обобщенной теореме о среднем значении получим

.

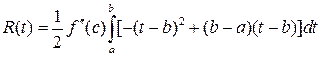Интегрируя, получим

.

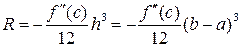Определение 8.1. Длины отрезков разбиения называются шагами интегрирования, а их концы называются узлами интегрирования. Формулы интегрирования называются составными или усложненными.

Рассмотрим усложненную формулу трапеций с постоянным шагом интегрирования h и узлами

.

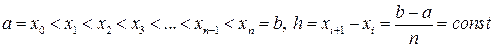Тогда

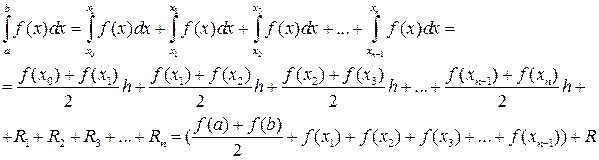
где

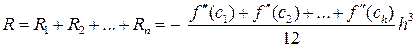
Пусть m ‑ минимальное, а M ‑ максимальное значение 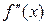на отрезке 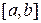. Тогда 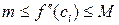. Складывая эти неравенства с 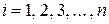, получим

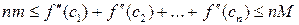
или

.

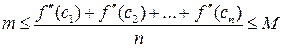В силу непрерывности 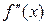пробегает все промежуточные значения от m до M, поэтому существует точка c, такая что

.

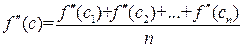Так как 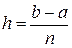, то

.

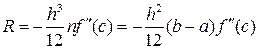Отсюда получим усложненную формулу трапеций

,

.
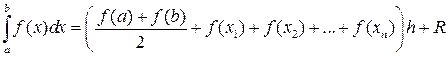
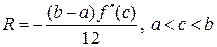