Уравнение постоянства расхода (уравнение неразрывности)

ГИДРОДИНАМИКА

Методы исследования движения жидкости

Гидродинамика − это раздел гидравлики, в котором изучаются общие законы движения реальной жидкости и ее взаимодействие с твердыми стенками.

Благодаря текучести жидкой среды отсутствуют жесткие связи между ее отдельными частицами, и общий характер движения оказывается более сложным, чем характер движения твердого тела.

Изучение движения жидкости представляет значительные сложности в силу того, что ее частицы обладают большой подвижностью и в общем случае в различных точках пространства и в различные моменты времени имеют различные скорости по величине и направлению.

При исследовании движения жидкости применяют два основных метода: Лагранжа и Эйлера.

При исследовании по методу Лагранжа рассматривается движение отдельных частиц вдоль их траекторий. Для этого замечают координаты 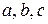в начальный момент времени 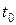. Все последующие координаты точки 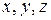и составляющие скорости 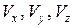будут зависеть от начальных координат, называемых переменными Лагранжа:

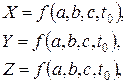
где 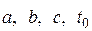− переменные Лагранжа.

Если параметры 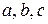зафиксированы, то приведенное выражение устанавливает кинематические характеристики конкретной жидкой частицы, аналогично тому, как определяют соответствующие характеристики материальной точки.

При изменении параметров 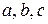осуществляется переход от одной жидкой частицы к другой и таким образом можно охарактеризовать движение всей конечной массы жидкости.

Метод Эйлера состоит в определении скорости и давления жидкости в той или иной точке неподвижного пространства, т. е. изучаются поля скоростей и давлений в некоторые последующие моменты времени. Таким образом, движение описывается уравнениями:

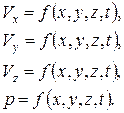
В гидравлике обычно применяется метод Эйлера, так как он относительно более прост, чем метод Лагранжа (решение уравнений по Лагранжу сложны и трудноразрешимы).

Основные понятия и определения гидродинамики

В гидродинамике также широко используют решения, полученные для идеальной жидкости, которые переносятся на реальную жидкость с внесением необходимых поправок на ее свойства, в первую очередь на вязкость и сжимаемость.

Движение жидкости определяется скоростью в отдельных точках, давлениями, возникающими на различных глубинах, глубинами, а также общей формой потока. Указанные величины являются функциями координат 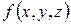, а также могут изменяться во времени 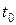, в связи с чем различают:

- установившееся движение жидкости (рис. 23а), при котором скорости, давления и глубины не меняются с течением времени, а зависят только от положения в потоке жидкости рассматриваемой точки, являясь функцией координат:

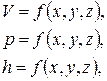
где 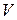− скорость движения;

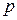− гидродинамическое давление;

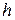− глубина потока.

- неустановившееся движение жидкости (рис. 23б), при котором все перечисленные выше компоненты являются функцией не только координат, но и времени (т. е. изменяются с течением времени):

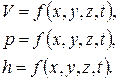
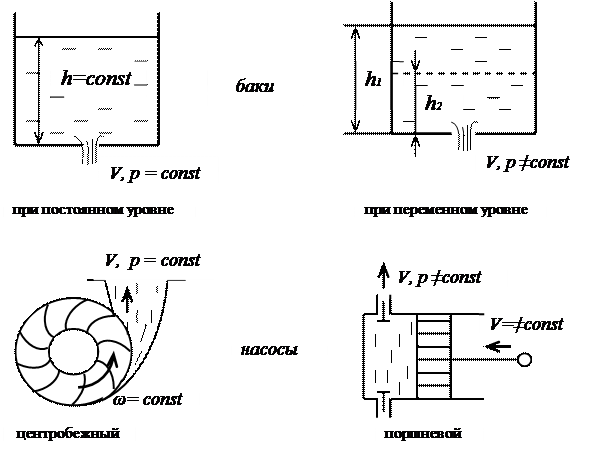а) б)

Рисунок 23 − Примеры установившегося и неустановившегося движения

Установившееся движение в свою очередь подразделяется на равномерное и неравномерное.

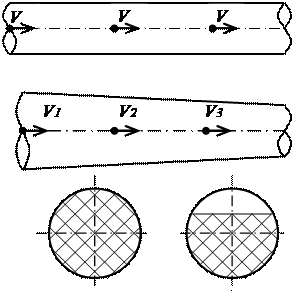Равномерным называется такое установившееся движение, при котором живые сечения вдоль всего потока не изменяются, в этом случае 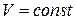и 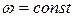(рис. 24).

Неравномерным называется такое движение, при котором распределение скоростей неоди-наково в различных поперечных сечениях; при этом средняя скорость и площадь сечения могут быть и постоянными.

Напорным называется такое движение жидкости, при котором поток полностью заключен в твердые стенки и не имеет свободной поверхности. Движение происходит за счет разности давлений 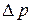и под действием силы тяжести.

Безнапорным называется поток, имеющий свободную поверхность. Движение происходит за счет силы тяжести и начальной скорости.

Еще один вид движения жидкости − свободная струя, не ограниченная твердыми стенками. В этом случае движение жидкости происходит по инерции и под действием силы тяжести.

При рассмотрении движения жидкости пользуются следующими понятиями и определениями:

Линией тока (рис. 25) называется кривая, проведенная в жидкости, касательные к которой в каждой точке совпадают с направлением векторов скоростей частиц, лежащих в данный момент на этой кривой, причем каждая последующая частица расположена на направлении вектора скорости предыдущей.

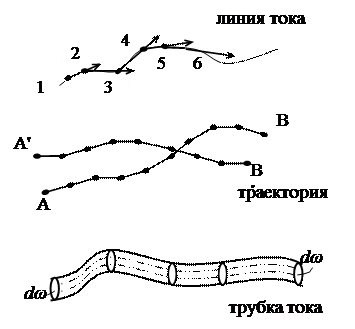Траекторией частицы назы-вается путь, описанный частицей в пространстве.

Выберем в жидкости замкнутый контур и проведем через каждую его точку линию тока, получим трубку тока.

Трубкой тока называется трубчатая поверхность, образо-ванная линиями тока, про-ходящими через все точки конечно малого замкнутого контура, при-чем все его точки принадлежат различным линиям тока.

Жидкость, движущаяся внутри трубки тока, называется элементарной струйкой (элементарная струйка абсолютно непроницаемая).

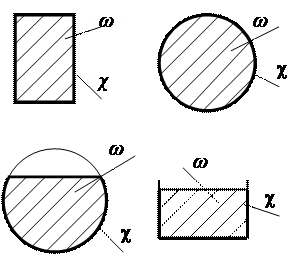Потоком жидкости называется совокупность элементарных струек, текущих в заданных границах.

Живым сечением 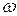называется поверхность, проведенная в границах потока и нормальная ко всем линиям тока (рис. 26).

Смоченным периметром 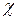называется часть периметра живого сечения, соприкасающегося с ограж-дающими стенками.

Гидравлический диаметр представляет собой отношение учетверенной площади живого сечения к смоченному периметру

.

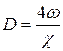Гидравлический радиус − это отношение площади живого сечения к смоченному периметру, он равен 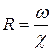и соответственно .

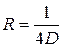Количество жидкости, проходящее через живое сечение в единицу времени, называется расходом. Расход может быть объемным, массовым, весовым.

Объемный: .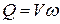

Массовый: .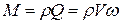

Весовой: ,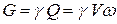

где 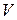− средняя скорость,

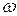− площадь живого сечения,

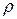− плотность,

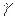− удельный вес.

Так как скорости различных струек реального потока в общем случае различны, то объемный расход всего потока равен:

.

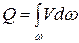Фиктивная скорость, с которой должны двигаться все частицы жидкости для обеспечения расхода 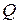, называется средней скоростью.

,

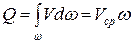откуда ,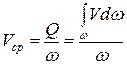

тогда телом расхода, построенным на средней скорости, будет цилиндр с высотой 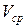и основанием, равным площади сечения потока .

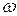Уравнение постоянства расхода (уравнение неразрывности)

Основываясь на законе сохранения вещества, на пред-положении о сплошности тече-ния и на свойстве трубки тока (ее непроницаемости) можно утверждать, что расход во всех сечениях элементарных струек один и тот же (рис. 27).

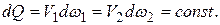
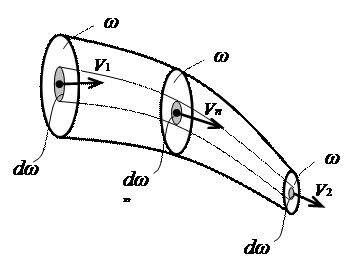
Это и есть уравнение неразрывности (сплошности) для элементарной струйки, которое формулируется так: элементарный расход жидкости при установившемся движении есть величина постоянная для всей элементарной струйки.

Аналогичное уравнение составим и для потока конечных размеров, введя среднюю скорость.

.

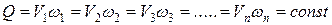Уравнение неразрывности для потока жидкости читается так: расход жидкости через любое сечение потока при установившемся движении есть величина постоянная. Из уравнения неразрывности потока для двух сечений можно написать:

.

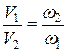Из этого уравнения следует, что средняя скорость обратно пропорциональна площади живого сечения.