Единичная функция хэвисайда. запись оригиналов с помощью функции хэвисайда.
Определение.Единичной функцией Хэвисайда называется функция 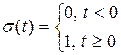 .
.
График этой функции выглядит следующим образом:
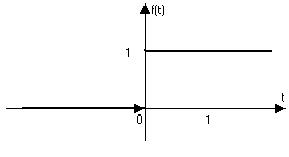 |
С помощью этой функции оригиналы можно записывать в аналитическом виде.
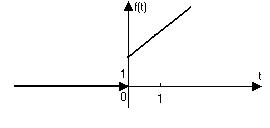
Пример 1. Построить график и записать единым аналитическим выражением 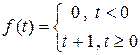 .
.
Решение. 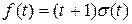
Пример 2. Построить график и записать единым аналитическим выражением 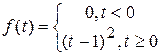
Решение. 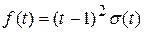
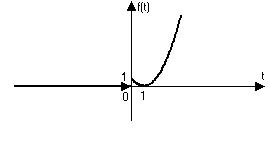
Определение.Смещенной единичной функцией Хэвисайда называется функция 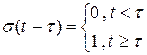 ,
, 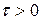 .
.
Число 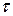 - это “ задержка ” или смещение этой функции.
- это “ задержка ” или смещение этой функции.
График смещённой функции Хэвисайда выглядит следующим образом.
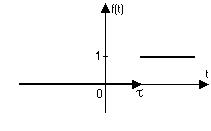
С помощью функции Хэвисайда, любую функцию 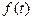 можно “включить с задержкой
можно “включить с задержкой 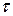 “ путём умножения на
“ путём умножения на 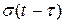 .
.
Пример 3. Построить график и записать единым аналитическим выражением 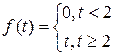 .
.
Решение. 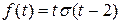
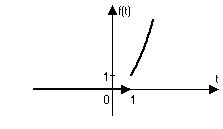
Пример 4. Построить график и записать единым аналитическим выражением 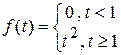 .
.
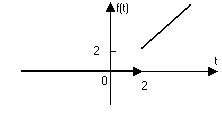
Решение.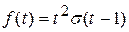
Примеры для самостоятельного решения
Построить графики следующих оригиналов
1) 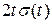 ; 2)
; 2) 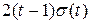 ; 3)
; 3) 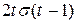 ; 4)
; 4) 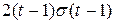
Ответы:
1) 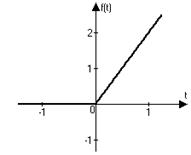 | 2) 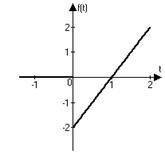 |
3) 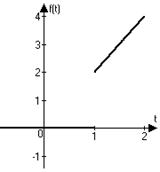 | 4) 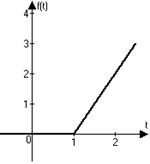 |
Вопросы для самопроверки
1. Дайте определение функции Хевисайда
2. Дайте определение смещенной функции Хевисайда
Преобразование Лапласа. Изображение оригинала. Основные свойства изображения.
Определение.Изображением функции - оригинала 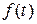 называется функция
называется функция 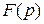 комплексной переменной
комплексной переменной 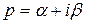 , определяемая формулой
, определяемая формулой 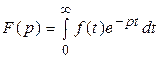 .
.
Интеграл в правой части равенства называется интегралом Лапласа.
Определение.Преобразование, ставящее в соответствие оригиналу 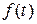 его изображение
его изображение 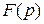 называют преобразованием Лапласа.
называют преобразованием Лапласа.
Теорема. Для всякого оригинала 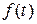 существует изображение
существует изображение 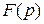 , определённое в полуплоскости
, определённое в полуплоскости 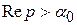 , где
, где 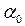 — показатель роста
— показатель роста 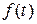 , причём связь между
, причём связь между 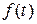 и
и 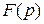 является взаимно – однозначной.
является взаимно – однозначной.
Соответствие изображения 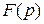 оригиналу
оригиналу 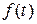 можно обозначать следующим образом:
можно обозначать следующим образом: 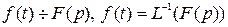 , а соответствие оригинала
, а соответствие оригинала 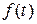 изображению
изображению 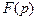 таким образом:
таким образом: 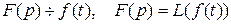 .
.
Пример 1. Найти изображение функции Хэвисайда 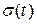 :
:
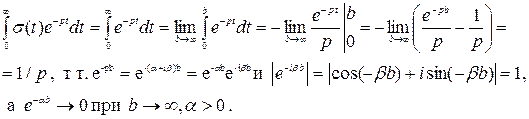
Таким образом 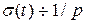 , если
, если 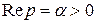 .
.
Перечислим основные свойства преобразования Лапласа.
Свойство линейности.
Если 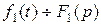 , а
, а 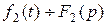 , то при любых
, то при любых 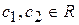
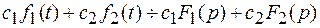 .
.
Свойство затухания.
Если 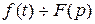 , то
, то 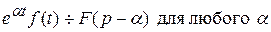 .
.
Свойство подобия.
Если 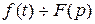 , то
, то 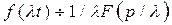 для любого
для любого 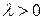 .
.
С помощью основных свойств преобразования Лапласа и найденного ранее изображения функции 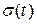 , получим изображения следующих оригиналов :
, получим изображения следующих оригиналов : 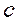 ,
, 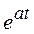 ,
, 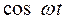 ,
, 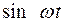 ,
, 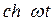 ,
, 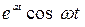 ,
, 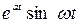 ,
, 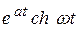 ,
, 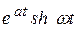 , которые затем поместим в таблицу.
, которые затем поместим в таблицу.
Найдем изображение константы с.
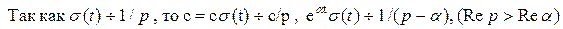 .
.
Далее воспользуемся формулами Эйлера, чтобы найти изображение остальных функций:
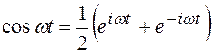 , , | 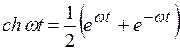 , , |
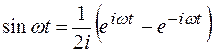 , , | 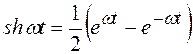 ; ; |
Используя свойства затухания и линейности получаем :
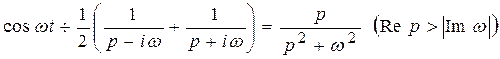 ;
;
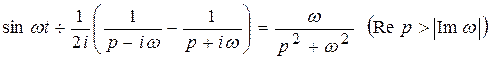 ;
;
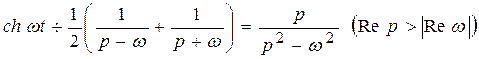 ;
;
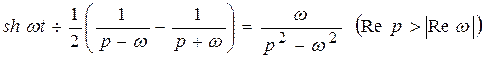 .
.
Применяя свойство затухания, получаем:
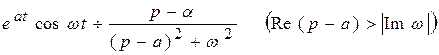 ;
;

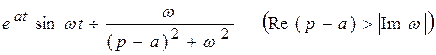 ;
;
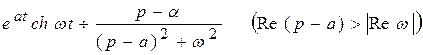 ;
;
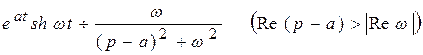 .
.
Примеры 1-4.Найти изображение следующих оригиналов
1) 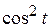 ; ; | 2) 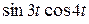 ; ; | 3) 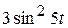 ; ; | 4) 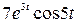 |
Решение.
Сначала оригиналы приводим к табличному виду, а затем находим их изображения:
1) 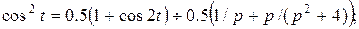
2) 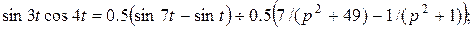
3) 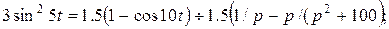
4) 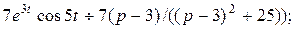
Вопросы для самопроверки
1. Дайте определение изображения
2. Сформулируйте теорему линейности
3. Сформулируйте теорему подобия
4. Сформулируйте теорему затухания
