Четырехмерные векторы и тензоры. Четырехмерные скорость и ускорение

Будем называть четырехмерным радиус-вектором 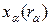; 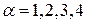, вектор с компонентами .

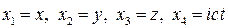При поворотах в четырехмерном пространстве компоненты этого вектора

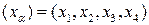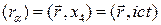, или (1)

преобразуются по закону

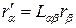, (2)

причем остается постоянным. Последнее означает, что матрица преобразования Лоренца ортогональная, т.е.

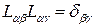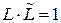, или , (3)

Действительно,

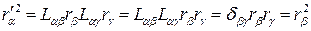, (4)

В частном случае движения систем отсчета, когда одноименные координаты ИСО параллельны, относительная скорость направлена вдоль z, и начала координат при 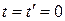совпадали, матрица преобразований Лоренца имеет вид

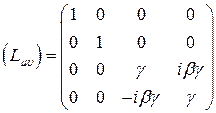, (5)

В общем случае произвольного направления скорости относительного движения 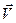преобразование типа (2) можно записать в блочно-матричном виде

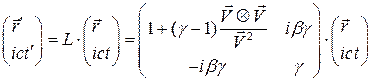, (6)

По аналогии с 4-радиус-вектором любой набор заданных в каждый из ИСО упорядоченных чисел 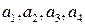называют 4-вектором и обозначают 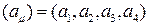, если при переходе от одной ИСО к другой они преобразуются по формулам

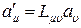; или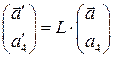

Трехмерный вектор 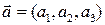называют пространственнй частью 4-вектора, а величину 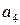по аналогии с четвертой компонентой четырехмерного радиус-вектора - временной составляющей 4-вектора.

Для четырехмерных векторов, как и для трехмерных, можно ввести понятие скалярного произведения

.

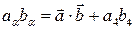Векторы 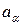и 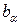называются ортогональными, если .

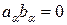Важной характеристикой 4-вектора является его квадрат

.

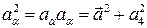Это инвариант, так как

,

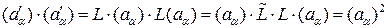или в координатной форме записи

.

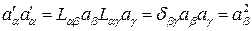Квадрат 4-вектора не является существенно положительным. Если 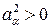, то вектор называется пространственноподобным; а если 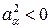, то вектор называется времениподобным.

Введем два важных 4-вектора: скорости и ускорения.

Необходимо построить 4-вектор скорости так, чтобы он был производной от 4-х мерного радиус-вектора по некоторому инварианту (скаляру). Этот скаляр должен быть таким, чтобы при 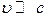пространственные компоненты скорости превращались в компоненты обычной скорости.

Поэтому естественно определить 4-вектор скорости соотношением

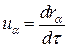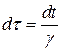; , (7)

.

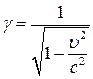Подчеркнем, что 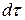в (7) – интервал собственного времени, то есть времени в мгновенно сопутствующей частице системе и, значит, 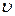, , 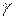вообще говоря, переменные величины - функции времени.

Для компонент 4-скрости имеем

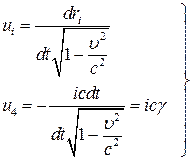, (8)

Квадрат 4-вектора скорости

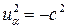, (9)

т.е - он является временеподобным вектором.

Определим 4-вектор ускорения как

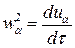
Для компонент вектора ускорения получим:

.

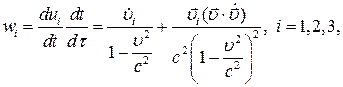
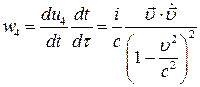Легко убедиться, что , а это означает, что 4-вектор ускорения является пространственно подобным.

Дифференцируя (9) по , находим, что 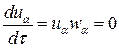, т.е. векторы скорости и ускорения всегда ортогональны.

Наряду с определением 4-вектора можно ввести понятие 4-тензора второго ранга как упорядоченной совокупности заданных в любых ИСО 16 величин 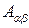, которые преобразуются следующим образом

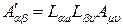или 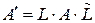.