Общая схема исследования функции

И построение ее графика

В различных учебниках рекомендуются общие схемы исследования функции, отличающиеся лишь в деталях. Можно предложить следующий план исследования.

1. Найти область определения функции.

2. Найти точки разрыва (если они есть) и определить их род.

3. Определить четность, нечетность, периодичность функции.

4. Найти точки экстремума и интервалы монотонности (эти два элемента поведения функции определяются, как правило, одновременно).

5. Найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.

6. Найти асимптоты графика функции.

7. Для получения графика функции в некоторых случаях полезно найти несколько точек (например, точки пересечения с осями координат), определить поведение функции при .

На основании исследования функции нетрудно построить ее график. При его построении рекомендуется сначала нанести на координатную плоскость найденные точки графика и изобразить график в окрестности точек экстремума.

Пример. Исследовать функцию и построить ее график.

Решение.

1. Функция определена во всех точках, кроме 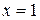, т.е. область определения составляет множество .

2. В точке 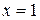функция разрывна. В остальных точках функция непрерывна.

3. Условия четности и нечетности не выполняются

,

.

Функция не является ни четной, ни нечетной. Это функция общего вида. Следовательно, график функции не симметричен ни относительно оси , ни относительно начала координат. Функция непериодическая (что очевидно).

4. Найдем экстремум функции и интервалы монотонности:

.

: ; . Отсюда , .

Производная не существует в точке 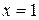, но в этой точке не существует и сама функция.

Исследуем критические точки:

	-		-	-		+
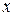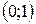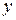		нет экстр			min

Из таблицы находим интервалы монотонности функции: если функция убывает, если – функция возрастает. При .

5. Находим вторую производную

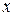: ; , при любых значениях . Тогда решением является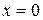

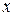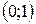	+	перегиб	-	не существует	+

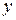График функции является вогнутым на интервалах и , выпуклым на интервале .

В точке 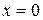функция имеет перегиб; .

6. Найдем асимптоты:

а) вертикальная ;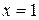

б) проверим наличие наклонных асимптот :

.

Отсюда следует, что наклонных асимптот нет.

7. График пересекает оси координат в точке . При .

Построим график (рис. 9).

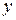
0 1 3/2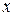

Рис. 9

4. Неопределенный интеграл

4.1. Первообразная функция и неопределенный интеграл

Основной задачей дифференциального исчисления является определение для заданной функции ее производной или ее дифференциала .

Обратная задача, состоящая в определении функции по ее известным производной 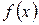или дифференциалу , представляет собой основную задачу интегрального исчисления.

Определение.

Первообразной функцией функции , определенной на некотором промежутке, называется функция , существующая на том же промежутке и удовлетворяющая условию или .

Процесс нахождения первообразной функции для заданной функции называется ее интегрированием.

Если функция является первообразной для функции 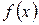, то и функция , где – производная постоянная величина, также является первообразной функции 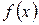. Таким образом, если функция 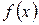имеет первообразную, то она имеет их бесчисленное множество, причем все они отличаются одна от другой только постоянным слагаемым.

Определение.

Неопределенным интегралом от функции называется совокупность всех ее первообразных и обозначается: .

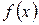Здесь знак интеграла, – подынтегральная функция, – подынтегральное выражение, 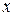– переменная интегрирования, – произвольная постоянная величина.

Основные свойства неопределенного интеграла

1о	Постоянный множитель можно выносить за знак интеграла .
2о	Неопределенный интеграл от дифференциала функции равен сумме этой функции и произвольной постоянной .
3о	Производная от неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению а) ; б) .
4о	Неопределенный интеграл от алгебраической суммы конечного числа функций равен такой же алгебраической сумме неопределенных интегралов от слагаемых функций .

Таблица основных интегралов

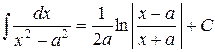К основным методам интегрирования относятся: непосредственное интегрирование, метод замены переменной и интегрирование по частям.