Приближенные методы вычисления определенных интегралов

Пусть функция 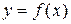непрерывна на отрезке 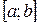. Если она задана аналитически и ее первообразная F(x) на этом отрезке выражается в элементарных функциях, то вычисление определенного интеграла 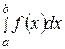сводится к применению формулы Ньютона-Лейбница: .

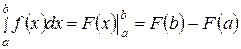Но не для всякой непрерывной функции ее первообразная выражается через элементарные функции (имеются ввиду так называемые «неберущиеся интегралы», например: 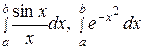и т.д.). Кроме того, на практике сталкиваются с необходимостью вычислять интегралы от функций, заданных табличным или графическим способами, а также интегралы от функций, первообразные которых выражаются через элементарные функции очень сложно что требует большой вычислительной работы и с практической точки зрения не рационально. В этих случаях применяются приближенные методы интегрирования.

Основная идея этих методов состоит в том, что подынтегральную функцию f(х) заменяют другой, «близкой» к ней функцией, первообразная которой находится элементарным способом.

Геометрически это означает, что криволинейную трапецию с основанием 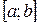, ограниченную сверху кривой 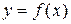, заменяют другой фигурой с тем же основанием, площадь которой близка к искомой площади криволинейной трапеции, но вычисляется гораздо проще. Сама кривая заменяется вписанной в нее ломаной или кривой.

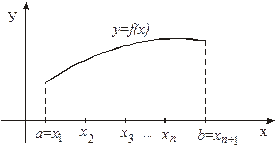Пусть на отрезке 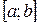, где a < b

задана непрерывная функция f(x).

Требуется вычислить .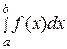

Для наглядности будем считать,

что 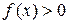на отрезке .

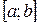Разобьем отрезок 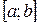на n рав-

ных частей точками :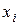

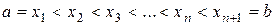. Рисунок 28

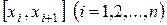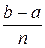Длина h каждого из полученных отрезков равна , т.е. 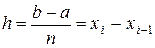(шаг разбиения) (рисунок 28). Обозначим через значения функции f(х) в точках , т.е. ; ; ; .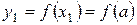

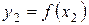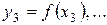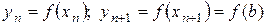В зависимости от того, как аппроксимируют (заменяют) данную функцию 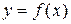на каждом из отрезков 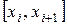, получают различные формулы для вычисления интеграла 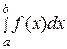. Мы рассмотрим наиболее простые и широко применяемые формулы прямоугольников, трапеций и парабол (Симпсона).

Формулы прямоугольников

При вычислении интеграла 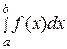по формулам прямоугольников подынтегральная функция заменяется «ступенчатой функцией», которая на каждом из отрезков 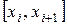имеет постоянное значение, равное значению функции на одном из концов этого отрезка.

Пусть, например, на каждом из

отрезков ступенчатая функция

принимает значения, равные значению

функции f(х) на левом конце этого отрез-

ка, т.е. равные .

Тогда площадь криволинейной трапе-

ции заменяется площадью ступенчатой

фигуры (рисунок 29) и считается прибли- Рисунок 29

женно равной сумме площадей прямоугольников с высотами 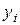и основаниями 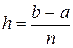. 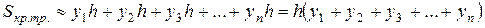, т.е.

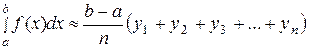. (47)

Если же значения ступенчатой функции

на каждом из отрезков совпадают

со значениями функции у=f(х) на правых

концах этих отрезков (рисунок 30), то полу-

чаем формулу:

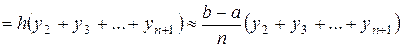. Рисунок 30

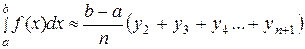. (48)

Формулы (47) и (48) называются формулами прямоугольников.

Чем меньше шаг разбиения (т.е. чем больше n), тем площадь ступенчатой фигуры ближе к площади криволинейной трапеции, т.е. формулы (47) и (48) тем точнее, чем больше n. Иногда, в целях уточнения результата, за величину 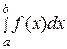принимают среднее арифметическое значений, полученных по формулам (47) и (48).

Погрешность этих формул может быть оценена следующим образом:

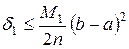, где 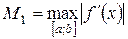. (49)

Замечание. Если функция на отрезке возрастает, то формула (47) дает приближенное значение интеграла с недостатком, а формула (48) – с избытком. Для убывающей функции f(х) все наоборот.

Формула трапеций

Подынтегральную функцию

f(x) заменим функцией, представ-

ляющей собой ломаную линию,

звенья которой соединяют концы

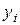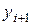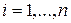ординат и , (ри-

сунок 31). В этом случае площадь

криволинейной трапеции (а, сле-

довательно, и значение искомого Рисунок 31

интеграла) считается приближенно равной сумме площадей обычных трапеций с основаниям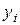и и 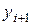и высотой h.

.

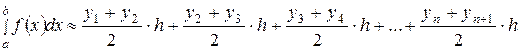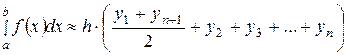. (50)

Формула (50) называется формулой трапеций.

Погрешность этой формулы может быть оценена следующим образом:

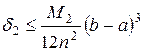, где 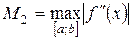. (51)

Формула Симпсона

Этот метод приближенного вычисления определенного интеграла основан на замене графика подынтегральной функции не хордами, как в методе трапеций, а дугами парабол, оси которых параллельны оси Оу.

Рассмотрим сначала частный случай, когда кривая, ограничивающая криволинейную трапецию, является параболой, определяемой уравнением 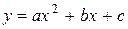на отрезке .

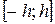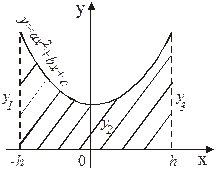
Найдем площадь такой криволинейной трапеции (рисунок 32).

.

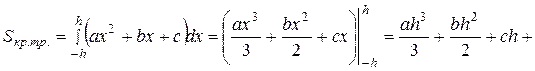
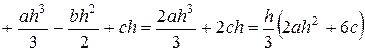Определим значения: ,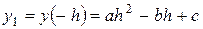

, .

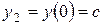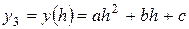Умножим второе уравнение на 4 и сложим

все уравнения: .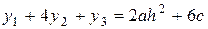

Сравнивая выражение для площади

криволинейной трапеции и полученное ра- Рисунок 32

венство, имеем, что:

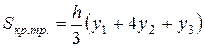, (52)

Формула (52) называется малой формулой Симпсона.

Сдвинем параболу вдоль оси Ох (рисунок 33) так, что 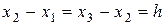. В этом случае малая формула Симпсона остается справедливой, так как при параллельном пере-

носе кривой величины 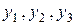и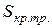

не изменяются.

Можно доказать, что коэффициенты

а, b, с, входящие в уравнение параболы

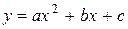определяются однозначно,

в силу того, что через любые три точки плос-

кости , ,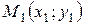

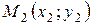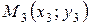
можно провести параболу и притом только одну. Рисунок 33

Вернемся теперь к криволинейной трапеции, площадь которой задана интегралом 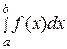. Разобьем отрезок 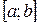на четное число равных частей.

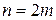- четное, .

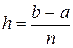Объединив полученные части попарно, заменим каждую криволинейную трапецию с основанием 2h такой, которая сверху ограничена не кривой 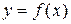, а параболой, проведенной через соответствующие три точки этой кривой: 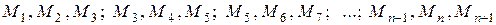(рисунок 34).

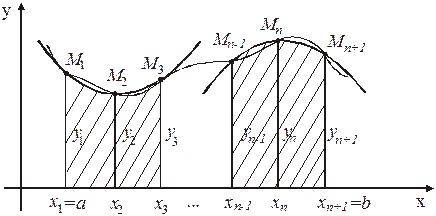
Рисунок 34

Площадь каждой такой трапеции с основанием 2h вычислим по малой формуле Симпсона (52), а площадь всей криволинейной трапеции приближенно равна их сумме: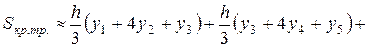

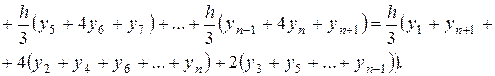
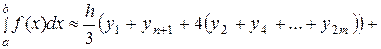
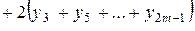
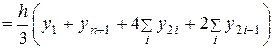. (53)

Формула (53) называется формулой Симпсона, а ее погрешность можно оценить так:

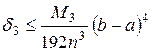, где 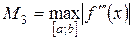. (54)

Пример 18. Вычислить интеграл с точностью до 0,001 сначала по формуле Ньютона-Лейбница, а затем найти приближенное значение по формулам прямоугольников, трапеций, Симпсона, разбив отрезок интегрирования на 10 равных частей. Все промежуточные вычисления производить с округлением до четвертого десятичного знака. Сравнить полученные результаты с точным значением интеграла, найдя абсолютную и относительную погрешности для каждой из формул; сделать выводы.

Решение. 1) Вычислим данный интеграл по формуле Ньютона-Лейбница:

.

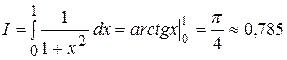2) Для вычисления интеграла по приближенным формулам составим таблицу 1 значений подынтегральной функции для n = 10, 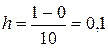; 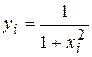, выделяя в ней столбцы значений функции с четными и нечетными индексами.

Таблица 1 – Значения подынтегральной функции .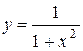

i	хi	у1, у11	уi,(i- четн.)	уi, (i – нечетн.)
		1,0000
	0,1		0,9901
	0,2			0,9615
	0,3		0,9174
	0,4			0,8621
	0,5		0,8000
	0,6			0,7363
	0,7		0,6711
	0,8			0,6098
	0,9		0,5525
	1,0	0,5000
∑		1,5000	Sчет = 3,9311	Sнеч = 3,1687

Вычислим приближенное значение интеграла по формулам прямоугольников. Для удобства вычислений формулу прямоугольников (47) перепишем в виде: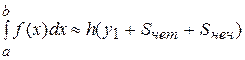

Так как подынтегральная функция убывает на [0; 1], то, используя эту формулу, мы получим приближенное значение интеграла с избытком:

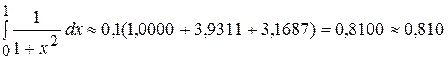
Абсолютная погрешность ∆ вычислений определяется как разность между точным и приближенным значениями интеграла, взятая по абсолютной величине: 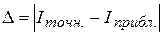(55)

Тогда .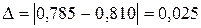

Относительная погрешность δ определяется как отношение абсолютной погрешности к точному значению интеграла в процентах:

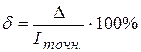(56)

.

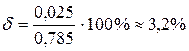Формулу прямоугольников (48) запишем в виде:

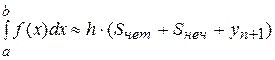
Тогда, 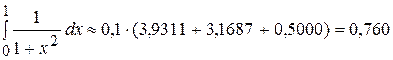- приближенное значение интеграла с недостатком.

Абсолютная погрешность: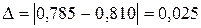

Относительная погрешность: .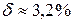

Для получения более точного значения данного интеграла можно взять среднее арифметическое значений, полученных по формулам прямоугольников: .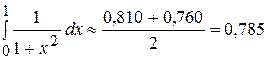

Вычислим приближенное значение интеграла, используя формулу трапеций. Формулу трапеций (48) перепишем в виде:

.

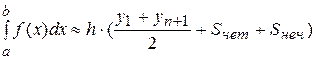Тогда для данного интеграла

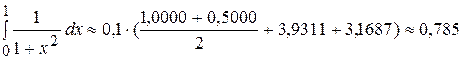
Абсолютная и относительная погрешности равны нулю. Вычислим приближенное значение интеграла по формуле Симпсона.

Формулу Симпсона (53) запишем в виде:

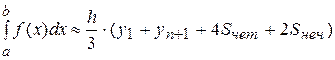
Тогда для данного интеграла

.

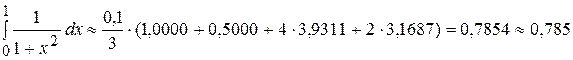Абсолютная и относительная погрешности равны нулю. Сравнивая полученные результаты, замечаем, что формулы трапеций и Симпсона дают наибольшее приближение к точному значению интеграла.